大步長路徑跟蹤內點新算法

周廣付， 姚奕榮， 王筱莉

(上海大學理學院，上海200444)

在過去的20年里，內點法的研究一直是非線性規劃及最優化領域最引人注目的熱點［1-3］.內點法已廣泛應用于經濟金融、工程控制、技術物理、物流配送、計算機科學及生物工程等領域，但是在實際的理論研究、測試及收斂性證明中也遇到了一些問題：①對于初始點的選取，內點法的核心思想是從問題的可行域中的某一點出發，沿著中心路徑進行搜索，最后到達問題的最優解.但是，對于一些具有多個約束的大規模問題，一個初始可行點的選取是很困難的.在線性規劃問題中，可采用一些非可行內點法來克服這一困難［4-9］，但這些方法對于一般的非線性規劃問題不能得出令人滿意的結果.在錐優化模型中，文獻［10］提出了把自對偶嵌入技術推廣到隨機動態規劃及更一般的錐優化問題中，從而使初始化難題得到解決.本工作通過引入一個輔助變量并在迭代過程中使該輔助變量的值逐步趨近于零，較好地解決了路徑跟蹤內點算法初始點選取的難題.②對于收斂性的證明，路徑跟蹤內點算法作為原對偶內點算法的延伸和擴展，憑借其良好的全局收斂性和較低的時間復雜度，一直受到人們的廣泛關注.但對迭代方向正交性的要求，已成為路徑跟蹤內點算法運用于求解非線性規劃問題的一道障礙.通過對算法的研究和測試，本工作提出了一個新的關系不等式，并證明了該算法的全局收斂性.因此，本工作使路徑跟蹤內點法的應用得以拓展.

1 KKT條件

首先，考慮如下約束優化問題：

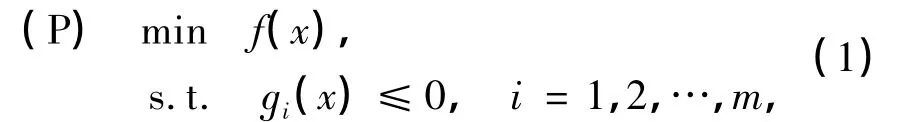
式中，f，ɡi：Rn→R(i=1，2，…，m)是二次連續可微的.

引入變量x0，則問題(P)轉化為

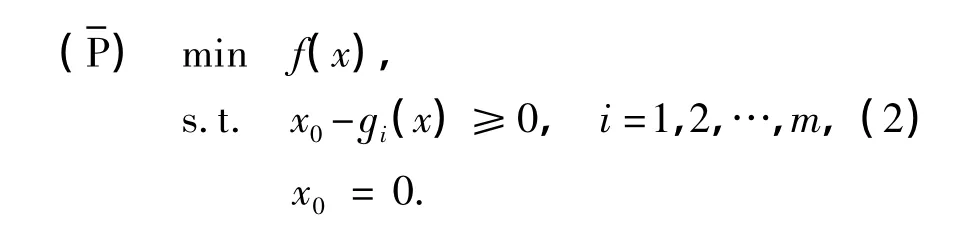
定義該問題的拉格朗日函數為

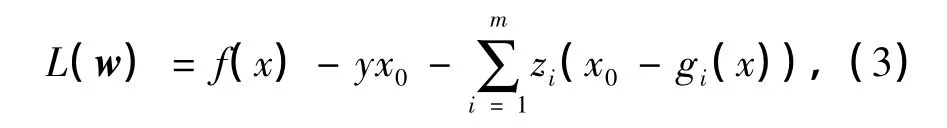
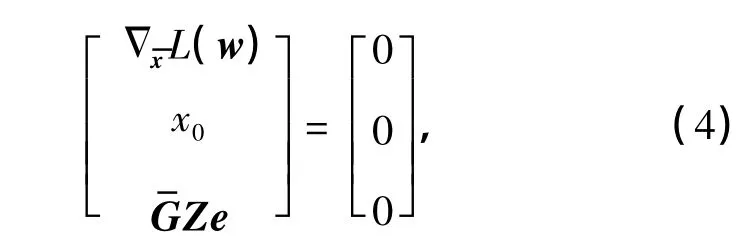
式中，

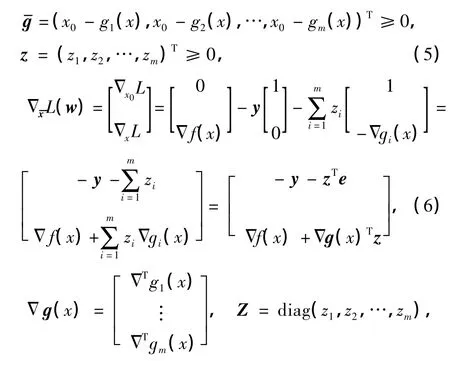
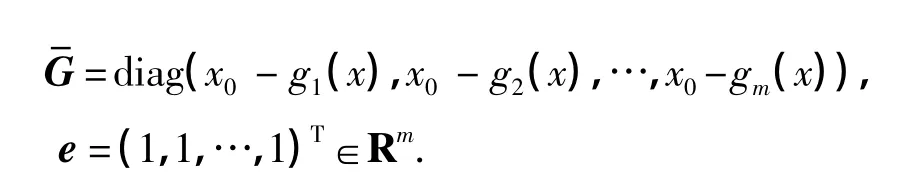
對KKT條件引入松弛變量s=(s1，s2，…，sm)T，可得到式(4)的等價形式為

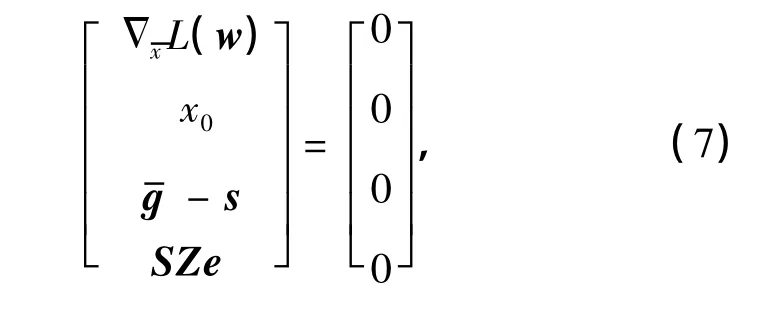
式中，s，z≥0，S=diag(s1，s2，…，sm).

在實際求解過程中，通常采用Newton法來求解上述KKT條件等式，那么Newton方程的解即為Newton迭代方向Δw=(Δx-，Δs，Δy，Δz)T，有

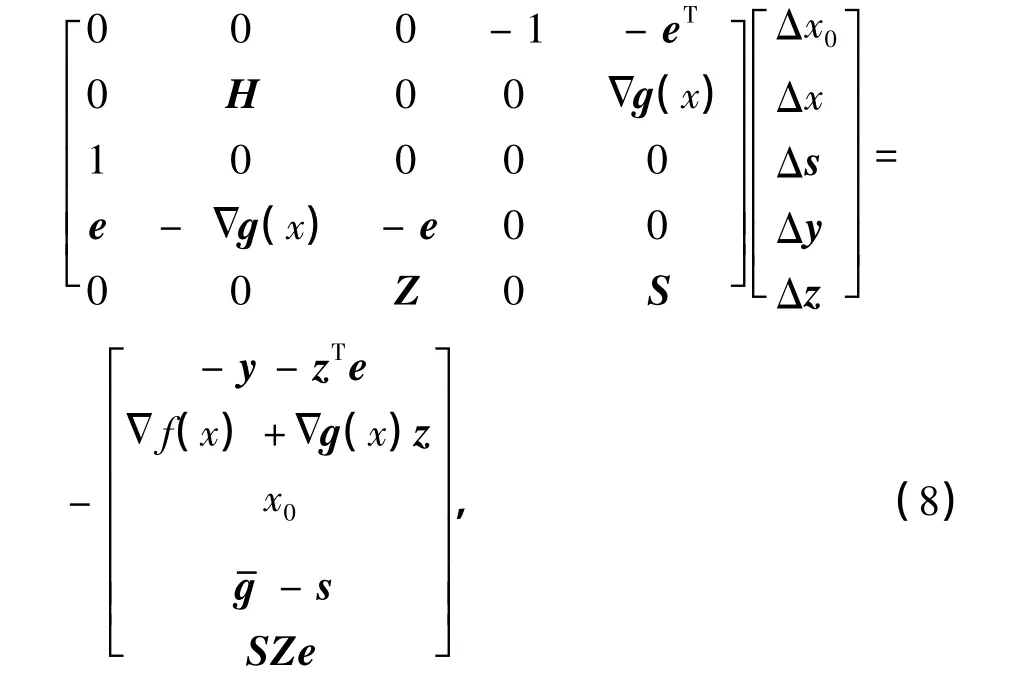
2 路徑跟蹤內點算法

中心路徑在內點算法中扮演著非常重要的角色，它是由一類嚴格可行點組成的弧形軌跡.若有參數τ＞0，則中心路徑中的點可通過下列方程式進行求解：

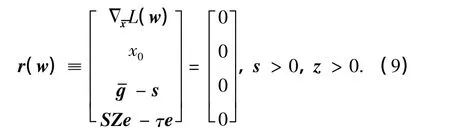
本工作稱條件(9)為修正的KKT條件.條件(9)與條件(7)之間唯一的差別在于，條件(9)在最后一行中引入了參數τ，即把條件(7)第三行中的互補條件換成了要求sizi乘積值對任意下標i均相等的條件.由條件(9)可定義中心路徑C={(，sτ，yτ，zτ)| τ＞0}.當τ趨近于0時，條件(9)等價于條件(7);當τ下降到0時，C收斂于某一點，那么該點必為原問題的最優點.因此，沿著中心路徑搜索的方法提供了一條找到最優解的途徑，沿著該途徑不僅可以保證s和z各個分量都嚴格大于0，還可以使所有sizi的乘積值幾乎以相同的速率下降到0.

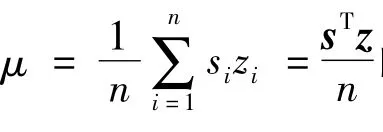
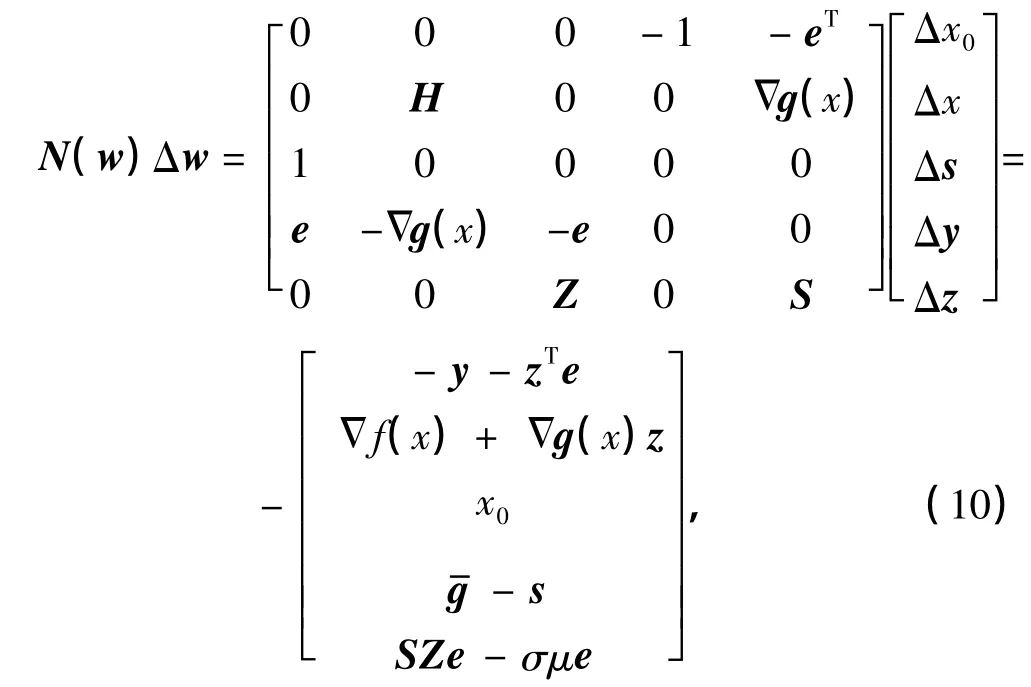
當sizi的各個分量均等于σμ時，Newton迭代方向(Δ，Δs，Δy，Δz)指向點(，sσμ，yσμ，zσμ)∈C;反之，由式(8)求得的迭代方向則直接指向滿足KKT條件(7)的點.

下面，給出式(10)可解的充分條件.

引理1 如果矩陣H+ΔgT(x)S-1ZΔg(x)是正定的，則矩陣N(w)非奇異.

證明 考慮方程式

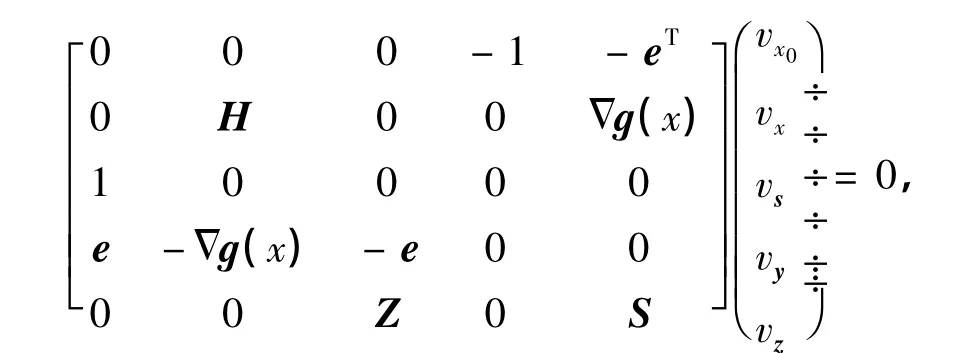
式中，(vx0，vx，vs，vy，vz)∈R1×Rn×Rm×R1×Rm，則有

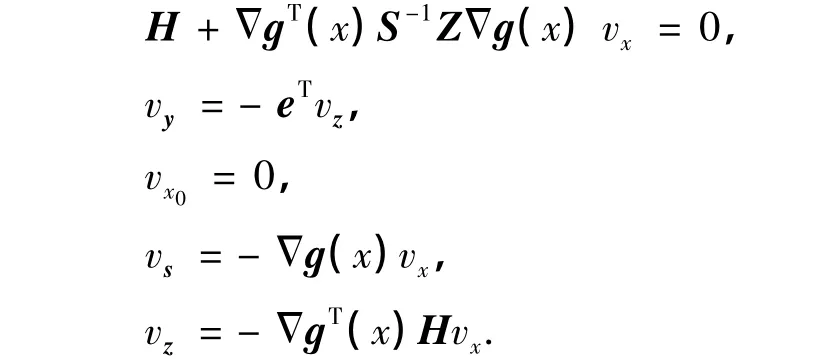
由假設知，vx=0，因此，vx0=0，vs=0，vy=0，vz=0.由此，可求得(Δ，Δs，Δy，Δz)T.證畢.

路徑跟蹤算法要求每步產生的迭代點均落在一個包含中心路徑C的區域內，且沿著這條中心路徑可搜索至原問題的最優解.為了避免迭代點過于接近非負區域的邊界，本工作要求每次迭代中的搜索方向必須使下一步產生的點列更加接近最優點.

最優性算法的一個要點是如何在搜索空間中衡量滿足條件的點，因此，在路徑跟蹤算法中，對偶參數μ擔當了這個重要的角色.當k→∞時，μk下降至0，因此，迭代點(k，sk，yk，zk)逐步滿足KKT條件(7).

現定義單邊∞范數區域N-∞(γ)如下：

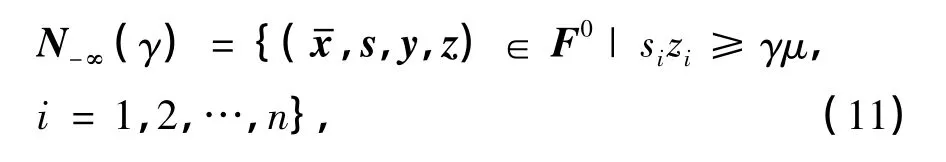
式中，γ∈(0，1］，F0={(，s，y，z)|s＞0}.若存在一點落在N-∞(γ)中，則對每個分量sizi必定大于μ與γ的乘積.這個約束是非常松的，當γ→0時，N-∞(γ)就包含可行域F={(，s，y，z)|s≥0}中的大部分點.本工作取γ=10-3.

下面介紹的大步長路徑跟蹤算法，由于采用了一個較為廣泛的區域N-∞(γ)(γ→0)，因此，該算法具有良好的實用性.通過式(10)可求得搜索方向，步長αk則取保證迭代點落于N-∞(γ)內的最大值.

定義

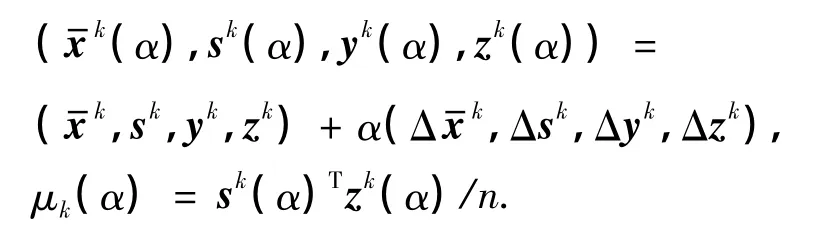
大步長路徑跟蹤內點算法步驟如下：

(1)給定 ε＞0，γ，σ∈(0，1)，取 x0及＞max(ɡi(x0))，s0=0，y0和z0;

(2)如果‖r(wk)‖≤ε，停止;

(4)取αk作為α在區間［0，1］中的最大值，且有((αk)，sk(αk)，yk(αk)，zk(αk))∈N-∞(γ);

(6)令k∶=k+1，轉步驟(1).

3 收斂性分析

下面部分分析上述算法的收斂性.首先，介紹引理2［4］，并用它來證明引理3.引理3給出了ΔiΔzi(i=1，2，…，n)向量乘積的邊界.定理1給出了αk的一個下確界以及迭代過程中測度μ下降量的估計值，由此即可得算法的全局收斂性.為了證明算法的收斂性，給出如下假設：

(1)矩陣H+ΔɡT(x)S-1ZΔɡ(x)正定;

(2)不等式0≤ΔsTΔz≤(1-σ)sTz成立.

引理2 假設u，v是任意2個n維向量，且有uTv≥0，那么

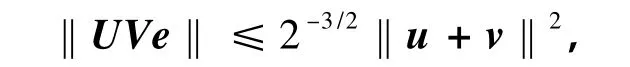
式中，U=diag(u1，u2，…，un)，V=diag(v1，v2，…，vn).

證明 由假設(2)，易得

把式(10)的最后一行兩邊分別乘以(SZ)-1/2，并令D=S1/2Z-1/2，可得

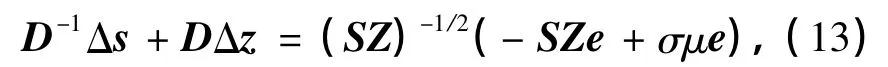
因為

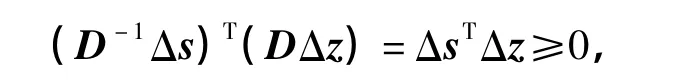
令u=D-1Δs，v=DΔz，由引理2，得

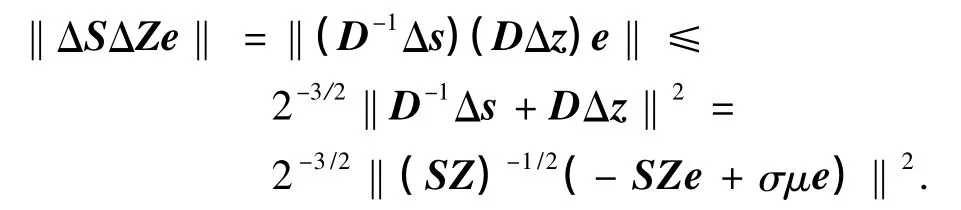
利用展開平方歐氏范數和關系式 sTz=nμ，eTe=n，有

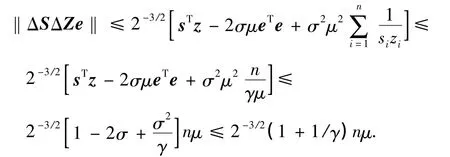
證畢.

定理1 由假設(1)和(2)，給定參數γ，σ∈(0，1)，則存在一個常數δ∈(0，1)，使得

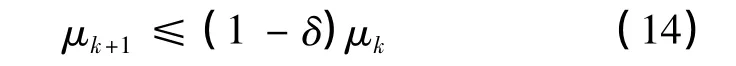
對所有的k≥0成立.

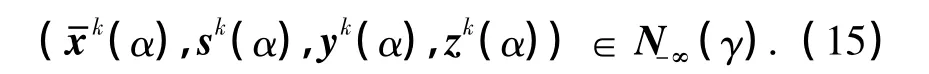
由于αk是［0，1］區間內α的最大值，那么αk有下確界

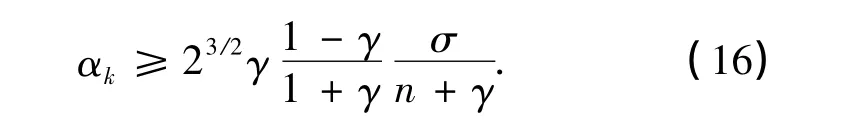
由引理3可知，對任意的i=1，2，…，n，有

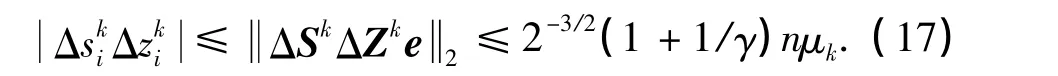
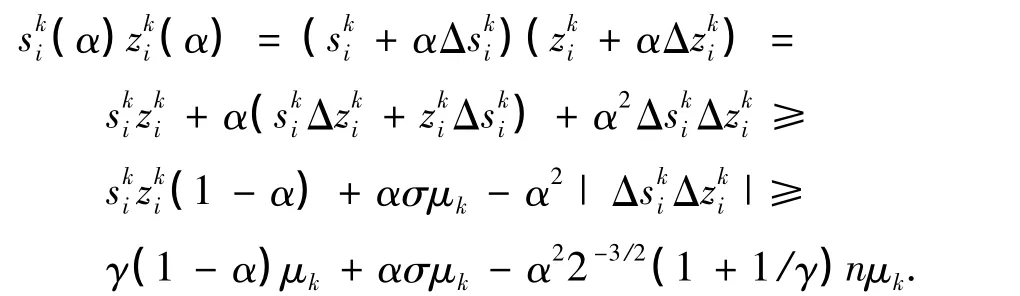
累加方程SkΔzk+ZkΔsk=-SkZke+σμke(由式(10)的最后一行求得)的n個分量，利用式(17)和μk，μk(α)的定義，即得

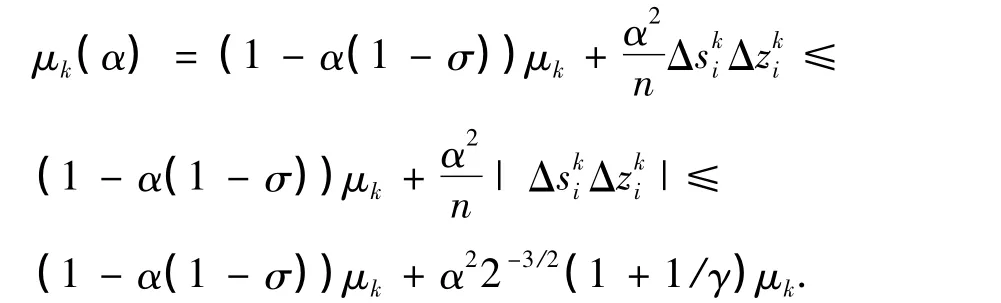
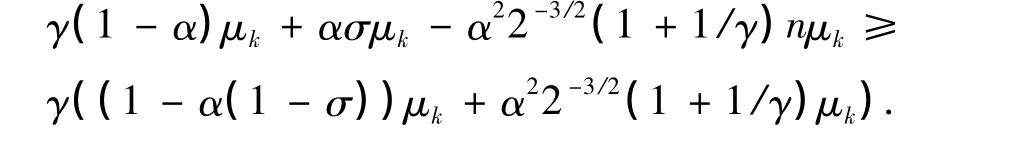
整理上式，可得

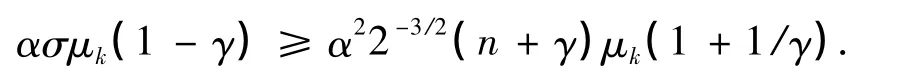
接下來，估計在第k步迭代中測度μ的下降量.由式(10)，(16)，(17)的最后一行以及假設，可得

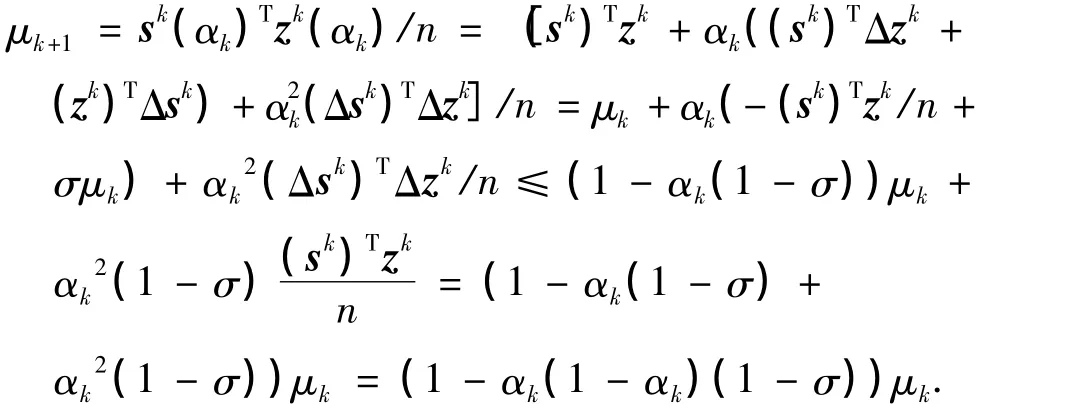
由此可知，α(1-α)是一個關于α的二次凹函數，并且，在任意給定的區間范圍內，函數的最小值可在區間的端點處取到.所以，在最后一式中引入替代估計參數

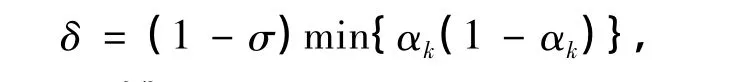
4 數值試驗

本工作測試了3個數值算例，結果表明，所提出的大步長路徑跟蹤內點算法是可行的.

例1

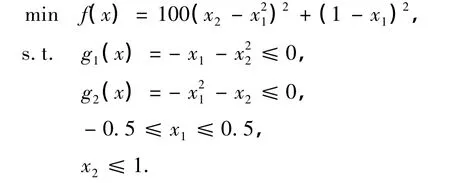
例2

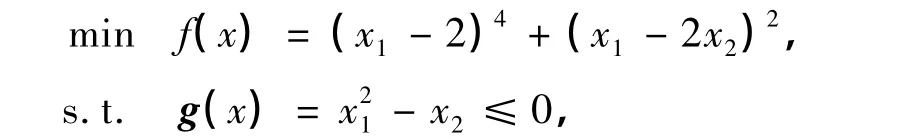
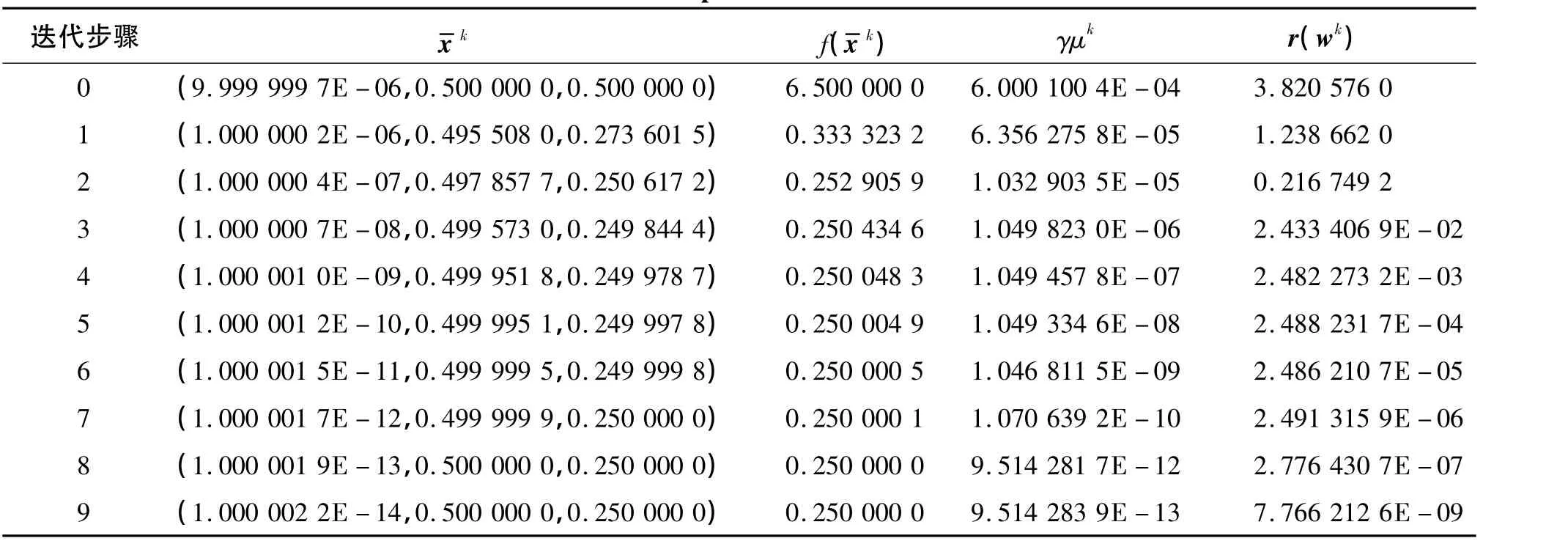
表1 算法迭代9步Table 1 Computations 9 iterations

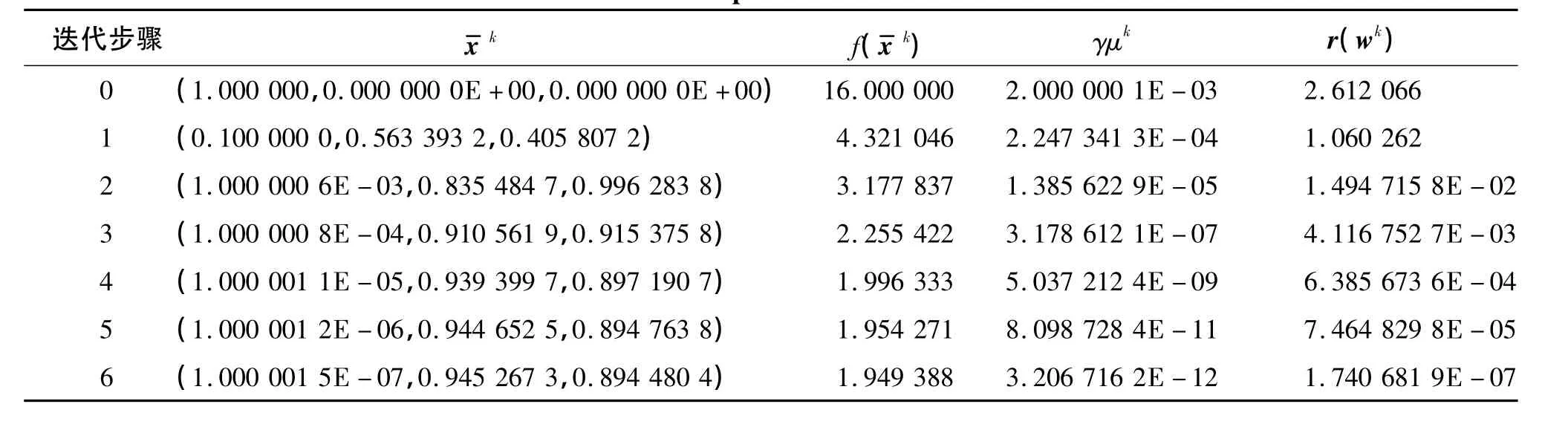
表2 算法迭代6步Table 2 Computations 6 iterations

［1］ BOY，QINGX，FENGG C.On the complexity of a combined homotopy interior method for convex programming［J］.Journal of Computational and Applied Mathematics，2007，200：32-46.

［2］ GEORG S.Path-following and augmented lagrangian methods for contact problems in linear elasticity［J］.Journal of Computational and Applied Mathematics，2007，203：533-547.

［3］ RENATOD C M，TAKASHIT.A strong bound on the integral of the central path curvature and its relationship with the iteration-complexity of primal-dual path-following LP algorithms［J］.Mathematical Programming，2008，115：105-149.

［4］ JORGEN，WRIGHTS J.Numerical optimization［M］.Boston：Springer，1999：60-112.

［5］ JIMB，SONGX.A non-interior predictor-corrector path following algorithm for the monotone linear complementarity problem ［J］. Mathematical Programming，2000，87：113-130.

［6］ BURKEJ，XUS.Complexity of a noninterior pathfollowing method for the linear complementarity problem［J］.Journal of Optimization Theory and Applications，2002，112：53-76.

［7］ FREUNDR M.A potential-function reduction algorithm for solving a linear program directly from an infeasible warm start［J］.Mathematical Programming，1991，52：441-466.

［8］ FORSGRENA.On warm starts for interior methods［M］.Boston：Springer，2006：51-66.

［9］ CORNELISR，TAMáST，JEAN-PHILIIPE V.Interior point methods for linear optimization［M］.Boston：Springer，2006：55-76.

［10］ ZHANGS Z.A new self-dual embedding method for convex programming ［J］. Journal of Global Optimization，2004，29：479-496.