德布羅意物質波和玻恩對波函數的統計解釋
薛立范
包頭輕工職業技術學院,內蒙古包頭 014035
德布羅意在愛因斯坦的光子學說的啟示下,通過對幾何光學和經典力學的對比,大膽的提出了物質波的假設,促進了物理學的發展。
1 德布羅意物質波假設
20世紀20年代前后,有關原子結構和量子理論的研究引起了當時很多物理學家的關注。愛因斯坦的光量子理論通過密立根、康普頓等人的研究得到了證實,德布羅意對此發生了很大的興趣,他認為在對光的研究過程中,同時引進了粒子概念和周期性概念,光本身必須同時考慮粒子性和波動性。他進一步研究了幾何光學和經典力學的對應性,幾何光學中的費馬原理和經典力學中的莫培丟變分原似,他大膽設想,不僅光具有粒子性和波動性兩種性質,而且一般的物質也具有這兩種性質。德布羅意認為:既然粒子概念在波的領域里成功的解釋了令人困惑的光電效應,那么,波動概念也應該能解釋在粒子領域中令人困惑的定態問題。
1923年~1924年期間,德布羅意陸續發表了《波和粒子》、《光量子,衍射和干涉》等論文,提出了物質波的概念,他認為一個能量為E ,動量為P 的粒子與頻率為γ,波長為λ的波相對應。仿照愛因斯坦關系,粒子的能量、動量與相應的頻率、波長之間的關系為:
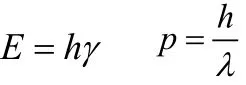
這個關系我們稱之為德布羅意關系。
在此基礎上,他用物質波概念分析了玻爾量子化條件的物理基礎。氫原子中電子波繞原子核的圓周軌道傳播一周后應光滑的連接在一起,否則將會由于干涉相互抵消,不能形成穩定軌道。這就要求軌道的周長應是波長的整數倍,即滿足:

式中r是電子繞核的軌道半徑,λ是電子波的波長。利用德布羅意關系,可以得出玻爾量子化條件:
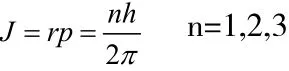
德布羅意的物質波假設在當時并沒有引起很大的注意,原因為:
首先,這個假設只是對玻爾的量子化條件提供了一個解釋方案,并沒有得出新的結論。其次,這種物質波究竟是什么東西,并不明確,在試驗上也沒有證實。最后,由于經典物理學的傳統概念,對粒子看作既是粒子又是波的觀念太超乎一般人的認識。
后來,德布羅意的導師朗之萬將他的論文推薦給愛因斯坦并得到了愛因斯坦的高度贊揚,這才引起人們的重視。薛定諤正是在愛因斯坦的建議下,對德布羅意的假說進行了仔細的研究,導致了波動力學的誕生。
1927年美國物理學家戴維遜和革莫用電子的衍射實驗證實了電子波的存在,而且也證實了德布羅意關系,德布羅意物質波的假設得到了實驗的證實。
2 玻恩對波函數的統計解釋
按照德布羅意物質波假設,一個能量為E ,動量為P 的粒子與頻率為,波長為λ的波相對應,在三維空間中,可以用樣一個平面波來代表它。C是常數,ψ(r, t)稱為波函數,那波函數又有什么物理意義呢。
起初,一些物理學家仍按照經典物理中的粒子和波相對立的觀點,總想將一個寓于另一個之中,或認為粒子性比波動性更基本,或認為波動性比粒子性更重要,但這些解釋都不能符合眾多的實驗事實。1927年,德國理論物理學家玻恩給出了波函數的統計解釋:波函數在空間某一點的強度即振幅絕對值的平方和在該點發現粒子的幾率成正比。
在證明電子具有波動性的衍射實驗中,當電子通過晶體衍射打到屏上時,出現明暗相間的衍射圓環,衍射環的明暗程度代表了到達那里的德布羅意波ψ的強度的大小。最亮的地方表示最大,最黑的地方表示=0。
當減小電子流的強度,以致電子可以一個一個的到達屏上時,在屏上出現的圖樣則變成完全是毫無規則的,只有當時間足夠長以后,有眾多的電子到達屏上之后,屏上才出現明暗相間的衍射條紋。這說明所描述的粒子遵循著滿足統計規律的運動。玻恩正是利用電子衍射實驗中出現的這樣特殊的規律,提出了他對波函數的統計解釋:波函數在空間某一點的強度(振幅絕對值的平方)和在該點發現粒子的幾率成正比。按照這個解釋,物質波又可以叫做幾率波。
按照波函數的統計解釋,波函數告訴了我們粒子在某處出現的幾率是多少,在另一處出現的幾率又是多少等等。當然這也是對粒子運動狀態的一種描述,因此量子力學中,對一個系統狀態的描述與經典力學中完全不同。在經典力學中,一個質點的運動狀態可以用它的位置和動量來確定,運動狀態隨時間的變化規律可以由牛頓定律來決定,即經典力學對質點的運動狀態給出了決定性的預言。但是在量子力學中,由波函數的統計解釋可知,對粒子運動狀態的描述是幾率性的,它不能告訴我們粒子到底在什么位置,只能告訴我們粒子處于某處的幾率大小。當系統由一種狀態變化為另一種狀態時,我們得到的仍然是系統狀態的幾率性描述。因此,量子力學中對粒子運動的描述沒有確定的軌道概念,我們對粒子運動狀態的演化只能給出幾率性預言,而不是決定性預言。造成這種現象的根本原因就是波粒二象性。
但是,量子力學中的幾率波和經典波是完全不同的。首先,經典波,例如聲波、水波等代表了某種介質中振動的傳播過程,而幾率波不代表任何介質振動,其次,經典波的振幅本身大小有絕對意義,它的平方和振動能量成正比,而幾率波振幅絕對值的平方表示該點發現粒子的幾率,同時由于波函數可以歸一化,所以幾率波的振幅卻可以任意乘以一個常數,但它們代表得卻是相同的物理狀態。
[1]屠慶銘.大學物理[M].北京:高等教育出版社,2009.
[2]陳信義.大學物理[M].北京:清華大學出版社,2008.
[3]宋峰.大學物理學基礎教程(下)[M].北京:高等教育出版社,2008.

