大間隙磁力傳動系統能量傳遞效率

劉云龍，譚建平，許焰,，劉志堅，祝忠彥（. 中南大學 機電工程學院，湖南 長沙，40083；. 長沙大學 機電工程系，湖南 長沙，40003）

大間隙磁力傳動系統能量傳遞效率

劉云龍1，譚建平1，許焰1,2，劉志堅1，祝忠彥1（1. 中南大學 機電工程學院，湖南 長沙，410083；2. 長沙大學 機電工程系，湖南 長沙，410003）

為了解大間隙、高轉速條件下磁力傳動系統的能量傳遞規律，研究行波磁場驅動的大間隙磁力驅動技術；通過微型軸流式血泵外磁場驅動，對大間隙磁力驅動系統各部分能量耗散進行研究，建立系統能量傳遞效率的數學模型。通過軸流式血泵泵水實驗，得到血泵在耦合距離20 mm和30 mm時的最大能量傳遞效率，即磁力傳動系統的最佳工作點，并通過與理論解析值相比較，得到大間隙磁力驅動系統的能量傳遞效率的變化趨勢，確定磁力驅動系統能量傳遞效率的主要影響因素，為提高磁力驅動系統的能量傳遞效率提供了途徑和依據。

大間隙；磁力傳動；軸流式血泵；能量傳遞效率；數學模型

非接觸磁力傳動方式是由Ikuta等[1]提出的，以現代磁學的基本理論磁性物質同性相斥、異性相吸的原理替代機械式傳動實現傳動為目的，應用永磁材料或電磁機構所產生的磁力作用，實現力或力矩非接觸式傳遞的一種新技術，已成為機械傳動研究領域的熱點[2?3]。Frana等[4]采用旋轉磁場方式來實現方形容器內部流體驅動，建立了系統磁力的計算模型。趙韓等[5]以向心電磁軸承為例，分析了渦流損耗與轉子轉速、勵磁電流頻率的關系；高殿榮等[6]提出運用永磁同步電機的原理，依靠線圈組的交變電流產生交變磁場來驅動永磁體轉動；Kilani等[7]提出通過利用永磁體產生的磁場作為外磁場來驅動微機械沿直線運動；張清等[8?9]應用解析法和有限元法對圓盤式磁力驅動器的渦流損耗進行了分析，對控制渦流損耗、提高傳動效率都具有指導意義。目前，在磁力傳動技術的研究及應用中，系統的主從磁極間隙均屬于小間隙范疇（小于3 mm[10?11]），而在特定的條件下，實際或期望的磁極間隙遠大于經典磁力傳動所設定的范圍。譚建平等[12?14]以軸流式血泵的外磁場驅動為背景，通過對磁力耦合、磁能傳遞機理的研究，提出了一種非觸式大間隙磁力驅動方法[12]，并建立了其空間磁場、空間磁力矩數學模型[15]，但空間磁力矩隨耦合距離的增大迅速衰減依然是磁力傳動技術的一大難題，本文作者針對大間隙磁力驅動系統，通過對系統各部分能量耗散進行研究，建立系統能量傳遞效率數學模型，以便為提高磁力傳動效率提供途徑和依據。

1 大間隙磁力傳動系統

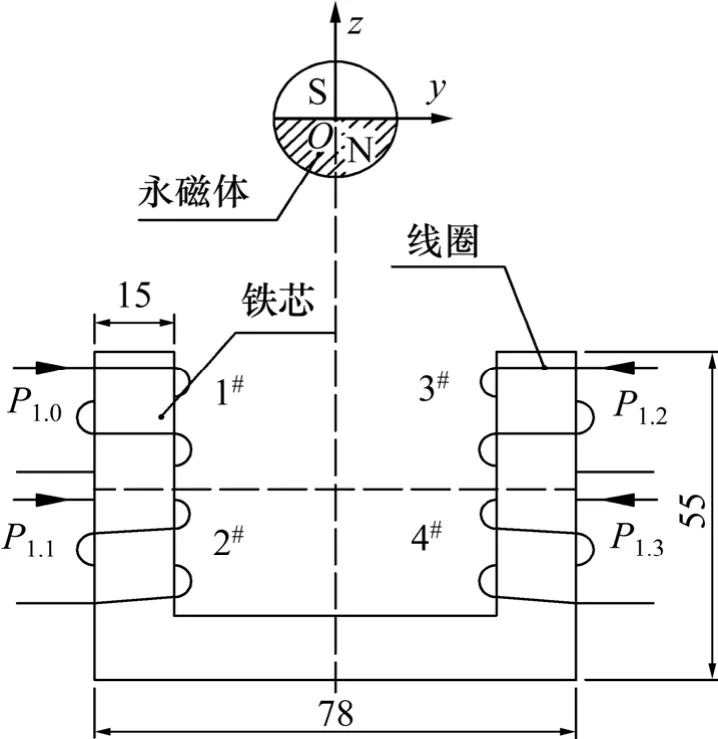
圖1 磁力驅動系統示意圖Fig.1 Schematic diagram of magnetic drive system

圖2 軸流式血泵示意圖Fig.2 Schematic diagram of axial-flow blood pump

圖3 大間隙磁力驅動系統能量傳遞框圖Fig.3 Block diagram of energy transfer in magnetic drive system

大間隙磁力驅動系統原理示意圖如圖1所示；軸流式血泵示意圖如圖2所示，由軸承、葉輪和永磁體等構成。圖3所示為系統的能量傳遞框圖，電能從直流電源輸出到電磁體，通過電磁體線圈上電壓（電流）時序的改變，實現其左、右磁場狀態的切換，產生行波磁場，將磁力矩傳遞給從動磁極（永磁轉子），從而帶動血泵葉輪等裝置旋轉工作，實現能量傳遞。文獻[13]詳細介紹了空間磁場的耦合機理和行波磁場的產生方法。

2 系統各部分能量損耗

2.1 渦流損耗

以單片硅鋼片為模型，建立如圖4所示坐標系OXYZ，硅鋼片的長、寬、高分別為a，b和d，設近似等效后的正弦交變磁場的方向平行于硅鋼片平面，在沒有自由電荷、傳導電流的線性各向同性介質中，麥克斯韋方程組的微分形式為：

式中：E為電場強度；H為磁場強度；σ為電導率；μ為磁導率。

圖4 硅鋼片電磁場分析模型坐標圖Fig.4 Magnetic field analytical model coordinate graph of single chip silicon steel sheet

由此可得單位體積硅鋼片內的渦流損耗功率為：

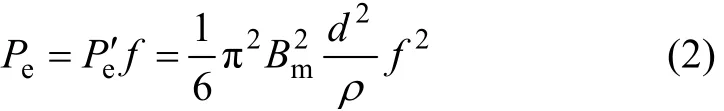
式中：Bm為電磁體磁感應強度幅值；ρ為硅鋼片電阻率；f為電磁體磁場脈沖頻率。

2.2 磁滯損耗

磁滯損耗來自磁化過程。在磁化過程中的磁滯回線面積表征了這個過程中磁滯損耗。磁化1周的磁滯損耗能量為：

在對電磁體單邊的鐵心交替磁化的過程中，由于B和H之間并不呈線性關系，使得磁滯損耗的計算變得比較困難。在瑞利區域內，磁滯回線（如圖5所示）可以用下面的公式表示：

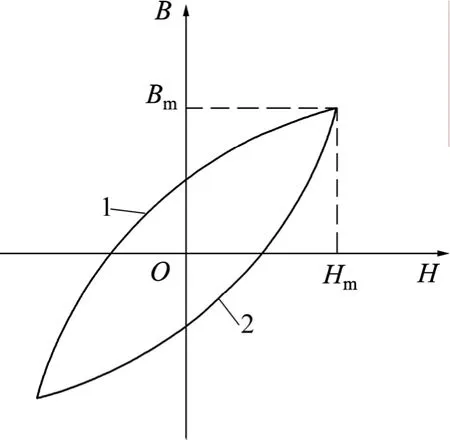
圖5 瑞利區域的磁滯回線Fig.5 Hysteresis loop of Rayleigh area

式中：“+”號代表回線的上支（圖5中曲線1）；“-”號代表回線的下支（圖5中曲線2）。則磁化1周的能量損耗為：

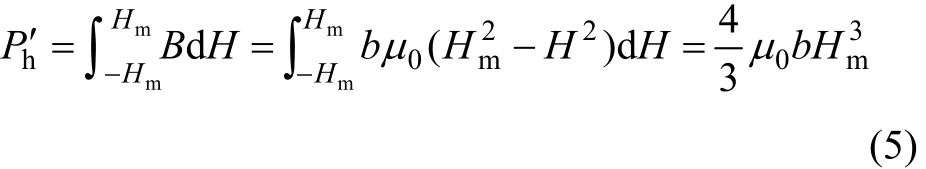
由此得到電磁體鐵芯的磁滯損耗功率為：

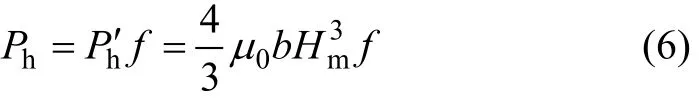
2.3 銅損

當電磁體線圈通電時，由于銅絲本身的電阻以及線圈在交變電流作用下產生的感抗，均會以熱能形式消耗功率，這部分損耗功率稱為銅損。由線圈的磁場強度計算公式為H=NI/l，得到線圈的自感系數為：

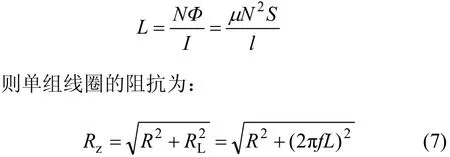
當電路接通時，有且僅有2組線圈同時導通，因此，可得電磁體線圈銅絲發熱損耗功率為：

式中：I為通過單相繞組的電流；R為單組線圈電阻；f為通入的交變電流頻率；N為單組線圈匝數；S為線圈橫截面積；l為線圈長度。

3 能量傳遞效率數學模型

設直流電源輸出電壓為U，輸出電流為I，則直流電源輸出功率為：

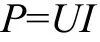
電磁體的輸出功率為：

式中：P為電源輸入功率（即電磁體輸入功率）；P1為電磁體輸出功率；P2為電磁體損耗。

根據已經建立的大間隙磁力傳動系統驅動力矩計算模型式[15]：

式中：θ為永磁體的轉角；l為永磁體軸向長度；r1和r2分別為永磁體內、外徑；M為永磁體磁化強度；By和Bz分別為電磁體空間磁場y方向和z方向的分量。若ω為血泵轉子角速度，則軸流式血泵永磁轉子的輸出功率為：

由式（9）和（11）得到系統大間隙能量傳遞效率的數學模型：

4 實驗

4.1 實驗系統模型

以軸流式血泵驅動為研究對象，建立大間隙磁力驅動血泵泵水實驗系統，如圖6所示。根據流體力學相關理論，可得實際泵水消耗功率（以Ps表示）和回路損耗功率（以Ph表示）分別為：

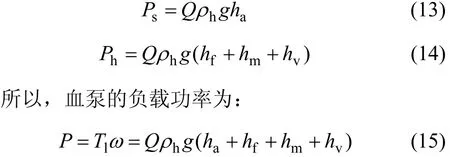
式中：Tl為血泵負載扭矩；ω為血泵轉子角速度；Q為回路流量；hρ為水溶液密度；ha為凈揚程（即泵水回路揚程）；hf為管路沿程損失；hm為管接頭局部損失；hv為血泵出口能量轉化的水柱高度。

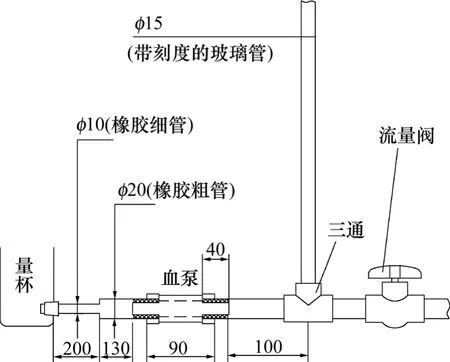
圖6 軸流式血泵泵水實驗系統Fig.6 Experimental system of axial-flow blood pump

由此得到大間隙磁力驅動系統能量傳遞效率的實驗模型：

4.2 實驗條件及步驟

4.2.1 實驗條件

電磁體參數如下：電磁體鐵芯采用厚度為0.35 mm的硅鋼片疊成（硅鋼片尺寸如圖2所示，由71片疊成），線圈匝數為650匝，線徑為0.31 mm；軸流式血泵參數如下：永磁轉子內半徑r1=1 mm，外半徑r1=6 mm，軸向長度l=15 mm，磁化強度M=900 kA/m；實驗參數如下：電磁體與血泵永磁轉子耦合距離分別為20 mm和30 mm，泵水實驗回路尺寸參數如圖6所示。4.2.2 實驗步驟

（1） 調節電磁體與血泵永磁轉子耦合距離為20 mm；設定直流電源為恒流輸出狀態，電流初值為I=0.5 A，按下啟動按鈕，使血泵逐漸加速至轉速n=3 000 r/min，調節電流旋鈕，改變輸出電流，找到系統長時間維持3 000 r/min轉速所需最小電流，記錄當前電源輸出參數（電壓U和電流I）；此時，對應的玻璃管（如圖6所示）中的水柱揚程為系統零流量下的凈揚程，然后，將流量閥門開啟一個角度。隨著開啟角度的增大，玻璃管中水柱高度下降的幅度也隨之增大，待水柱高度穩定后，記錄當前水柱凈揚程；啟動秒表，同時將閥門另一端流出的水接入量具，大約2 min，停止計時，同時關閉閥門。由以上實驗得到一組實驗參數：I，U，Q，ha和n。

通過以上步驟，即得到轉速為3 000 r/min時的流量Q、凈揚程ha，以及最小輸入功率P=UI。重復以上步驟，分別得到耦合距離20 mm時，血泵在3 000～9 400 r/min時的各實驗參數。

（2） 調節電磁體與血泵永磁轉子耦合距離為30 mm；重復步驟（1），即得到耦合距離30 mm時，血泵在各轉速下的實驗參數。

4.3 實驗結果

通過實驗步驟（1）和步驟（2），分別得到電磁體與血泵永磁轉子在耦合距離分別為20 mm和30 mm時的實驗參數，分別如表1和表2所示。

由式（11）可知：軸流式血泵永磁轉子的輸出功率為P=ωT，由文獻[15] 建立得系統驅動力矩計算模型式可知：驅動力矩同電流成正比。將電磁體參數和實驗參數代入式（10），得到不同耦合距離下，1個耦合周期內的平均磁力矩T與電流的關系曲線。

由式（15）可知：軸流式血泵的負載功率為P=Tlω。由表1和表2的實驗參數，得到各個電流下的負載扭矩Tl與電流的關系曲線。耦合距離為20 mm和30 mm時，驅動扭矩T與負載扭矩Tl的對比曲線分別如圖7和圖8所示。

表1 耦合距離為20 mm時實驗參數Table 1 Experimental data under coupling distance of 20 mm

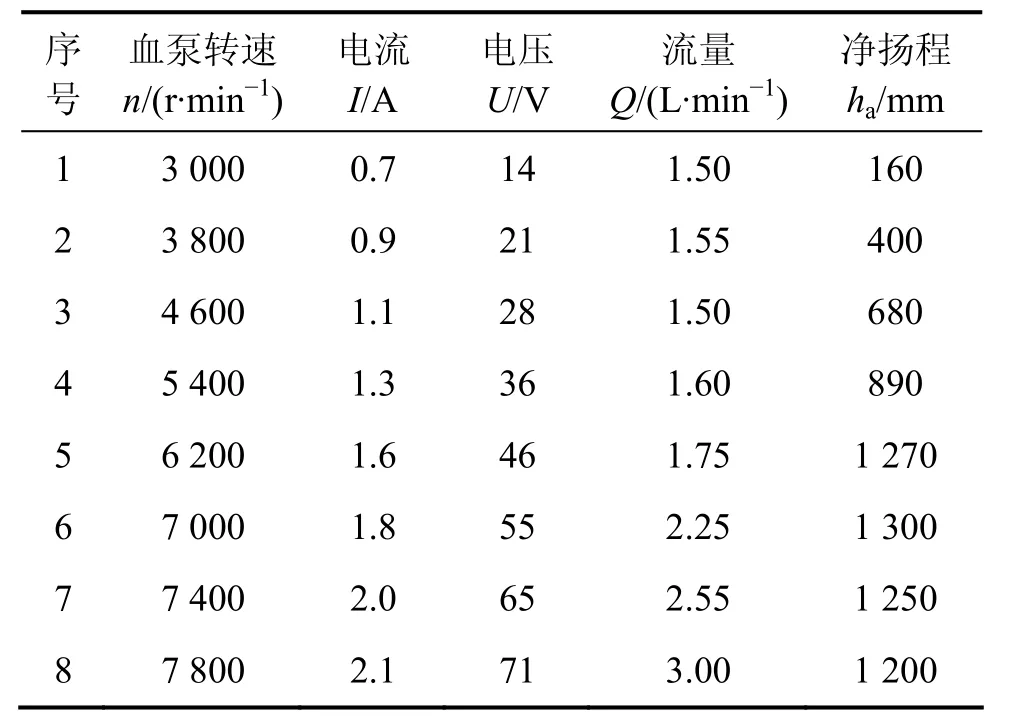
表2 耦合距離為30 mm時實驗參數Table 2 Experimental data under coupling distance of 30 mm

圖7 耦合距離20 mm時T與Tl對比曲線Fig.7 Comparison of T and Tl under coupling distance of 20 mm

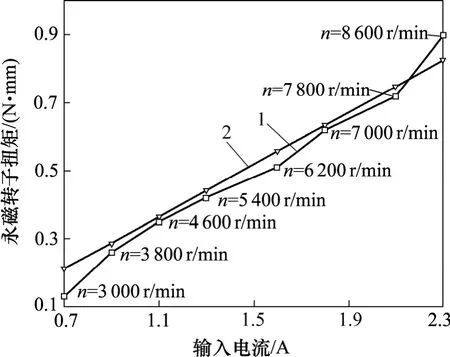
圖8 耦合距離30 mm時T與Tl對比曲線Fig.8 Comparison of T and Tl under coupling distance of 30 mm

圖7和圖8中，各負載扭矩Tl上所標示的轉速，均對應耦合距離處相應電流下的最大驅動能力。

將T，Tl以及表1、表2中各實驗參數分別代入能量傳遞效率數學計算模型式（12）和實驗模型式（16），得到系統在耦合距離為20 mm時能量傳遞效率的理論值、實驗值，以及耦合距離為30 mm時的能量傳遞效率的實驗值，如圖9所示。

圖9 不同耦合距離下的能量傳遞效率對比曲線Fig.9 Comparison of efficiencies under different coupling distances

4.4 分析

（1） 圖7和圖8所示為驅動扭矩T與負載扭矩Tl在不同耦合距離下的對比曲線。可見：驅動扭矩取決于輸出電流，并且與電流成正比關系，而負載扭矩取決于血泵轉速；血泵的驅動扭矩T與負載扭矩Tl之間的差值來源于血泵本身的機械損耗。

（2） 耦合距離20 mm時，驅動扭矩大于負載扭矩，轉速為9 000 r/min時兩者最為接近；隨著電流的進一步增大，系統能輸出更大的驅動能力；當耦合距離30 mm時，驅動扭矩同負載扭矩在2.1 A以及7 800 r/min處交匯，之后負載扭矩大于驅動扭矩，理論上不能驅動。實驗證明：當電流達到2.1 A，血泵轉速達到7 800 r/min時，系統能量傳遞效率已經明顯開始下降，在增大電流至2.3 A后，仍沒有達到下一個速度等級（8 200 r/min）的驅動能力。

（3） 圖9所示為能量傳遞效率對比曲線。由耦合距離20 mm時能量傳遞效率實驗值和理論值的比較，可以看出：隨著輸入電磁體脈沖頻率的增大，血泵轉速的增加，系統能量傳遞效率逐漸提高，但并不是無限提高；由理論解析求得，在一定電磁參數條件下，系統在轉速為9 000 r/min時，能量傳遞效率達到了最大值，經過對9 000 r/min附近各轉速進行試驗，得到了與理論計算結果相同的實驗結論，驗證了理論模型的正確性。

（4） 當耦合距離分別為20 mm和30 mm時，從能量傳遞效率實驗值的對比中可以看出：當耦合距離為30 mm時，系統在7 000 r/min達到額定工作點，遠低于耦合距離20 mm時的額定工作點；當耦合距離為30 mm時的最大效率僅為2.9%，遠遠小于耦合距離為20 mm時的8.0%。隨著耦合距離的增大，系統驅動力矩呈平方次衰減，所以，系統能量傳遞效率隨著耦合距離的增大而急速降低。

（5） 從能量傳遞效率模型式（12）和式（16）可以看出：影響能量傳遞效率的因素較多，但總的來說，主要來自于3個方面：電磁體、血泵以及泵水回路。在保證驅動扭矩（即保證血泵轉速）的前提下：采用更薄、具有更大磁導率的材料制作鐵芯，增大電磁體磁能輸出；采用具有更大磁能積的材料制作血泵永磁轉子；盡可能減小輸入電流，從而減小渦流損耗、磁滯損耗以及銅損，進而提高效率。

5 結論

（1） 針對提出的非接觸式大間隙磁力驅動方法，通過對磁力驅動系統各部分能量耗散的研究，建立了系統能量傳遞效率的數學模型和實驗模型。

（2） 通過軸流式血泵泵水實驗，得出了驅動扭矩與負載扭矩在不同耦合距離時的對比曲線，以及血泵在耦合距離20 mm和30 mm時的最大能量傳遞效率分別為8.0%和2.9%。

（3） 通過將實驗值與解析值進行對比分析，得出了系統能量傳遞效率的變化趨勢，驗證了模型的正確性，分析了實驗值與解析值之間偏差的產生原因。

（4） 通過對磁力驅動系統能量耗散模型的研究，從能量和效率的角度，提出了磁力驅動系統的優化方案，為提高磁力驅動系統的能量傳遞效率提供了途徑和參考。

[1] Ikuta K, Makita S, Arimoto S. Non-contact magnetic gear for micro-transmission mechanism[C]//Proceedings of the 1991 IEEE Micro Electro Mechanical Systems. New York： IEEE, 1991： 125?130.

[2] 徐先懂, 龔中良, 譚建平. 基于外磁場耦合的血泵驅動系統[J]. 中南大學學報： 自然科學版, 2007, 38（4）： 711?714.

XU Xian-dong, GONG Zhong-liang, TAN Jian-ping. Blood pump driven system based on extracorporeal magnetic filed couple[J]. Journal of Central South University： Science and Technology, 2007, 38（4）： 711?714.

[3] 趙韓, 王勇, 田杰. 磁力機械研究綜述[J]. 機械工程學報, 2003, 39（12）： 31?36. ZHAO Han, WANG Yong, TIAN Jie. Review of study on magnet machine and mechanism[J]. Chinese Journal of Mechanical Engineering, 2003, 39（12）： 31?36.

[4] Frana K, Stiller J. A numerical study of flows driven by a rotating magnetic field in a square container[J]. European Journal of Mechanics B/Fluids, 2008, 27（4）： 491?500.

[5] 趙韓, 李露, 王勇. 電磁軸承中磁場時間和空間變化對渦流的影響[J]. 農業機械學報, 2007, 38（6）： 129?133.

ZHAO Han, LI Lu, WANG Yong. Influence of changing the magnetic field on eddy current effect of electromagnetic bearing[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38（6）： 129?133.

[6] 高殿榮, 韓康壯. 血泵轉子遠場驅動的原理及分析[J]. 液壓氣動與密封, 2008, 28（4）： 39?42.

GAO Dian-rong, HAN Kang-zhuang. Principle and research on far field driving system of blood pump[J]. Hydraulics Pneumatics and Seals, 2008, 28（4）： 39?42.

[7] Kilani M I, Jaw S Y, Haik Y, et al. Numerical simulation of flow in a screw-type blood pump[J]. Journal of Visualization, 2005, 8（1）： 33?40.

[8] 張清. 圓盤式磁力驅動器的渦流分析[D]. 吉林： 吉林大學機械科學與工程學院, 2008： 43?62.

ZHANG Qing. Study on eddy current in discal magnetic driver[D]. Jilin： Jilin University. School of Mechanical Science and Engineering, 2008： 43?62.

[9] 鄭福勝, 譚慶昌, 張清, 等. 盤式磁力驅動器隔離套的渦流損耗分析[J]. 工程與試驗, 2008（3）： 62?66.

ZHENG Fu-sheng, TAN Qing-chang, ZHANG Qing, et al. Study on eddy current in partition of discal magnetic drivers[J]. Engineering and Test, 2008（3）： 62?66.

[10] 倪平濤, 王開文, 陳健. 一系縱向定位間隙對磁流變耦合輪對車輛橫向動力學性能的影響[J]. 交通運輸工程學報, 2007, 7（2）： 6?9.

NI Ping-tao, WANG Kai-wen, CHEN Jian. Influence of primary longitudinal position clearance on lateral dynamics of vehicle with MRF coupled wheelsets[J]. Journal of Traffic and Transportation Engineering, 2007, 7（2）： 6?9.

[11] 興濤, 楊建波, 郭永獻. U型磁鐵磁路分布與氣隙磁感應強度[J]. 機械設計與制造, 2008（7）： 82?83.

XING Tao, YANG Jian-bo, GUO Yong-xian. Hypotheses of a U type magnet circuit distributing and the calculating and testifying on the air gap intensity of magnetic induction[J]. Machinery Design and Manufacture, 2008（7）： 82?83.

[12] 譚建平, 許焰, 劉云龍, 等. 一種非接觸式大間隙磁力驅動方法： 中國, 200810030545.1[P]. 2008?10?01.

TAN Jian-pin, XU Yan, LIU Yun-long, et al. A non-contact large floating interval magnetic force driving method： China, 200810030545.1[P]. 2008?10?01.

[13] 龔中良, 譚建平. 外場驅動血泵磁力耦合傳動受力分析[J].機械科學與技術, 2006, 25（6）： 725?727.

GONG Zhong-liang, TAN Jian-ping. Analysis of the magnetic coupling force transmission in extra magnetic field driven blood pumps[J]. Mechanical Science and Technology, 2006, 25（6）： 725?727.

[14] 徐先懂, 譚建平. 基于磁能傳遞的血泵驅動系統研究[J]. 機械, 2006, 33（10）： 7?9.

XU Xian-dong, TAN Jian-ping. Research of blood pump driven system based on magnetic energy transmission[J]. Machinery, 2006, 33（10）： 7?9.

[15] 許焰, 譚建平, 劉云龍, 等. 大間隙磁力傳動系統驅動力矩的計算方法[J]. 湖南大學學報： 自然科學版, 2009, 36（7）： 30?35.

XU Yan, TAN Jian-ping, LIU Yun-long, et al. Calculation method of driving torque of the large gap magnetic drives system[J]. Journal of Hunan University： Science and Technology, 2009, 36（7）： 30?35.

（編輯 楊幼平）

Energy transfer efficiency of large gap magnetic drive system

LIU Yun-long1, TAN Jian-ping1, XU Yan1,2, LIU Zhi-jian1, ZHU Zhong-yan1

（1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China; 2. Department of Mechanical and Electrical Engineering, Changsha University, Changsha 410003, China）

In order to research the energy transfer law in large gap magnetic drive system under the condition of large gap and high speed, the large gap magnetic drive technology, which was driven by traveling wave magnetic field, was studied. Based on the outside magnetic driving system of axial flow blood pump, the mathematical model of energy loss was established through studying each part of the system. By the driving experiment of blood pump, the maximum energy transfer efficiencies at 20 mm and 30 mm are obtained, which is the optimal operating condition of system. Then change tendency of the energy transfer efficiency and its influential factors are obtained by analysis and experiments, so as to provide methods improving the energy transfer efficiency.

large gap; magnetic drive; axial flow blood pump; energy transfer efficiency; mathematical model

TH139

A

1672?7207（2011）05?1296?07

2010?03?30；

2010?07?28

國家高技術研究發展計劃（“863”計劃）項目（2006AA02Z4E8）；國家自然科學基金資助項目（50775223，50875266）；教育部博士學科點專項基金資助項目（20070533125）；湖南省教育廳科研資助項目（08C138）；湖南省研究生科研創新項目（CX2010B072）

譚建平（1963?），男，湖南攸縣人，教授，博士生導師，從事現代機電液控制理論與技術研究；電話：13607311991；E-mail： jptan@163.com