非對稱信息下鐵路重載集疏運一體化利益分配博弈

馮芬玲，藍丹

（中南大學 交通運輸工程學院，湖南 長沙，410075）

非對稱信息下鐵路重載集疏運一體化利益分配博弈

馮芬玲，藍丹

（中南大學 交通運輸工程學院，湖南 長沙，410075）

分析非對稱信息下集疏運利益分配的原則及要素，在此基礎上建立利益分配模型，采用多階段博弈進行求解。采用Shapley值法的最小距離解對模型求解過程進行修正。研究結果表明：在集疏運中，創新所承擔的風險越大，利益分配比例越低；工作貢獻系數越大，利益分配比例越高；基于協商讓利的原則，使得風險相對均攤，保護小企業和有潛力的合作企業；模型能較好地解決非對稱信息下集疏運的利益分配問題，驗證了模型的合理性和適用性。

鐵路；重載運輸；集疏運一體化；利益分配；博弈分析

“集疏運一體化”是將集、疏、運三過程視為不可分割的整體，統一技術作業過程，統一編制集、疏、運計劃，統一組織實施新的鐵路貨運組織模式。在鐵路重載運輸集疏運中，港口、運輸企業相互協同運作，形成網鏈結構，它們之間既有競爭，也有合作。重載運輸集疏運整體收益是全體成員共同努力創造的，因而在進行收益分配決策時，不僅僅要考慮追求自身收益的最大化，同時還要考慮到自身的收益分配與其他企業的收益分配相互間的影響，以此維護整個集疏運體系的穩定以及促使整體收益優化。也就是說，各成員在收益分配選擇時要受到其他企業選擇的影響，同時，反過來也影響到其他企業，最終需要尋找到一種收益分配的均衡。利益分配直接關系到集疏運體系的運營效率、整體利益和整個體系中各成員的切身利益，這對于提高集疏運的運營組織效率和成員企業的積極性至關重要。目前，國內外對利益分配的研究較多，但大多是關于供應鏈和虛擬企業戰略聯盟的利益分配，如利用夏普利（Shapley）值法進行求解[1?9]、結合博弈論有關理論進行利益分配[10?20]、利用模糊數學等理論進行利益分配[21?24]等。然而，對于鐵路重載運輸集疏運一體化這種新的模式，目前還沒有具體的利益分配研究。為此，本文作者考慮到集疏運一體化的網鏈結構、企業的直接相互作用決策以及決策的均衡問題，建立非對稱信息下集疏運一體化的利益分配博弈模型，并對其進行算例分析。

1 利益分配原則與要素

1.1 利益分配原則

鐵路重載運輸集疏運一體化利益分配是指按一定的依據和原則在參與集疏運的企業之間分割一定時期內的合作利益的過程。為了盡量使集疏運中每個企業所獲得的分配與其期望的利益相一致，在利益分配時必須樹立公正、公平、有效、合理的分配原則。平等原則是利益分配最基本的原則，公平兼顧效率、協商讓利、民主決策、多勞多得是促進集疏運合理進行利益分配的原則。此外，還有以下幾個很重要的原則，保證集疏運利益分配公平公正的進行。

（1） 投入與利益對稱原則。整個集疏運企業在制定利益分配方案時，應充分考慮各企業i參與集疏運所投入的資源價值及其消耗程度。在其他條件相同的情況下，若企業i和j投入到集疏運的資源的復合指數Wi＞Wj，則它們從集疏運分配中所獲得的利益ui＞uj，即：

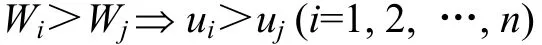
式中：Wi和Wj分別為企業i和j投入集疏運的資源的復合指數，它與所投入資源的價值和消耗程度有關。

（2） 風險與利益對稱原則。在其他情況相同的條件下，若企業i和j在集疏運運作中所承擔的風險Ri＞Rj，則它們從集疏運分配中所獲得的利益ui＞uj，即：

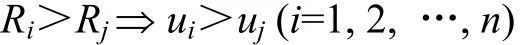
式中：Ri和Rj分別為企業i和j在集疏運運作中所承擔的風險系數。

若不考慮供應鏈企業成員獲得的收益與承擔的風險之間的關系，則成員企業就不會有積極性來承擔有風險的任務。

（3） 超加性原則。合作體的最大利益大于各方單干時所得的最大利益之和，否則沒有合作的可能性，即滿足條件：

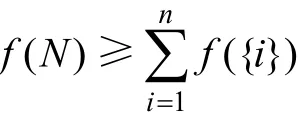
其中：f（N）為合作情況下合作體的最大利益為合作體各自單干時所得的最大利益之和。

（4） 個體理性原則。合作企業從合作利益分配所得的利益要大于單干得到的利益，即滿足條件：

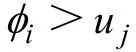
其中：φi為合作各方從合作利益中分配得到的利益；uj為合作各方獨自單干時得到的最大利益。

（5） 集體帕累托原則。合作企業從合作利益分配所得的利益之和等于合作體的最大利益，即滿足條件：，則說明合作的整體利益中存在有未被分配的利益，合作的個體將不會同意接受iφ的分配方案；若則說明這是違背超加原則的，合作的企業將不會愿意參加合作。

1.2 利益分配要素

由于集疏運體系中成員之間存在“私有信息”，造成信息的非對稱性，由此導致利益分配不對稱；因此，了解利益分配相關要素之間的關系是非常必要的。主要的利益分配要素如下。

（1） 成本要素分析。投入成本是成員企業參與利潤分配的基本要素。當每個成員企業都追求各自成本最低時，很可能會造成集疏運整體服務水平下降。通過成員企業間的合作競爭，所有集疏運成員能夠分享業務計劃，預測需求信息等信息。每個成員企業的直接生產成本（或服務成本）在一定的集疏運服務水平下達到最優，此時，企業付出的成本在集疏運體系提供的最終產品的成本中所占的比例，是企業獲取收益的參照標準。

（2） 貢獻度分析。在運輸企業中，運輸是產生價值的過程。在集疏運系統中，多個沒有行政隸屬關系或者股權強制控制關系的企業組成了合作型的運輸組織網絡，在該運輸組織網絡中，每個企業的貢獻量也是進行利益分配時必須考慮的要素之一。

（3） 企業在集疏運體系中所承擔的風險。這里的風險包括整個運輸體系目標達成的風險、市場風險以及合作風險、技術風險等等。

（4） 品牌與商譽。為了吸引客源，集疏運體系有時必須借助伙伴企業的品牌和商譽。

2 非對稱信息下鐵路重載運輸集疏運一體化收益博弈分配模型

2.1 基本假設

鐵路重載運輸集疏運一體化是各成員企業在平等互利的基礎上形成的合作體。在實際運營中，各成員企業的大部分合作行為主要依靠信息網絡、信任和契約機制來完成。各企業都具有很強的法人獨立性，它們出于自身利益的考慮，會使得其目標不完全一致，在選擇行動策略時總是以個體利益最大為目標；各企業由于時間、地域、文化等存在差異，其信息交流的時效性可能存在滯后的現象；各企業收集相關信息受到成本控制以及信息篩選能力的影響。這些都導致了各成員企業“隱藏”部分或全部重要信息，即使這種“隱藏”并非主觀意愿造成。所以，在整個集疏運體系中，必然存在信息不對稱問題。

為便于探討在非對稱信息下集疏運一體化的收益分配問題，需進行一些基本假設，對其進行簡化。

（1） 集疏運利益的分配是對整個集疏運過程中產生的總收益進行分配。設參與集疏運過程的企業成員個數為n，則有成員集N={1, 2, …,n}。

（2） 假設每個成員企業都有同等的無窮耐心，即利益分配的貼現率δ=1。

（3） 各成員企業均符合“理性人”假設，且均為風險中性。

（4） 設各成員企業i（1, 2, …,n）的努力水平為ai，具有不可觀測但可證實的特性，a=（a1,a2, …,an）為成員企業的努力水平向量。

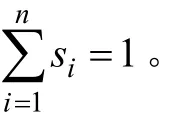
2.2 模型的建立與求解

由以上分析可知：企業通過相互作用來實現集疏運的目標，其中很大部分通過各成員的努力水平來表現，因而，假設集疏運總利益函數為E（f,a）。其中：a為成員企業的努力水平向量；f為其他影響因素的綜合因子。

集疏運的進行伴隨著創新性活動的開展，因此，各成員企業的成本由生產性成本和創新性成本2部分組成。其中：生產性成本是可以計算和度量且相對固定的，認為是一個與努力程度無關的常數；而創新性成本與努力程度相關，它隨努力程度的增加而增加，且增加的速度遞增。所以，成員企業i投入到集疏運運行中的總成本可表示為：

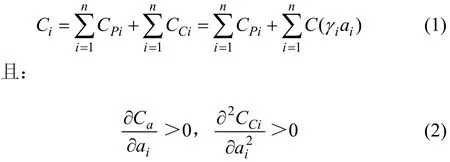
式中：Ci為成員企業i投入到集疏運運行中的總成本；CPi為成員企業i投入到集疏運運行中的生產性成本；CCi為成員企業i投入到集疏運運行中的創新性成本，因為其與努力水平向量a相關，故有（其中，γi為企業創新性活動成本系數）。

根據假設條件以及式（1）可以得到集疏運整體凈收益以及企業在集疏運中獲得的凈收益為：

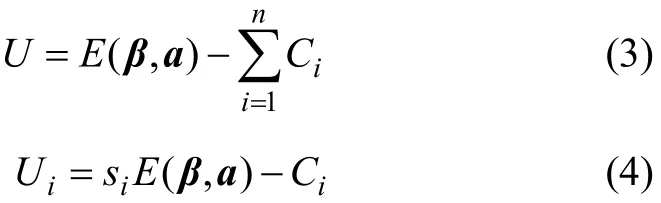
式中：U為集疏運一體化整體凈收益；Ui為成員企業i在集疏運一體化中所獲凈收益；β為工作貢獻系數向量，其取決于各成員企業投入到集疏運一體化中的能力對集疏運收益的作用。

對于式（3）和（4），假定U是a的嚴格遞增凹函數，即成員企業或港口工作越努力，凈收益越高，但努力的邊際產出率遞減，這也符合經濟學上的生產要素邊際報酬遞減法則，所以，有：

非對稱信息下集疏運的利益分配問題轉變為求解一定約束條件下的集疏運整體凈收益最大的問題，即有如下利益分配模型：模型中U由式（3）確定，Ui由式（4）確定。

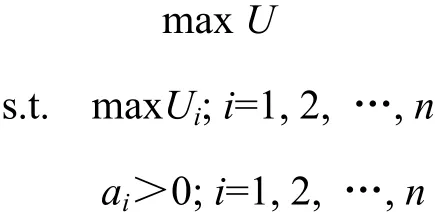
對該利益分配模型求解，實際上就是確定集疏運最合理的利益分配比例si以及集疏運各成員在協議的利益分配方案下納什均衡努力水平ai的過程。

為便于研究，假設有由鐵路企業A和2個公路企業（即B與C）組成的最簡單的集疏運一體化（從經濟學上來講，只有3個成員的非對稱信息下的集疏運簡單分配模型已包含其他復雜的多企業或港口集疏運的分配求解思路與基本結論），其中鐵路企業A為盟主，B和C為盟員，該集疏運滿足2.1節中的各基本假設。設ai（i=1, 2, 3）分別代表A，B和C的工作努力水平；βi（i=1, 2, 3）分別代表A，B和C的工作貢獻系數；γi（i=1, 2, 3）分別代表A，B和C的創新性活動成本系數；Ci（i=1, 2, 3）分別代表A，B和C的集疏運投入總成本；CPi（i=1, 2, 3）分別代表A，B和C的生產性成本；CCi（i=1, 2, 3）分別代表A，B和C的創新性成本；U（i=1, 2, 3）代表集疏運整體凈收益；Ui（i=1, 2, 3）分別代表A，B和C三成員企業在集疏運中所獲凈收益；s1，s2，s3分別代表A，B和C三成員企業在集疏運中的分配比例，且s1+s2+s3=1。為了研究問題方便，不失一般性，可以進一步假設三成員企業的創新性成本以及集疏運的總收益均為努力水平的二次函數，并且：

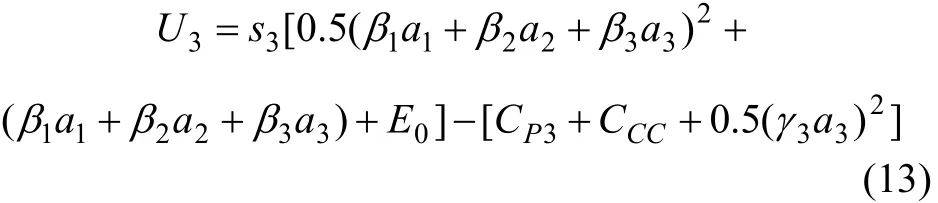
對式（10）～（13）進行兩步求解，即先確定納什均衡的努力水平，再確定分配比例。

2.2.1 納什均衡下努力水平的確定

假定利益分配比例已定，分析各成員企業怎樣選擇自己的行動（即努力水平）。根據式（11）～（13）分別對a1，a2和a3求偏導并令其等于0，求解求導后的方程組，即可求得a1，a2和a3。

由此可知：企業成員追求自身最大收益時所付出的工作努力水平與自身的分配系數成正比，與自身的貢獻系數成正比，與自身創新性活動成本系數的平方成反比。

2.2.2 分配比例的確定

將求得的a1，a2和a3代入式（10），將其對s1，s2和s3求偏導并令其等于0，即可求得s1，s2和s3。

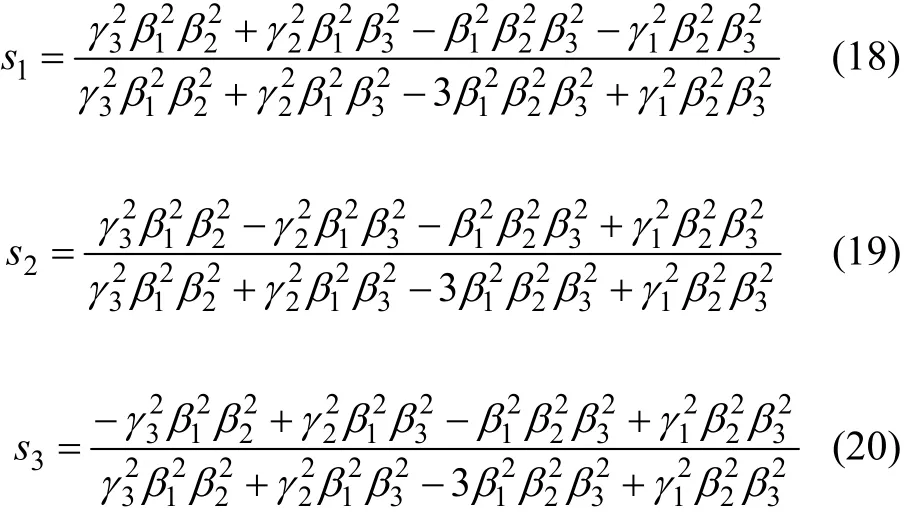
有時，s1，s2和s3不一定恒大于0，即存在某一合作成員在集疏運中沒有獲利的情況，也就是說，違背了投入與利益對稱原則和個體理性原則。因此，在進行利益分配之前，可以通過各成員企業的工作貢獻系數和創新性成本系數之間的關系來預算。

因此，式（21）為三方博弈下的利益分配比例均大于0的充要條件，即三方博弈下納什均衡成立的充要條件。三方的利益分配比例之比為：

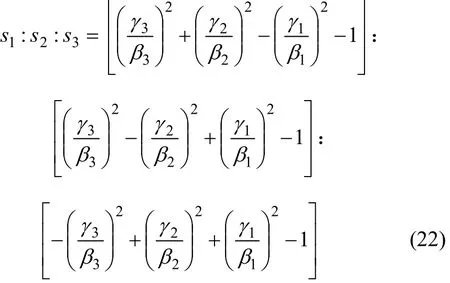
由式（22）可知：在另外2方的創新性成本系數和工作貢獻系數不變的情況下，降低自身的創新性成本系數和提高工作貢獻系數，其分配比例會增加。即降低自身的創新性成本系數，相應地會降低其在集疏運中所承擔的風險；再提高工作貢獻系數，其分配比例相應增加。這與實際情況是相符的。

當企業創新性成本系數較大時，在工作貢獻系數一定的情況下，該企業的分配比例會較小，而企業是以獲利為最終目標，因此，在這種情況下，成員企業會選擇降低創新性成本系數以此降低風險，增大其分配比例。這在一定程度上阻礙了集疏運的發展。此外，在實際利益分配過程中可能會出現不滿足式（21）的情況，即出現了理論上的分配比例小于0的情況。對于一個“理性個體”來說，這時它會選擇退出集疏運一體化組織，導致集疏運體系解散。但也有一些特殊情況使得該集疏運合作繼續進行下去，如分配比例小于0的企業是一個非常有潛力的企業，只是在現階段獲利比較少。面對這種情況，基于協商讓利原則、投入與利益對稱原則和個體理性原則，給出如下修正分配方案。

2.3 模型的修正

對于經濟或社會活動中若干實體相互合作從而獲得更多的經濟或社會價值這一類問題，稱為N人合作對策問題。鐵路重載運輸集疏運也屬于這一類問題。Shapley給出了解決該問題的一種方法[25]，稱Shapley值方法。Shapley值方法以嚴格的公理為基礎，在處理合作對策問題時具有公正、合理等特點。本文借助其求解利益分配的方法和思想，來修正本模型的求解過程。

根據Shapley值方法，將鐵路企業A、公路企業B和C記為I={1, 2, 3}。對于I的任意子集n對應著一個實值函數v（n）（v為對策的特征函數）。它表示I中參與集疏運的任意|n|方所對應的分配比例向量，沒有參與集疏運的企業其分配比例為0。此處考慮到集疏運需要鐵路和公路企業共同完成，不考慮單個企業完成運輸的情況。

首先求出兩方合作的特征函數v（1, 2），v（1, 3）和v（2, 3）。即求解鐵路A和公路B合作、鐵路A和公路C合作、公路B和公路C合作時的分配比例向量。用分別表示第1和第2方即鐵路企業A和公路企業B合作時鐵路A、公路B、公路C的利益分配比例。鐵路A和公路C、公路B和公路C合作時依此類推。求解方法與前述求解鐵路A和公路B與C合作時的分配比例的方法相同，可得：

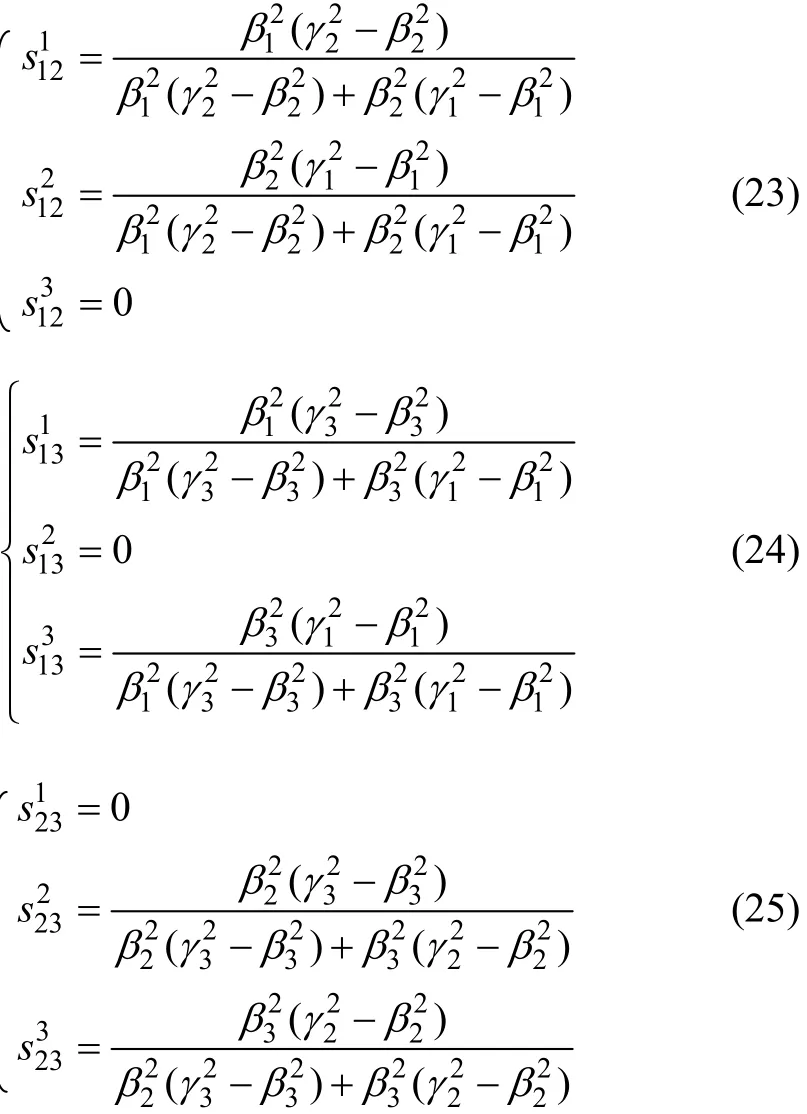
三方組成集疏運體系時的分配比例向量v（1, 2, 3）即為式（18），（19）和（20）所得結果。然后，綜合考慮v（1, 2），v（1, 3），v（2, 3）和v（1, 2, 3）的分配情況，在此基礎上構造出最小距離解。設存在一種三方均能接受的理想分配方案，記作S=（S1,S2,S3），其中，S1，S2和S3即為修正后A，B和C三企業的利益分配比例。追求這個分配結果與v（1, 2），v（1, 3），v（2, 3）和v（1, 2, 3）的分配結果的距離最小。記S12，S13，S23和S123分別表示鐵路企業A和公路企業B合作、鐵路企業A和公路企業C合作、公路企業B和公路企業C合作以及三企業合作的分配方案，利用向量的2-范數，有

解式（26）～（28）即可得成員企業的利益分配比例。由此可知：當某企業具有非常大的潛力，集疏運組織有與其合作的必要時，以及為了刺激企業創新，促進集疏運的發展，選擇該修正后的模型，能得到較滿意的分配方案。

2.4 模型參數的確定

非對稱信息下集疏運利益分配模型中有2類參數需要確定：一是企業的貢獻系數iβ，二是企業的創新性成本系數iγ。本文在假定努力水平是實際工作時間價值情況下，分別對2類參數進行分析。

2.4.1 工作貢獻系數iβ的確定

在相同的環境和工作努力水平下，各個成員對整個集疏運過程做出的貢獻不一樣，即工作貢獻存在差異。其主要原因在于各自的投入能力不一樣，可以通過貢獻系數來衡量。鐵路重載集疏運一體化是通過整合各成員企業的相關資源來實現貨物的位移。在貨物的位移過程中，每一個參與的運輸企業都必須投入一定的資源來保證集疏運一體化的實施，故貢獻系數可以用單位時間內參與的運輸企業所投入的資源價值的相關表達式來表示。集疏運中所涉及的投入資源包括資本、人力資源、技術、信息和管理5種，則各成員企業單位時間內投入的資源總價值計算如下：

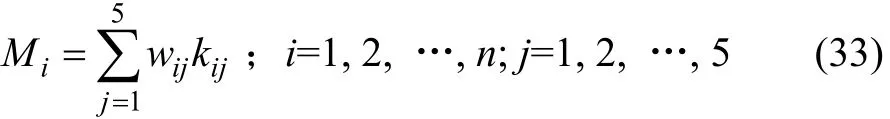
式中：Mi為單位時間內i企業投入的資源總價值；kij為單位時間內i企業投入的第j種資源價值，可以由相關專家或評估師進行資源價值評估獲得；wij為i企業投入的第j種資源的權重，可通過層次分析法獲得。則工作貢獻系數可由單位時間內各成員企業與同行業投入的資源總價值的平均值的比值來確定：

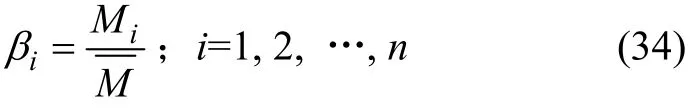
式中：為單位時間內同行業投入的資源總價值的平均值。

2.4.2 創新性成本系數iγ的確定

鐵路重載集疏運一體化在其發展過程中，需要不斷地創新，優化運輸組織模式，提高運輸速度與質量。在該過程中，高素質的人才是必不可少的。同時，在集疏運一體化過程中，準確及時的信息共享能提高貨物運輸效率，因此，開發信息技術也是創新的一部分。在尋求高素質人才過程中，主要有兩類人力資源成本：一是人力資源資本化的價值；二是人力資源的使用所創造出來的價值。開發信息技術需要開發、生產、維護信息的成本，包括設計成本、技術性成本、人力資源成本、設備費用、維護費用等。因此，創新性成本包括集疏運發展期間分攤的人力資源成本和信息成本，分為固定成本（如設備費用）和可變成本2部分。

由此創新性單位時間的可變成本計算公式為：

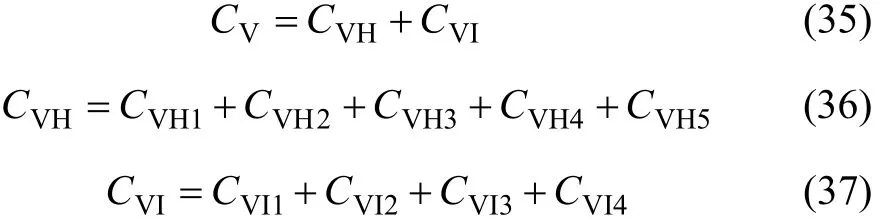
式中：CV為創新性單位時間可變成本；CVH為單位時間人力資源成本；CVH1為單位時間取得成本，即招聘成本、選拔成本、雇傭和安置成本；CVH2為單位時間開發成本，即定向成本、脫產培訓成本和在職培訓成本；CVH3為單位時間使用成本，即企業支付的、不包括獎金的工作報酬；CVH4為單位時間保障成本，即勞動事故保障成本、退休養老保障成本和失業保障成本等；CVH5為單位時間離職成本，即離職補償成本；CVI為單位時間信息可變成本；CVI1為單位時間信息設計成本，即設計尋求有效信息的成本；CVI2為單位時間信息技術性成本，即收集和加工處理信息發生的成本；CVI3為單位時間人力資源成本，主要指信息人力資源成本；CVI4為單位時間內的信息維護費用。由此可以確定創新性成本系數iγ為：式中：為單位時間內同行業投入的創新性成本的平均值。

表1 各企業投入資源價值Table 1 Value of businesses to invest resources 萬元

表2 各企業投入創新性成本Table 2 Costs of businesses to invest in innovation 萬元

3 算例分析

某集疏運一體化由鐵路企業A與2個獨立的公路企業B和C組成。該集疏運的實際運行符合2.1節中的假設條件，成員企業的創新性成本和該集疏運的總收益均為努力水平的二次函數且符合式（10）～（13）的基本形式。該年各成員企業投入的資源價值（即1 a內i企業投入的第j種資源價值）見表1，投入的創新性成本見表2。該年同行業投入的資源總價值的平均值和同行業投入的創新性成本的平均值分別是203萬元和102萬元。該年集疏運創造的總收益為6 000萬元。

將表1中的數據代入式（33）和（34）即可求得工作貢獻系數，將表2中的數據代入式（35）～（38）即可求得創新性成本系數。結果見表3。

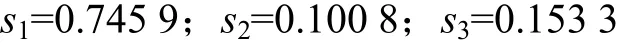
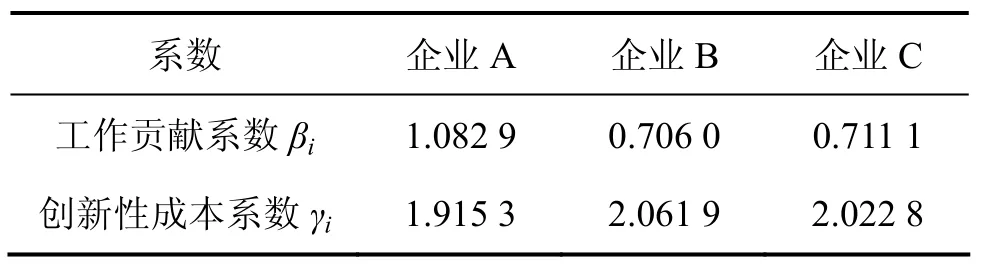
表3 企業各相關系數Table 3 Correlation coefficient of businesses

由表3可知：所有的分配比例都大于0，采用多階段博弈方法求得分配比例為：此時，企業B和C的分配比例比企業A的分配系數小很多。由表3可知：企業B和C的工作貢獻系數比企業A的小，所以，分配比例較小，但它們的創新性系數比企業A的大，相應地，所承擔的風險也較大。在一定程度上，此時的分配比例會打擊企業B和C的積極性，不利于集疏運一體化的穩定，故應對結果進行修正，以提高企業B和C的利益分配比例。利用已知數據求得特征函數并構造最小距離解，即

此為所求利益分配比例。可得A，B和C 3個企業各自所得的最終分配利益分別為3 711.6，1 066.8和1 221.6萬元。

修正后的分配比例考慮了公路企業承擔的風險，同時也兼顧了鐵路作為盟主所做出的較大貢獻。在穩定集疏運一體化的前提下鐵路企業做出一定的讓步，尋求令各成員企業都較為滿意的分配方案，較修正之前更能被企業B和C公路企業所接受。

4 結論

（1） 企業成員追求自身最大收益時所付出的工作努力水平與自身的分配系數成正比，與自身的貢獻系數成正比，與自身創新性活動的成本系數的平方成反比。

（2） 在其他企業的創新性成本系數和工作貢獻系數不變的情況下，降低自身的創新性成本系數（即相應地降低其在集疏運中所承擔的風險），提高工作貢獻系數，其分配比例會增加。

（3） 在非特殊情況下，模型中式（21）也可以作為伙伴選擇的1個條件，當創新性成本系數和工作貢獻系數滿足該式時，分配比例理論上都大于0，基本上符合集疏運的分配原則，則集疏運一體化可以繼續進行；當創新性成本系數和工作貢獻系數不滿足該式時，出現了理論上的分配比例小于0的情況，此時，分配比例小于0的企業不會選擇加入集疏運組織，導致集疏運體系不成立。

（4） 當某企業在利益分配模型中分配比例小于0而該企業有具有非常大的潛力，或者當某企業較高的創新性成本帶來的風險導致分配比例較低時，采用修正后的模型能更好地保證集疏運快速高效、合理地運行。

[1] 羅利, 魯若愚. Shapley值在產學研合作利益分配博弈分析中的應用[J]. 軟科學, 2001, 15（2）： 17?19.

LUO Li, LU Ruo-yu. Application of the Shapley value in the game model of the cooperation of enterprises, colleges and institutes[J]. Soft Science, 2001, 15（2）： 17?19.

[2] 張捍東, 嚴鐘, 王建. 對企業動態聯盟利益分配問題的思考[J]. 中國管理科學, 2006（10）： 665?668.

ZHANG Han-dong, YAN zhong, WANG Jian. Thoughts on profit distribution in enterprises dynamic alliance[J]. Chinese Journal of Management Science, 2006（10）： 665?668.

[3] 生延超. 基于改進的Shapley值法的技術聯盟企業利益分配[J]. 大連理工大學學報： 社會科學版, 2009, 30（2）： 34?39.

SHENG Yan-chao. The benefit assignment mechanism research on technical alliance based on improved Shapley value[J]. Journal of Dalian University of Technology： Social Sciences, 2009, 30（2）： 34?39.

[4] 彭育松, 周敏. 合作博弈下的共同配送利益合理分配模型[J].云南財貿學院學報, 2006, 22（1）： 60?64.

PENG Yu-song, ZHOU Ming. Profit distribution model of co-delivery under co-game[J]. Journal of Yunnan Finance and Trade Institute, 2006, 22（1）： 60?64.

[5] 王岳峰, 劉偉. 考慮權重的Shapley值法虛擬企業伙伴利益分配策略的改進[J]. 上海海事大學學報, 2005, 26（4）： 48?51.

WANG Yue-feng, LIU Wei. Innovation on strategies of profit allocation among partners in virtual enterprise based on Shapley value considering weight[J]. Journal of Shanghai Maritime University, 2005, 26（4）： 48?51.

[6] 于曉輝, 張強. 基于區間Shapley值的生產合作利益分配研究[J]. 北京理工大學學報, 2008, 28（7）： 655?658.

YU Xiao-hui, ZHANG Qiang. Profit allocation in production cooperative game based on interval Shapley value[J]. Journal of Beijing Institute of Technology： Natural Science Edition, 2008, 28（7）： 655?658.

[7] 胡霞. 虛擬企業伙伴間利益協調模式研究[D]. 大連： 大連理工大學管理與經濟學部, 2005： 27?30.

HU Xia. Research on benefit allocation mode of virtual enterprises[D]. Dalian： Dalian University of Technology. School of Management, 2005： 27?30.

[8] 穆喜產, 送素玲, 吳云燕, 等. 顧客聯盟的利益分配問題研究[J]. 軟科學, 2009, 23（1）： 127?131.

MU Xi-chan, SONG Su-ling, WU Yun-yan, et al. Study on profit distribution among customer alliance[J]. Soft Science, 2009, 23（1）： 127?131.

[9] Perng Y H, Chen S J, Lu H J. Potential benefits for collaborating formwork subcontractors based on co-operative game theory[J]. Building and Environment, 2005（40）： 239?244.

[10] 盧少華, 陶志祥. 動態聯盟企業的利益分配博弈[J]. 管理工程學報, 2004, 18（3）： 65?68.

LU Shao-hua, TAO Zhi-xian. Profit-allotting game in virtual enterprise[J]. Journal of Engineering Management, 2004, 18（3）： 65?68.

[11] 李亞東, 李從東, 張炎亮. 動態聯盟收益分配問題的博弈研究[J]. 工業工程, 2006, 9（3）： 15?18.

LI Ya-dong, LI Cong-dong, ZHANG Yan-liang. Research on the profit-allotting problem of dynamic-alliances through the game theory[J]. Industrial Engineering Journal, 2006, 9（3）： 15?18.

[12] 盧少華. 供應鏈企業的行為和利益分配研究[J]. 物流技術, 2005（4）： 54?56.

LU Shao-hua. Economic analysis of agile virtual enterprises[J]. Logistics Technology, 2005（4）： 54?56.

[13] 袁興玲. 網絡化制造聯盟的伙伴選擇和利益分配研究[D]. 武漢： 華中科技大學機械科學與工程學院, 2007： 20?36.

YUAN Xing-ling. Research on partner selection and profit allocation for global manufacturing alliance[D]. Wuhan： Huazhong University of Science and Technology. School of Mechanical Science and Engineering, 2007： 20?36.

[14] 白潔. 虛擬企業收益分配機制研究[D]. 長春： 吉林大學管理學院, 2006： 13?25.

BAI Jie. The research on virtual company income share[D]. Changchun： Jilin University. School of Management, 2006： 13?25.

[15] 陳菊紅, 汪應洛, 孫林巖. 虛擬企業收益分配問題博弈研究[J]. 運籌與管理, 2002, 11（1）： 11?16.

CHEN Ju-hong, WANG Ying-luo, SUN Lin-yan. Research on the profit distribution gaming of virtual enterprise[J]. Operations Research and Management Science, 2002, 11（1）： 11?16.

[16] 臧寧寧. 項目治理中利益相關方合作博弈關系研究[D]. 濟南：山東大學管理學院, 2008： 52?56.

ZANG Ning-ning. The research of the cooperative game among the stakeholder[D]. Ji’nan： Shandong University. School of Management, 2008： 52?56.

[17] 劉興旺. 基于博弈論的供應鏈企業收益分配問題研究[D]. 長沙： 長沙理工大學交通運輸工程學院, 2007： 7?14, 41?52.

LIU Xing-wang. Research on the income distribution problem of enterprise in supply chain based on game theory[D]. Changsha： Changsha University of Science & Technology. School of Traffic and Transportation Engineering, 2007： 7?14, 41?52.

[18] Sakawa M, Nishizaki I, Uemura Y. Fuzzy programming and profit and cost allocation for a production and transportation problem[J]. European Journal of Operational Research, 2001, 131： 1?15.

[19] Jia N X, Yokoyama R. Profit allocation of independent power producers based on cooperative game theory[J]. Electrical Power and Energy Systems, 2003, 25： 633?641.

[20] Guardiola L A, Meca A, Timmer J. Cooperation and profit allocation in distribution chains[J]. Decision Support Systems, 2007, 44： 17?27.

[21] 陳雯. 基于模糊合作對策的動態聯盟企業收益分配策略研究[D]. 北京： 北京理工大學管理與經濟學院, 2007： 40?44, 51?84.

CHEN Wen. Research on the profit allocation strategy of Virtual enterprises based on cooperative with fuzzy coalitions[D]. Beijing： Beijing Institute of Technology. School of Management and Economics, 2007： 40?44, 51?84.

[22] 趙忠華. 虛擬企業利益分配有效性評價[J]. 商業研究, 2003（2）： 60?62.

ZHAO Zhong-hua. Available evaluation on benefit allocation of virtual enterprise[J]. Commercial Research, 2003（2）： 60?62.

[23] 陳寶. 企業動態聯盟的伙伴選擇與利益分配研究[D]. 成都：四川大學工商管理學院, 2005： 40?49.

CHEN Bao. Partner select & benefit allocation research of dynamic alliance[D]. Chengdu： Sichuan University. Business School, 2005： 40?49.

[24] Tsai K M, You S Y, Lin Y H, et al. A fuzzy goal programming approach with priority for channel allocation problem in steel industry[J]. Expert Systems with Applications, 2008, 34： 1870?1876.

[25] 姜起源, 謝金星. 數學模型[M]. 3版. 北京： 高等教育出版社, 2003： 221?224.

JIANG Qi-yuan, XIE Jin-xing. Mathematical models[M]. 3rd ed. Beijing： Higher Education Press, 2003： 221?224.

（編輯 陳燦華）

Game analysis of profit distribution of railway heavy-haul cargo distribution and transportation system with asymmetric information

FENG Fen-ling, LAN Dan
（School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China）

The principles and elements of distributing interests produced in the process of cargo distribution and transportation under asymmetric information were analyzed, the profit distribution arrangement was modeled on the basis of such analysis, and the solution was obtained through gaming in multiple stages. The model was fixed by means of minimum distance solution achieved through Shapely value method based on the principle of profit sharing through consultation. The results show that the more the risk bearing in the innovation of cargo distribution and transportation, the less the profit; the more the contribution to the program, the more the profit. The risk will be shared equally and small enterprises as well as potential cooperative enterprises will be protected. Profit distribution of cargo distribution and transportation with asymmetric information can be well handled in this model, thus verifying the rationality and applicability of the model.

railway; heavy-haul transport; cargo distribution and transportation; profit distribution; game analysis

U294.1

A

1672?7207（2011）05?1473?09

2010?06?10；

2010?08?28

教育部中央高校基本科研業務費專項資金資助項目（2010QZZD021）；鐵道部科技研究開發計劃項目（2010X014，2008X020-B）

馮芬玲（1973?），女，河北邯鄲人，博士，副教授，從事交通運輸規劃與管理研究；電話：13548589469；E-mail： FFL0731@163.com