高效太陽能電池薄膜生長工藝優化模型的研究及其意義

李桂琴，陸利新，葉曉軍，李紅波，夏士偉

（1. 上海大學 機自學院，上海 200072；2. 上海空間電源研究所，上海 200241；3. 上海欣邦電氣有限公司，上海 200051）

0 引言

開發新能源和可再生清潔能源是21世紀最具決定影響的技術領域之一，太陽能光伏技術是近年來發展最快、最有活力的可再生能源利用技術。薄膜太陽能電池是第二代太陽能電池，它是是在玻璃或不銹鋼等基板上沉積幾微米厚的薄膜而成，具有成本低、能耗低、單片電池面積大等優點，便于工業化大規模生產，成為降低太陽電池成本的主要手段和發展趨勢。

薄膜的結構和性質與制備工藝的關系非常密切，目前認為以輝光放電法制備的非晶硅膜質量最好，即在輝光放電裝置中，利用反應氣體在等離子體中發生分解而在襯底上淀積成薄膜。等離子增強化學氣相沉積（Plasma Enhanced Chemical Vapor Deposition，PECVD）作為薄膜生長的核心設備，它的制備工藝條件，如襯底溫度、射頻電源的功率、工作氣壓、不同氣體的比例、氣體的流速等都對薄膜的生長速率、成分、結構、物理性能等有較大影響；另外設備的結構參數，如氣體的氣流分布均勻性和電場分布均勻性等也影響薄膜太陽電池產品的質量及生產效率。

設備的工藝水平決定著薄膜生產技術水平，而工藝參數的控制一直是PECVD設備較難解決的一個問題。國外在研究設備的同時也在為該設備的正常合理化工藝作針對性的研究。現在國產設備的成膜速率低，并且不均勻，究其原因就是在研究設備的過程當中對設備的工藝參數控制的研究不足，這就造成了制造設備企業生產的設備與工藝的脫節，有的甚至有較大程度的設計不合理。工藝穩定性根本不能保證，嚴重影響產品質量薄膜生長過程中存在多目標優化問題，如體現產品質量的薄膜均勻性、體現生長效率的鍍膜速率等，這些需求之間存在相互矛盾與制約。

薄膜生長過程最佳參數的確定需要大量的工作，過去常常通過反復試驗，或依靠經驗來解決這類問題。PECVD技術沉積薄膜的過程是一個非常復雜的物理化學過程，涉及等離子體化學反應、熱力學和動力學原理的復雜過程，已超出了平衡熱力學和動力學理論范圍[1]，是非線性、多層次、隨機的、不確定性等多種復雜特性的組合。其反應室內部電極間電場、流體場、溫度場等的分布均勻性將直接影響到薄膜沉積的均勻性。因此，面向薄膜生長控制的工藝過程建模，建立工藝參數與薄膜性能之間的定量解析關系變得極為必要，成為改進工藝、提升裝備技術水平迫切需要解決的關鍵問題。

1 薄膜設備工藝發展與薄膜生長規律研究

半導體設備的發展有兩種方式，一是通過整體技術的革新，二是通過單元技術工藝的創新。當前世界上對非晶硅及多晶硅薄膜的研究，其核心在于PECVD設備的鍍膜均勻性和鍍膜速率難以兩全的問題，國內外學者普遍發現隨著沉積速率的提高，材料質量與電池性能逐步下降[2~4]。首先薄膜沉積過程不僅與反應氣體有關，而是與反應氣體、反應產物氣體、中間產物氣體、副產物氣體、殘留氣體等的混合氣體有關。平板電極式PECVD中采用四周排氣結構，上述氣體存在一定的濃度梯度分布，導致鍍膜區域各種氣體濃度比例的非均勻分布，影響PECVD鍍膜均勻性。另外，高質量的硅薄膜生長需要有一定的條件（包括溫度、速率等）。一般來說，鍍膜速率越慢，溫度越高，晶體生長越充分，膜層質量越好。但在薄膜電池應用中既需要低溫工藝，又需要高產能，兩者之間存在矛盾和制約。

為更好地了解薄膜的生長過程，國內外學者進行了廣泛的實驗和理論研究，主要集中在薄膜生長過程的物理和化學過程的解釋、建模及控制等方面。PECVD熱力學分析可以定量描述沉積速率和沉積層組成，動力學分析研究沉積機理，即各種表面化學反應步驟的進行規律及其相互聯系[5]。研究發現等離子體光發射譜中的Si*或SiH*的發射強度正比于非晶硅或微晶硅薄膜的沉積速率[6~10]，而且光譜中Hα的強度可看作等離子中原子H濃度的表征[11]，工作氣壓與輝光功率改變時，材料的晶化率隨Hα/Si*或者Hα/SiH*的比值的下降而逐步下降[8,9]，而且當Hα/Si*比值高于某一個特定數值時，薄膜的生長發生了從非晶硅向微晶硅的轉變，而且這個比值與離子能量和沉積速率無關[10]。國內外在薄膜沉積的有限單元法、蒙特卡羅、分子動力學、量子力學模擬等方面也做了大量研究，得到比較好的效果[12~16]。E. Pleule等[17]對微波CVD金剛石沉積進行有限元數字模擬，并開發一個反應室原型系統測試仿真結果；Olivier Leroy等[18]建立二維模型模擬PECVD中的電、熱、和化學現象，并與實驗對比，獲得了較滿意的效果。中國科學院上海硅酸鹽研究所和上海交通大學通過實驗研究,得到了SiNx薄膜的生長速率隨工作壓力、氨氣與硅烷的流量比、反應溫度變化的規律[19]，You-Jae Kim[20]、王慶章[21]對薄膜工藝的氣流場進行仿真，用于改進薄膜沉積中的噴頭設計；胡貴華等[22]采用可視化方式模擬PECVD反應室內氣體的溫度場和速度場分布情況，但沒有考慮反應室內的表面化學反應；葛洪[23]等對電極間電勢分布的均勻性進行了數值模擬，獲得優化的真空電勢分布。

薄膜材料的性能與其微結構及組分密切相關，薄膜的光電特性強烈地依賴于薄膜的微結構、化學組分和雜質性質。薄膜的生長過程通常遠離平衡態，形成的隨機性很大，具有復雜的非規則微結構，如何準確地表征薄膜的非規則微結構一直是科學研究的重要課題。

分形理論是本課題研究應用的核心理論。分形理論可用于對材料顯微圖像的定量表征。建立在分維概念基礎上的分形理論是非線性科學的重要組成部分之一，在表面粗糙度的測量[24]、晶界形貌、材料斷裂機理分析、凝聚體結構等研究中都有重要應用[25]。在一些非平衡的薄膜過程中，如氣態薄膜介質中的電擊穿、液體薄膜中的晶體生長、液體街面上的電解沉積、固體薄膜中的分形晶化、培養基板上細菌群落的生長等，都出現分形生長現象。分形幾何其中心內容是指不規則幾何形體在動力學演化過程中，在一定的標度尺度范圍內相應的測度不隨尺度的改變而改變。正因為分形理論在描述自然界中復雜現象方面的獨特作用，為研究復雜問題提供了新方法，開辟了新視野。1985年Elam等首先利用電子顯微鏡獲得了沉積在840℃的石英襯底上的濺射NbGe2薄膜的分形圖形，論證了分形理論在薄膜微觀形態模擬中應用的可行性。由于薄膜表面的形貌對薄膜制成的器件的電特性產生強烈的影響，國內外學者對從分形角度對薄膜生長發生了廣泛的興趣。

計算智能（CI，Computational Intelligence ）方法是通過對不確定、不精確及不完全真值的容錯以取得低代價的解決方案和魯棒性，近年來，越來越多的學者把傳統理論與人工智能技術相結合，對復雜系統進行智能化控制。神經網絡系統是一個具有高度非線性的超大規模連續時間動力系統[25]，遺傳算法的整體搜索策略和優化搜索方法，提供了一種求解復雜系統問題的通用框架，對問題的種類有很強的魯棒性，模糊控制適合于不確定分布參數、非線性、多輸入多輸出、時變等復雜系統的控制問題。將三者結合是智能控制研究的主要方向之一。Hong S.等[26]分析了半導體制造過程中的物理化學現象，指出蒙特卡羅模擬等方法計算量大、對宏觀效果的描述有限，經驗方法包括統計實驗設計等的精確性受到質疑，認為神經網絡的精度和魯棒性都優于統計方法，并采用發射光譜數據建立神經網絡對離子蝕刻反應建模，結果與測試數據達到很好的一致性。Byungwhan Kim等[27]應用遺傳算法優化廣義回歸神經網絡來預測等離子增強沉積過程，與一般的廣義回歸神經網絡和統計回歸模型對比，表現出更顯著的預測效果。山東大學[28]利用人工神經網絡建立了工藝條件和Si3N4 薄膜的顯微硬度關系模型，用遺傳算法優化制備薄膜的工藝參數。P.Melin和Casillo.O[29,30]將混合智能系統用于復雜電化學制造工藝控制、神經-模糊-分形方法用于非線性生物化學反應器中非穩態行為的控制等。

2 薄膜生長工藝優化模型

圖1 神經網絡與遺傳算法集成的多目標優化模型

將神經網絡與分形理論相結合，充分利用神經網絡非線性映射、計算能力、自適應等優點，大大地減少傳統實數域分形維數的計算量，能夠取得更好的效果。模糊邏輯和神經網絡結合建立的模糊神經網絡，能夠對輸入值進行判斷選擇, 如果所提供的輸入變量是無效的, 它就會在訓練過程中自動被丟棄，同時在得到輸出值的同時生成規則集。遺傳算法能夠對神經網絡學習規則實現自動優化，從而提高學習速率；其全局優化及隱含并行性的特點能夠提高權系數優化速度，解決復雜系統中神經網絡學習難的問題。 當用遺傳算法進行優化時，其最大的難題就是需要一個適應度函數來評估優化的結果，利用神經網絡作為遺傳算法的適應度函數進行處理，無需為遺傳算法建立一個新的適應度函數，這種方法對于解決適應度函數難以獲得的問題和提高計算效率非常有效（如圖1所示）。因此，將它們有機結合和集成，把分維和材料性能及制備工藝（如制備薄膜的溫度和時間）相聯系，即找到定量關系式，進而通過分形研究來改善材料性能，找到最佳制備工藝，解決成膜質量和鍍膜速率難以兩全的問題。圖2為模型總體結構圖。

首先，以PECVD設備為主要實驗手段，結合已有的等離子體反應、氣體反應和表面化學反應生長機理，使用數據驅動與反應機理融合的混合模型作為逼近實際非線性過程的模型，以提高模型的預測性能。

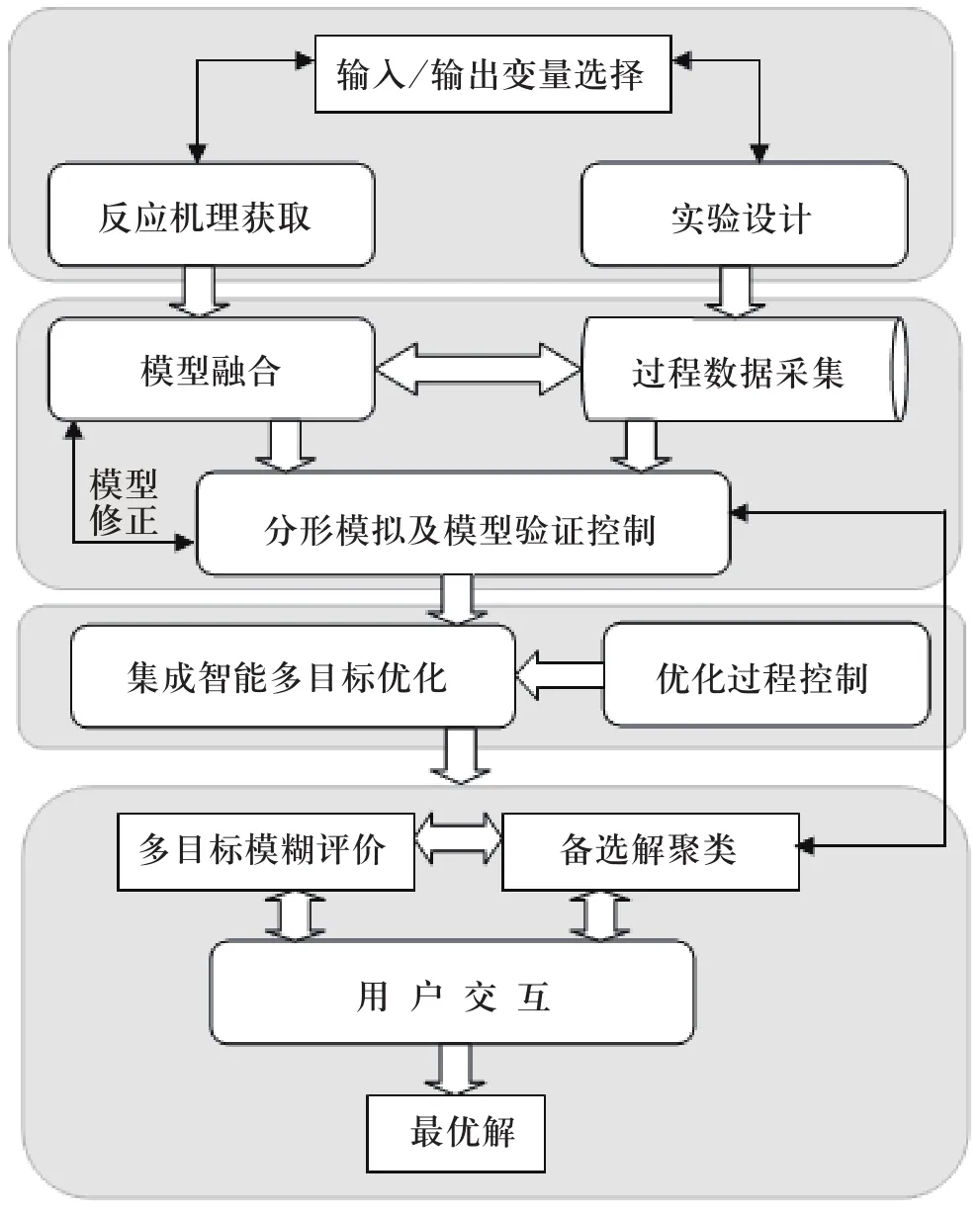
圖2 模型總體結構圖

其次，采用玻璃襯底或不銹鋼柔性襯底沉積納米硅/微晶硅薄膜，分別選擇相同和不同的試件重復薄膜生長實驗；通過采用正交實驗等方法改變主要工藝條件，確定薄膜生長的主要影響參量；測試和獲得不同試驗條件和不同試驗階段的分形圖像及其性能參數（厚度、折射率等）。

然后，通過實驗結果的分析與比較，對分形與計算智能集成的理論和算法進行測試與驗證；并根據實驗與模擬結果對比，若存在不一致情況，找出影響因素，修正計算模型。

最后，建立新型的決策分析系統，將集成系統的輸出結果進行自動分析、決策，并將結果用于指導太陽能電池薄膜生長過程控制。

3 結束語

提出一種用于太陽能電池薄膜生長的工藝建模方法，采用的計算智能技術與分形方法綜合集成的方法：計算智能技術用來生成混合智能系統，分形理論提供數學工具來模擬自然對象的幾何復雜性，采用分形維數技術，用于識別和系統建模過程，從而為PECVD設備制造和PECVD鍍膜工藝提供一定的理論指導依據，使設備工藝更符合生產的要求；另外，在PECVD設備的設計階段就考慮其使用的工藝要求，可使PECVD設備的生產與使用工藝不脫節，從而為規模生產鋪路，能夠推動裝備的研究與應用開發，提高智能制造水平。

[1] Fischer-Cripps A C.Nanoindentation.New York:Spring-Verlag,Inc.2002.

[2] B.Rech,T.Roschek,T.Repmann,et al.Microcrystalline Silicon for Large Area Thin Film Solar Cells.Thin Solid Films,2003,427:157-165.

[3] M.Kondo,S.Suzuki,Y.Nasuno,et al.Recent Development in the High Growth Rate Technique of Device-Grade Microcrystalline Silicon Thin Film. Plasma Sources Sci.Technol.2003,12(4):S111-S116.

[4] C.Niikura,M.Kondo,A.Matsuda. Preparation of Microcrystalline Silicon Films at Ultra High-Rate of 10nm/S Using High-Density Plasma,J.Non-Cryst.Solids,2004,338-340(15):42-46.

[5] G.Y.Meng,H.Z.Song, H.B.Wang,et al.Progress in ion-transport inorganic membranes by novel chemical vapor deposition(CVD)techniques,Thin Solid Films,2002,409(1):105-111.

[6] A.Matsuda,T.Kaga, H. Tanaka,et al.Glow-Discharge Deposition of a-Si:H from Pure Si2h6 and Pure Sih4,Jpn.J.Appl.Phys.,1983,22:L115-L117.

[7] A.A.Howling,J.-L.Dorier,Ch.Hollenstein, et al. Frequency Effect in Silane Plasmas Enhanced Chemical Vapor Deposition,J.Vac.Sci.Technol.1992,10(4):1080-1085.

[8] H.Keppner,J.Meier, P.Torres,et al.Microcrystalline Silicon and Micromorph Tandem Solar Cells.Appl.Phys.A:Mater.Sci.Process.1999,69(2):69.

[9] L.Guo,M.Kondo,M.Fukawa,Etal.High Rate Deposition of Microcrystalline Silicon Using Conventional Plasma Enhance Chemical Vapor Deposition,Jpn.J.Appl.Phys.1998,37:L1116-L1118.

[10]J.K.Rath,R.H.J.Franken,A.Gorgijn,et al.Growth Mechanism of Microcrystalline Silicon at High Pressure Conditions,J.Non-Cryst.Solids,2004,338-340(15):56-60.

[11]M.Heintze,R.Zedlitz,.H.Bauer.Analysis of High-Rate a-Si:H Deposition in a VHF Plasma,J.Phys.D:Appl.Phys.1993,26:1781-1786.

[12]宋鵬,陸建生,周潔,等.影響金屬薄膜沉積初期因素的有限單元法模擬[J].材料科學與工藝,2007,15(2):290-293.

[13]王恩哥.薄膜生長中的表面動力學[J].物理學進展,2003,(1):1-61,

[14]鄭小平,張佩峰,范多旺.擴散理論對RLA模型中交換作用的研究[J]. 物理學報,2008(1):425-429.

[15]Meixner M,Kunert R,Scholl E. Control of strain-mediated growth kinetics of self-assembled semiconductor quantum dots. Phys Rev B,2003,67(19):195301.

[16]A.F.Bower,E.Chason,L.B.Freund,et al.Self-organization in strained heteroepitaxial nanostructures:multi-scale modeling,simulation and experiment.NSF Nanoscale Science and Engineering Grantees Conference,2003,Dec 16-18.

[17]E.Pleuler,C.Wild,et al,The CAP-reactor,a novel microwave CVD system for diamond deposition, Diamond and Related Materials,2002,(11):467-471.

[18]Olivier Leroy,Gérard Gousset,Luís Lemos Alves,et al.Twodimensional modeling of SiH4-H2 radio-frequency discharges for a-Si:H deposition. Plasma Sources Science and Technology,1998,3(7):348-358.

[19]劉學建,金承鈺,黃智勇,等.工藝因素對低壓化學氣相沉積氮化硅薄膜的影響[J].硅酸鹽學報,2003,31(10):986-990.

[20]王慶章,趙庚申,許盛之,等.薄膜工藝中的系統仿真研究[J].南開大學學報(自然科學版),2006,39(6):45-48.

[21]You-Jae Kim,Jin-Hyo Boo,Byungyou Hong,et al.Effects of showerhead shapes on the flowfields in a RF-PECVD reactor.Surface & Coatings Technology,2005,193(1-3):88-93.

[22]胡貴華,朱文華,俞濤,等. PECVD 熱流場數值模擬的可視化研究[J].系 統 仿 真 學 報,2008,20(21):5885-5889.

[23]葛洪,張曉丹,岳強,等.大面積VHF-PECVD用多點饋入平行板電極饋入點優化的數值研究[J].真空科學與技術學報,2008,28(4):281-285.

[24]Schmahling J A,Hamprecht F A,Hoffmann D M P.Three-dimensional measure of surface roughness based on mathematical morphology.International Journal of Machine Tools and Manufacture,2006,46(14):1764-1769.

[25]魏諾.非線性科學基礎與應用[M].北京:科學出版社,2004.

[26]Hong S.,May G.,Park D.Neural Network Modeling of Reactive Ion Etch Using Optical Emission Spectroscopy Data.IEEE Trans.Semi.Manufac.2003,16(4):598-608.

[27]Byungwhan Kim,Dukwoo Lee,Seung Soo Han. Prediction of Plasma Enhanced Deposition Process Using GA-Optimized GRNN.Advances in Neural Networks,ISNN 2006(2):1020-1027.

[28]張勤儉,吳春麗,李敏,等.人工神經網絡—遺傳算法優化激光—等離子體化學氣相沉積Si3N4薄膜制備工藝[J].陶瓷學報,2002,23(2):116-118.

[29]P.Melin,O.Castillo,Controlling complex electrochemical manufacturing processes with hybrid intelligent systems.Proceedings of the North American Fuzzy Information Processing Society,Atlanta,GA,2000:490-494.

[30]P.Melin,O.Castillo.Controlling Chaotic and Unstable Behavior in Non-Linear Biochemical Reactors by Using a New Neuro-Fuzzy-Fractal Approach. The Ninth IEEE International Conference on Fuzzy Systems,2000.2:949-952.