認知不確定性的諧波齒輪減速器可靠性分析研究

杜 麗，肖寧聰，黃洪鐘，何俐萍，李海慶

(電子科技大學機械電子工程學院 成都 611731)

隨著航天技術的發展，高可靠及長壽命航天產品已成為共同需求和發展趨勢。目前，在航天器設計中，一般均要求其可靠工作時間為10年、15年甚至20年以上，對航天器可靠性分析和設計提出了嚴峻的挑戰。

太陽翼驅動機構和天線指向機構是衛星的常用機構[1]。由于諧波齒輪減速器具有承載能力高、質量輕、回差低(或是接近零回差)、減速比范圍大等特點[2-3]，被廣泛地應用于太陽翼驅動機構和天線指向機構中。諧波齒輪減速器的可靠性在一定程度上決定了驅動機構和指向機構的可靠性。

目前，國內外已經對諧波齒輪減速器的運動原理、運動精度、建模等[2,4]進行了廣泛研究。然而，對諧波齒輪減速器進行壽命估計時，國內外的相關設計手冊大多將影響諧波齒輪壽命的相關參數設為固定值[5]，這可能會帶來極大的誤差。如諧波齒輪減速器的額定輸出力矩通常在某個值的周圍變動，從而允許在某些情況下輸出力矩可以發生改變。此外，航天器中使用的諧波齒輪減速器運行環境惡劣，且初始數據中通常包含著大量的主觀信息。綜上所述，單純的基于概率(隨機)的可靠性分析方法已不能很好地解決這類實際工程問題，需要一種能同時考慮認知不確定性和客觀不確定性的可靠性分析方法。

近10余年來，有關學者研究并考慮認知不確定性和客觀不確定性的可靠性分析方法。文獻[6]提出了一種區間變量及隨機變量同時存在時基于一階可靠性方法(first order reliability method，FORM)的統一不確定性分析方法。文獻[7]提出了在混合變量下的系統可靠性分析方法，用模糊數描述系統認知不確定性。然而，這些方法在處理方式和求解效率方面尚存在著許多不足。本文以航天器中使用的諧波齒輪減速器為研究對象，應用區間分析，提出一種同時處理認知不確定性和客觀不確定性的系統可靠性建模方法。為了說明該方法的有效性，采用蒙特卡羅洛仿真方法(Monte Carlo simulation, MCS)進行驗證，并對模型中的參數進行靈敏度分析。

1 不確定信息的表示和運算

1.1 基于概率的客觀不確定性表示

在實際工程中，不確定性信息隨處可見。在可靠性分析中，不確定性信息主要分為客觀不確定性和認知不確定性兩大類[8]。客觀不確定性是事物固有的、本質上的不確定性，可以用概率方法如分布函數等來描述，這類不確定性是不能消除的。

1.1.1 貝葉斯估計

設隨機矢量X的概率密度函數為f(X)，f(X)屬于概率密度函數空間fΘ，其定義為：

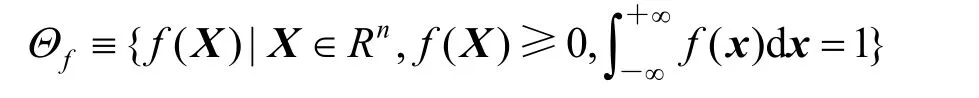
設某隨機參數θ的先驗密度為π()θ，隨機變量X的聯合密度函數為p(x|)θ，則參數θ的后驗密度函數[9]為：

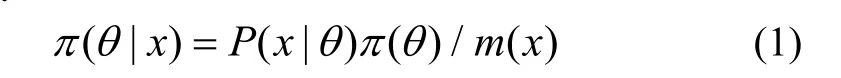
式中，m(x)為邊緣密度函數。

由于m(x)不依賴于θ，在計算θ的后驗分布中僅起到一個正則化因子的作用，如果把m(x)省略，則貝葉斯公式[9]改寫為：

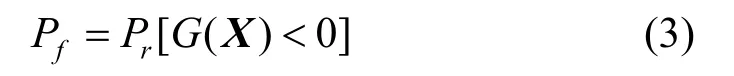
式中，G(X)為系統功能函數；X為系統隨機矢量。設隨機矢量的聯合概率密度函數為f()

式中，∝為不依賴于θ的常數因子。

1.1.2 一階可靠性方法(FORM)

在可靠性分析中，系統的失效概率定義為：XX，則系統失效概率為：

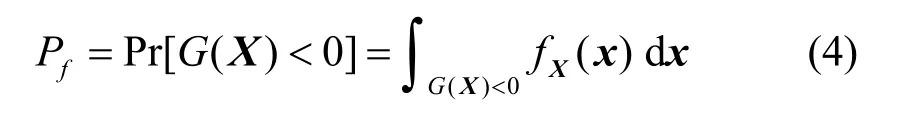
一般情況下，直接用式(4)進行求解是不可行的。用FORM計算系統的失效概率分為[10]：

式中，Φ(i)為標準正態累積分布函數。

用FORM求解系統的可靠度，主要為搜索極限狀態方程的MPP點。而MPP點搜索是一個循環迭代的優化過程，需要大量的計算時間。在某些時候，極限狀態方程可靠性設計點不只一個，或是根本搜索不到該方程的設計點。另外，如果功能函數的非線性高，形式復雜，求解其導數是非常繁瑣的。而基于樣本的仿真法，對極限狀態方程沒有特別要求，也不要求功能函數存在導數，更不需要搜索極限狀態方程的MPP點，因此，在求解算法上具有一定的便利性和很好的魯棒性。由于對系統失效貢獻最大的樣本點為MPP點和在極限狀態方程邊界周圍的點[12]，故在選擇樣本點時，僅考慮在極限狀態方程周圍的點就可以使以下方程成立，有：

1.2 基于區間的認知不確定性表示

認知不確定性也稱為主觀不確定性，處理認知不確定性常用的分析方法主要有貝葉斯方法、可能性理論、證據理論、區間方法和不精確概率等。由于區間方法的直觀性和方便性，本文擬采用區間來表示認知不確定性。

一個有界的區間可以表示為：

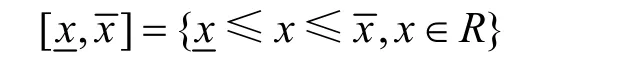
常用的區間運算通常包括并運算、平均運算、權值混合運算3種。

2 概率-非概率可靠性混合模型

2.1 基于區間分析的可靠性模型

2.2 概率-非概率可靠性混合模型

3 航天器用諧波齒輪減速器可靠性分析

3.1 諧波齒輪減速器的組成及傳動原理

諧波齒輪減速器由波發生器(wave generator)、柔輪(flexspline)和剛輪(circular spline)等3個基本構件組成[3]，如圖2所示。

諧波齒輪減速器利用柔性元件的彈性變形轉換傳遞運動和力矩。柔輪在凸輪的作用下產生變形，從而使波發生器長軸兩端的柔輪輪齒與剛輪輪齒完全嚙合，而短軸處輪齒完全脫開。在波發生器短軸和長軸之間，有的輪齒逐漸進入嚙合狀態，成為嚙入；有的逐漸進入脫開狀態，成為嚙出。由于波發生器連續轉動，使嚙入、嚙合、嚙出、脫開4種情況依次變化，從而實現減速器連續轉動[3]。

圖2 諧波齒輪減速器組成示意圖

3.2 諧波齒輪減速器可靠性建模

通常情況下，諧波齒輪減速器的壽命主要由柔輪決定，諧波齒輪減速器的壽命估計為[5]：

式中，Lh為預計壽命；TH為額定輸出轉矩；NV為實際輸入轉速；T為輸出軸名義轉矩；KA為工況系數。

根據應力-強度干涉模型，諧波齒輪減速器的功能函數為：

當G>0時，系統可靠；當G<0時，系統失效。系統的極限狀態方程為G=0。

3.3 混合模型的可靠性分析

4 可靠性靈敏度分析

可靠性靈敏度定義為失效概率對均值和方差的偏導數，它反映了隨機變量的均值和方差對結構可靠性的影響程度[13]。當隨機變量均服從正態分布時，變量Xi的可靠性靈敏度[10]為：

靈敏度分析結果能夠為可靠性設計提供指導，使設計人員明確某個參數對系統失效概率的影響最大。當靈敏度為正數時，參數變大將導致系統失效概率變大，為負數時，則參數變大會導致系統失效概率變小，所以在設計時要嚴格控制靈敏度為正的大參數的變化范圍。

5 算例仿真

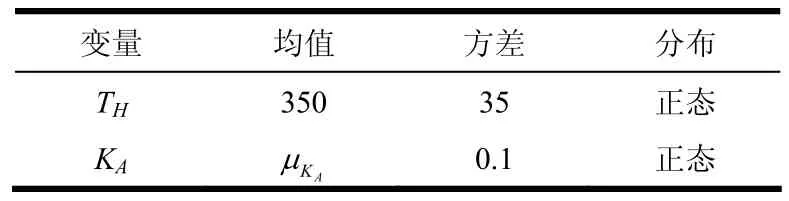
表1 諧波齒輪減速器的參數分布

表2 諧波齒輪減速器參數估計及其運算結果

表3 諧波齒輪減速器失效概率上下界隨時間變化關系

由表3可知，當設計壽命為15年時，采用壽命估算式(17)中各參數為固定值對諧波齒輪減速器進行可靠性分析，得出系統可靠的結論；然而在同時考慮認知不確定性和客觀不確定性時，得出系統的最大失效概率為0.436，最小失效概率為0.079。

為了估計本文方法的計算精度和驗證該方法的正確性，本文采用大樣本蒙特卡羅仿真方法對其進行驗證，其樣本量為106。通過仿真，得到計算結果的最小誤差為0.001，最大誤差為0.014，其系統失效概率上下界與可靠度上下界及其蒙特卡羅仿真結果如圖3和圖4所示。圖中，本文提出的方法(proposed method)記為PM，蒙特卡羅仿真記為MCS。

由圖3和圖4可知，本文所提出的方法與大樣本蒙特卡羅模擬得出的結果非常接近。然而，蒙特卡羅模擬法一般需要較多的樣本數據才能得出較為準確的結果，同時需要花費大量的計算時間，消耗大量的計算資源；而本文所提出的方法只需要少量的重要樣本點就可以較精確地得出系統極限狀態方程的近似線性超平面方程。當表2中的區間變量取并運算時，其計算和仿真結果與區間變量取平均運算時一致，不再贅述。

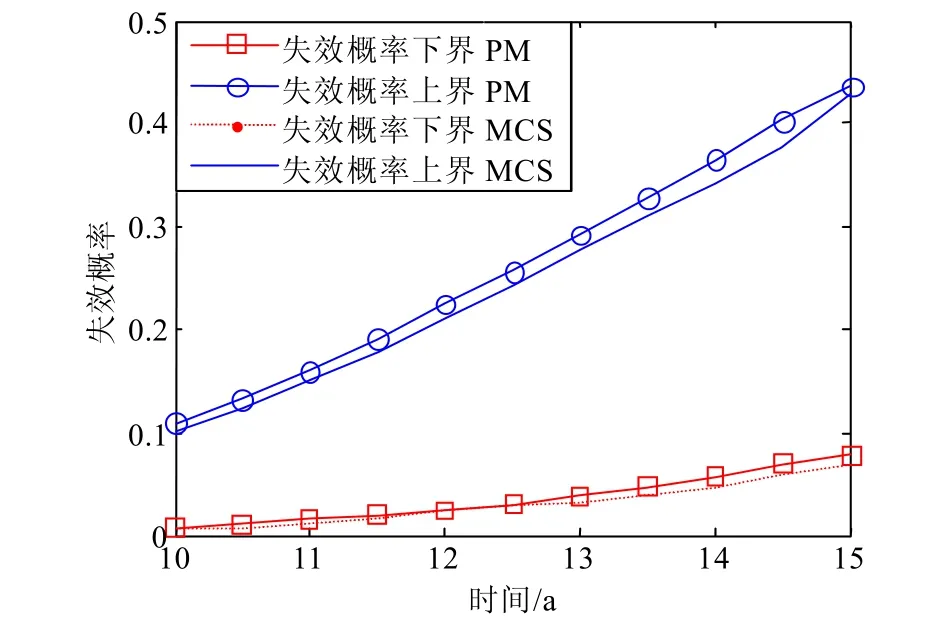
圖3 用蒙特卡羅和本文方法得出的系統失效概率的對比圖

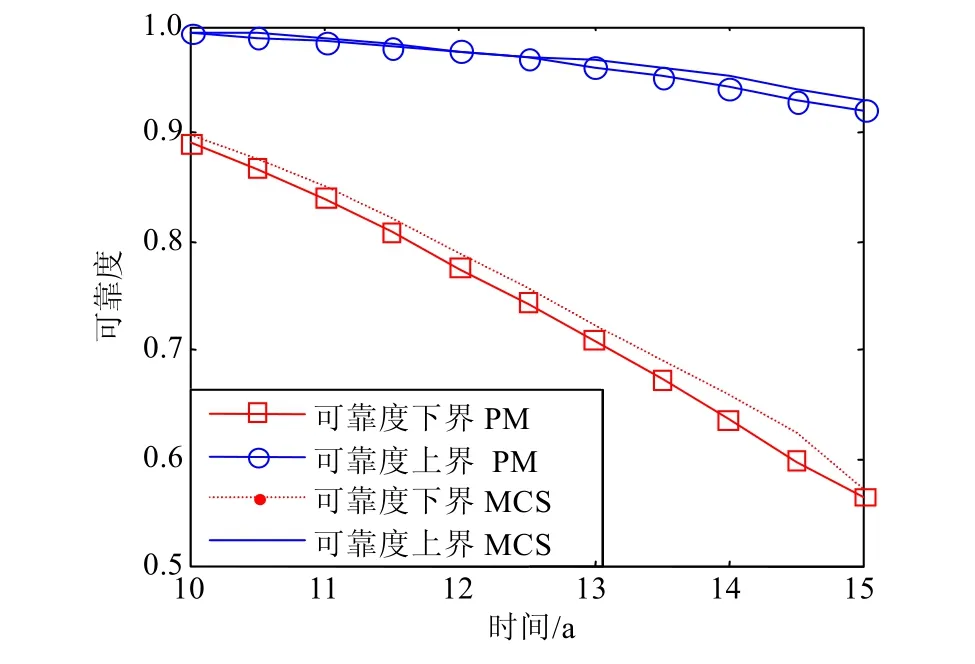
圖4 用蒙特卡羅和本文方法得出的系統可靠度的對比圖

諧波齒輪減速器可靠性靈敏度分析的計算結果如表4所示。由表4可知，各參數的靈敏度計算結果隨壽命的變化非常小，而且一旦確定了可靠性模型和參數分布概率密度函數，參數的靈敏度就是一個不變的值。從分析結果可知，參數中實際輸入轉速對系統的可靠性影響最大。

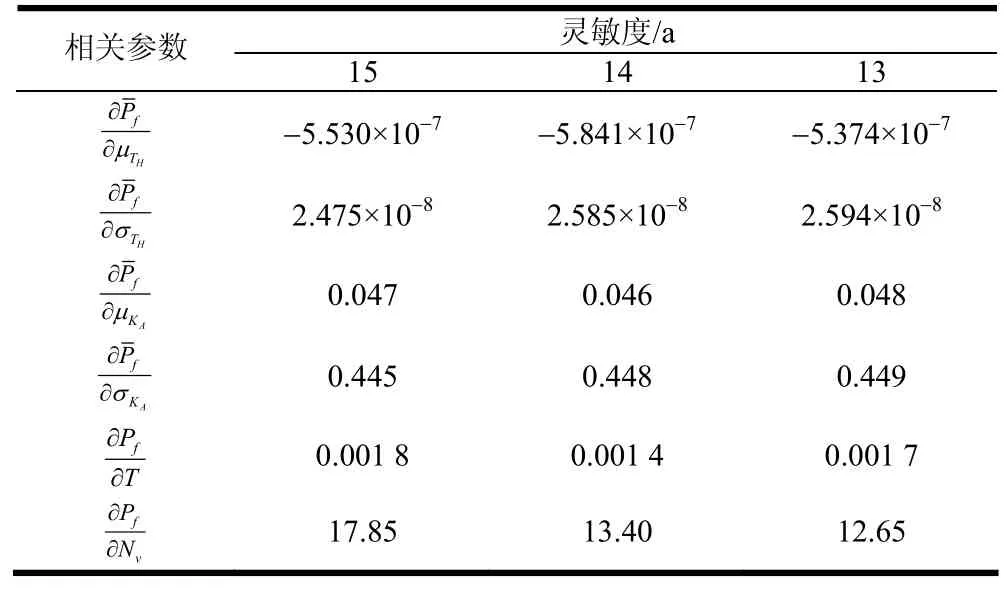
表4 諧波減速器相關參數靈敏度計算結果

6 結 論

本文介紹了不同信息來源的不確定性的處理辦法，研究了認知不確定性和客觀不確定性同時存在時的概率-非概率可靠性混合模型，建立了航天器用諧波齒輪減速器的可靠性分析模型，并對模型中的參數進行了靈敏度分析。由于認知不確定性的影響，諧波齒輪減速器隨時間變化的可靠度和失效概率是一個區間而不是一個精確的值。當區間變量和隨機變量同時存在時，搜索方程MPP點是一個雙重優化迭代過程，需要大量的計算資源和時間，在某些時候，方程的可靠性設計點不只一個，有時甚至根本搜索不到MPP點。因此，基于搜索MPP點的可靠性分析方法的效率和魯棒性都不高。由于本文所提出的方法不用搜索極限狀態方程的MPP點，因此有較高的計算效率和魯棒性。該方法可以推廣到其他領域的可靠性分析中。

[1] 屠善澄. 衛星姿態與動力學控制[M]. 北京: 中國宇航出版社, 2006.

TU Shan-cheng. Satellite attitude and dynam ic control[M].Beijing: China Astronautic Publishing House, 2006.

[2] GHORBEL F H, GANDI P S, ALPETER F. On the kinematics error in harmonic drive gears[J]. Journal of Mechanical Design, 2001, 123(1): 90-97.

[3] 周暉, 溫慶平, 張偉文. 諧波減速器在空間飛行器中的應用[J]. 真空與低溫, 2004, 10(4): 187-192.

ZHOU Hui, WEN Qing-ping, ZHANG Wei-wen. Harmonic drive used in spacecraft[J]. Vacuum & Cryogenics, 2004,10(4): 187-192.

[4] TAGHIRAD H D, BELANGER P R. Modeling and parameter identification of harmonic drive systems[J].Journal of Dynamic Systems, Measurement and Control,2009, 120(4): 439-444.

[5] 張黎驊, 鄭嚴. 新編機械設計手冊[M]. 北京: 人民郵電出版社, 2008.

ZHANG Li-hua, ZHENG Yan. New machine design handbook[M]. Beijing: People Posts & Telecomunications Publishing House Press, 2008.

[6] DU X. Unified uncertainty analysis by the first order reliability method[J]. Journal of Mechanical Design, 2008,130(9): 1-10.

[7] ADDURI P R, PENMETSA R C. System reliability analysis for mixed uncertain variables[J]. Structural Safety, 2009,31(5): 375-382.

[8] KIUREGHIAN A D. Analysis of structural reliability under parameter uncertainties[J]. Probabilistic Engineering Mechanics, 2008, 23(4): 351-358.

[9] 茆詩松. 貝葉斯統計[M]. 北京: 中國計量出版社, 1999.

MAO Shi-song. Bayesian statistics[M]. Beijing: China Metrology Publishing House, 1999.

[10] GUO J, DU X. Reliability sensitivity analysis w ith random and interval variables[J]. International Journal for Numerical Methods in Engineering, 2009, 78(13):1585-1617.

[11] MELCHERS R E. Structural reliability analysis and prediction[M]. 2nd ed. New York: Wiley, 1999.

[12] MELCHERS R E, AHAMMED M. A fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability[J]. Computers and Structures, 2004,82(1): 55-61.

[13] LU Z Z, SONG S F, YUE Z F, et al. Reliability sensitivity method by line sampling[J]. Structural Safety, 2008, 30(6):517-532.

[14] 郭書祥, 呂震宙, 馮元生. 基于區間分析的結構非概率可靠性模型[J]. 計算力學學報, 2001, 18(1): 56-60.

GUO Shu-xiang, Lü Zhen-zhou, FENG Yuan-sheng. A non-probabilistic model of structural reliability based on interval analysis[J]. Chinese Journal of Computational Mechanics, 2001, 18(1): 56-60.

[15] 郭書祥，呂震宙. 結構可靠性分析的概率和非概率混合模型[J]. 機械強度, 2002, 24(4): 524-526.

GUO Shu-xiang, Lü Zhen-zhou. Hybrid probabilistic and non-probabilistic model of structural reliability[J]. Journal of Mechanical Strength, 2002, 24(4): 524-526.

[16] 邱志平, 王曉軍. 結構靈敏度分析的區間方法[J]. 兵工學報, 2005, 26(6): 798-802.

QIU Zhi-ping, WANG Xiao-jun. An interal method for sensitivity analysis of structures[J]. Acta Armamentarii,2005, 26(6): 798-802.

編 輯 黃 莘