PSO算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的EIT圖像重建算法

謝莉莉，汪 鵬，陳 麗

XIE Li-li1，WANG Peng2，CHEN Li3

（1.天津職業(yè)大學(xué) 電子信息工程學(xué)院，天津 300410；2.河北工業(yè)大學(xué) 計算機科學(xué)與軟件學(xué)院，天津 300401；

3.河北工程大學(xué) 信息與電氣工程學(xué)院，邯鄲 056038）

0 引言

電阻抗成像（EIT）是利用對物體表面的電測量來重建反映物體內(nèi)部結(jié)構(gòu)及功能變化圖像的一種新穎的計算機影像技術(shù)。EIT在工業(yè)監(jiān)測、無損探傷等方面也引起工業(yè)界極大關(guān)注[1]。EIT的實現(xiàn)一般是通過在物體表面設(shè)置一定數(shù)量的電極，在選定的電極上施加一定模式的電流，然后測量各電極的電壓，再將這些已知的電流、電壓數(shù)據(jù)，依據(jù)圖象重建算法，構(gòu)造出物體內(nèi)部的未知阻抗圖像[2]。

我們構(gòu)造了一套實時電阻抗成像的實驗系統(tǒng)，系統(tǒng)具有32個電極，采用相鄰電極注入電流及相鄰電極測量電壓采集。如圖1所示，不同模式的電流由恒流源通過多路選擇開關(guān)施加到物體表面電極，由高精度的A/D采集模塊通過多路選擇開關(guān)采集各相鄰電極的電壓數(shù)據(jù)，最后由微控制器（51單片機）將數(shù)據(jù)預(yù)處理并控制傳輸給計算機，再重建出阻抗分布圖像。

圖1 采集系統(tǒng)結(jié)構(gòu)圖

EIT圖象重建是一個高度病態(tài)、非線性的反問題，它是目前EIT技術(shù)中關(guān)鍵的研究課題。目前成像算法主要分為基于非迭代的線性動態(tài)成像和基于迭代的非線性靜態(tài)成像兩類[3]。最早由Barber和 Brown提出的反投影重建算法，是目前唯一應(yīng)用于臨床的算法，盡管這種算法有很好的魯棒性，但成像分辨率和對比度太差。Newton-Raphson法是基于非線性迭代的靜態(tài)成像技術(shù)，被普遍認為是目前EIT圖像重建最有成效的方法，但是這些方法實現(xiàn)起來相當(dāng)復(fù)雜，成像速度慢，達不到臨床成像的要求。另外有文獻提出了基于線性神經(jīng)網(wǎng)絡(luò)的成像方法，但這些方法不能適應(yīng)EIT中復(fù)雜的病態(tài)非線性特性。有些文獻提出了基于BP神經(jīng)網(wǎng)絡(luò)的成像方法，但由于BP網(wǎng)絡(luò)本身的缺點造成成像速度慢，成像效果不佳。

基于PSO優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的方法進行EIT圖像重建是在基本BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的基礎(chǔ)上，再引入PSO算法進行權(quán)值修正。不僅能很好地適應(yīng)EIT的病態(tài)非線性特性，而且可以克服基本BP算法收斂速度慢和易陷于局部極值的局限。該方法較好地提高了BP神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)能力及泛化能力。

1 EIT圖像重建數(shù)學(xué)模型

如圖2所示，在二維場中，設(shè)被測物場區(qū)域為D，D的邊界為?D。D內(nèi)阻抗分布為ρ（x，y），電位分布為 φ（x，y），由于場內(nèi)沒有電流源和電流匯，滿足Laplace方程[4]：

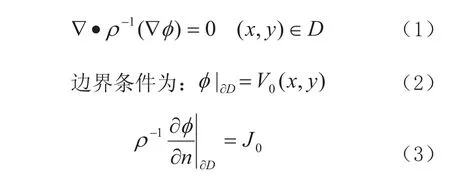
公式中 為Laplace 算子，V0為邊界處的測量電壓，J0為邊界處的電流密度，?D為區(qū)域邊界，n是邊界外法線方向。EIT問題就是從已知邊界處的J0和V0求解阻抗分布ρ。它是一個非線性的反問題，在求解反問題的過程中又涉及到求解正問題。所謂正問題就是已知阻抗分布ρ和激勵電流模式J0計算出電位分布φ。在現(xiàn)有的EIT圖象重建方法中對正問題的求解均借助于有限元方法（FEM），對反問題的求解通常使用迭代的方法。

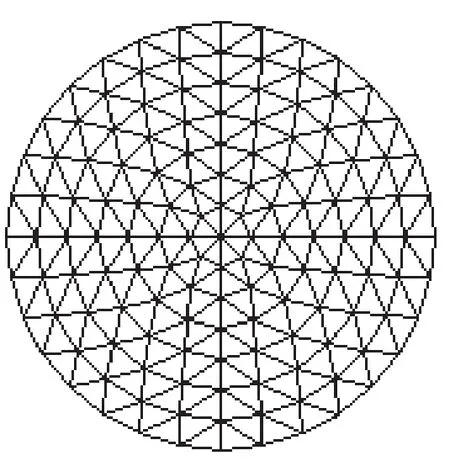
圖2 圓形樣品

2 BP-PSO實現(xiàn)EIT圖像重建

BP（Back Propagation）網(wǎng)絡(luò)是1986年由Rumelhart和McCelland為首的科學(xué)家小組提出，是一種按誤差逆?zhèn)鞑ニ惴ㄓ?xùn)練的多層前饋網(wǎng)絡(luò)，是目前應(yīng)用最廣泛的神經(jīng)網(wǎng)絡(luò)模型之一。BP網(wǎng)絡(luò)能學(xué)習(xí)和存貯大量的輸入-輸出模式映射關(guān)系，而無需事前揭示描述這種映射關(guān)系的數(shù)學(xué)方程。它的學(xué)習(xí)規(guī)則是使用最速下降法，通過反向傳播來不斷調(diào)整網(wǎng)絡(luò)的權(quán)值和閾值，使網(wǎng)絡(luò)的誤差平方和最小。BP神經(jīng)網(wǎng)絡(luò)模型拓撲結(jié)構(gòu)包括輸入層（input）、隱層（hide layer）和輸出層（output layer）。

粒子群算法（Particle Swarm Optimization，PSO）是模擬鳥類覓食行為的一種啟發(fā)式搜索方法[5]。PSO算法使用下面公式（7）和（8）更新空間位置和速度。每代粒子根據(jù)適應(yīng)度函數(shù)得到最優(yōu)粒子，經(jīng)過若干次迭代后最優(yōu)粒子即為所求最優(yōu)解。

2.1 神經(jīng)網(wǎng)絡(luò)構(gòu)造及參數(shù)設(shè)置

將圓形樣品均勻剖分成7層，如圖2所示，共141個節(jié)點、248個單元。最外層有32個節(jié)點，將32個電極均勻放置在外層32個節(jié)點上。采用相鄰電極驅(qū)動及相鄰電極測量，進行32輪電流注入，每輪可獲得29個獨立邊界電壓，共928個數(shù)據(jù)。

根據(jù)圖3所示的網(wǎng)絡(luò)結(jié)構(gòu)，設(shè)置網(wǎng)絡(luò)，928個測量數(shù)據(jù)對應(yīng)輸入層的輸入信息個數(shù)m，248個單元對應(yīng)輸出層的輸出信息個數(shù)q。設(shè)置隱含層節(jié)點個數(shù)n為248個。連接權(quán)值和閾值學(xué)習(xí)參數(shù)α＝ β＝0.6。PSO搜索空間維數(shù)（BP網(wǎng)絡(luò)權(quán)值和閾值數(shù)目）：D＝m×n＋n×q＋n＋q。PSO算法的最小適應(yīng)度（最小訓(xùn)練停止誤差）γ＝10－6；PSO的學(xué)習(xí)因子c1＝c2＝2；慣性權(quán)值u＝1.0；PSO算法初始群體個體數(shù)目設(shè)為50；最大迭代遍數(shù)T＝1000；PSO初始樣本生成：隨機初始化50*D個初始值。

2.2 神經(jīng)網(wǎng)絡(luò)樣本的產(chǎn)生

隨機生成100個樣本，每個樣本的期望輸出采用有限元法計算。先隨機生成每個樣本的輸出（248個單元的電導(dǎo)率），再利用有限元法計算出928個邊界電壓值，作為一個樣本。

2.3 用PSO訓(xùn)練神經(jīng)網(wǎng)絡(luò)過程

根據(jù)神經(jīng)網(wǎng)絡(luò)輸出層單元的新激活值計算公式計算出每個粒子坐標所對應(yīng)的神經(jīng)網(wǎng)絡(luò)的輸出O，假設(shè)期望輸出為A（O 和A均為q×1維向量），代入適應(yīng)度函數(shù)：

式中，Ok和Ak分別為輸出層第k個單元的實際輸出值和期望輸出值。

PSO算法優(yōu)化的目標，就是找到這樣一個粒子坐標（BP神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值），使得適應(yīng)度函數(shù)得到最小值。

POS算法的過程為：首先初始化粒子群坐標Xi和速度Vi；初始化Pi＝Xi。根據(jù)公式（4）計算所有粒子的適應(yīng)度，并將取得最小適應(yīng)度的粒子坐標付給Pg。

3 重建圖像及結(jié)論

根據(jù)以上論述建立BP神經(jīng)網(wǎng)絡(luò)，用PSO算法對網(wǎng)絡(luò)權(quán)值和閾值進行優(yōu)化訓(xùn)練，重建圓形樣品的電導(dǎo)率分布，成像結(jié)果如圖3所示。

圖3 不同算法的電阻抗成像效果

由圖像重建方法及重建結(jié)果得到如下結(jié)論：

1）圖像的質(zhì)量及神經(jīng)網(wǎng)絡(luò)的泛化能力與輸入輸出的樣本對數(shù)有直接關(guān)系，樣本越多效果越好。

2）采用BP-PSO的EIT圖像重建算法，可離線充分訓(xùn)練，可使成像速度提高，其速度要優(yōu)于動態(tài)反投影重建算法及靜態(tài)成像算法。

3）在樣品區(qū)域中的不同位置改變電導(dǎo)率，該算法的成像效果要優(yōu)于反投影重建算法。

4）基于PSO優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的方法，較其它基于神經(jīng)網(wǎng)絡(luò)的EIT圖像重建方法收斂速度更快并且不易陷于局部極值。

[1]Cheney M.Electrical impedance tomography [J].S IAM Review，1999，41（1）：85-101．

[2]Bertrand M，Boulay C，Guardo R,et al.An experimental study in electrical impedance tomography using backprojection reconstruction.IEEE Trans Biomed Eng，1991；38（7）：617.

[3]Jan C de Munck，Theo J C Faes，Rob M Heethaar.The Boundary Element Method in the Forward and Inverse Problem of Electrical Impedance Tomography[J].IEEE Trans Biomed Eng 2000,47（6）：792-800.

[4]Webster J G（Ed）.Electrical Impedance Tomography.Bristol,England：Adam.Hilger,1990：1-205.

[5]SECRESTBR，LAMONT G B.Visualizing Particle Swarm optimization.In Proceedings of the 2003 IEEE Swarm Intelligence Symposium，SIS’03.Indianapolis（IN，USA）：2003.198-204.