基于MATLAB的一種并聯頂舉機構逆解與工作空間分析

姚榮華，陳品志，何鵬飛

YAO Rong-hua，CHEN Pin-zhi，HE Peng-fei

（北京理工大學 機械與車輛學院，北京 100081）

0 引言

在震后救援工作中，傳統的頂舉機械如千斤頂只能在單一方向上進行頂舉工作，一旦頂舉方向需要變化則千斤頂必須卸載后重新安裝頂舉，如果方向還有偏差，則須再次卸載以變換頂舉變向，這樣反復調整浪費了大量時間，嚴重限制了震后施救效率的提高。針對以上問題，本課題組設計了一種空間三自由度的頂舉救援機器，該頂舉機械在重載下可以實時調整頂舉姿態，改變項舉方向，從而大大提高頂舉工作的效率。

1 機構簡介

機構簡圖和工作樣機分別如圖1、圖2所示，該機構有三個空間自由度，靠三根雙作用液壓桿的伸縮控制整個機構的運動。空間并聯頂舉機構實現了空間狀態實時變換的功能，機構底部可適應各種不同的工作環境方便安裝。機構的上下平面的工作范圍均可調整，上平臺半徑r調節范圍200~290mm，下平臺半徑R為300~420mm，桿的長度為430~680mm，C1、C2、C3為底部平臺的三個固定點，A1、A2、A3為上平臺的三個球絞點，底部三個點與三根桿的連接使用銷釘連接只能繞銷釘的軸線方向進行旋轉。機構上的三根桿C1A1、C2A2、C3A3是三根液壓桿即該機構的三個自由度。

圖1 機構簡圖

圖2 工作樣機

液壓桿的行程是通過液壓系統一系列的電磁閥控制的。單片機中輸出的電信號通過調制解調，功率放大之后去控制電磁閥來調節液壓油的流量，最終實現對機構的電、液、機控制。然而在控制中最困難的就是根據想要上平面姿態去求三根桿的行程，這就需要單片機能夠根據實際所需姿態迅速反求出C1A1、C2A2、C3A3的長度，然后給出電信號進行控制。求三桿的長度要進行逆解分析，而控制中還要知道機構的運動空間，防止機構運動到空間的奇異點從而破壞機構。求機構的空間奇異點就要求出機構的空間運動包絡面，反求出桿長的伸縮范圍，這樣機構的控制就在理論上實現了。以下介紹了針對該機構控制的理論基礎和用MATLAB計算的方法。

2 機構逆解與工作空間分析

點C1、C2、C3在定坐標系O-XYZ下的絕對坐標，其中R1、R2、R3是機構底部三根連接桿的工作長度，z1、z2、z3為固定點的安裝高度。

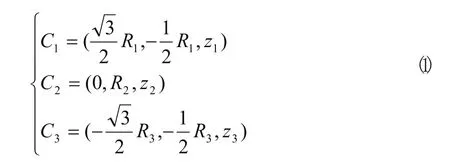
點A1、A2、A3在動坐標系P-X1Y1Z1下的相對坐標，其中r1、r2、r3為頂部三根桿的工作長度

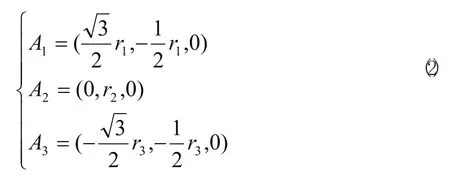
動坐標系P-X1Y1Z1對定坐標系O-XYZ的可用歐拉角表示的齊次坐標變換矩陣描述。用歐拉角描述機構空間姿態，由于歐拉角表示的旋轉矩陣只有三個參數，所以用歐拉角將平臺的位姿參數與變換矩陣聯系起來，方便了求解運算。

設上平面的單位矢量為Nt=（ntx,nty,ntz）T，歐拉角為α、β 、γ，運動平臺與絕對坐標系坐標軸的方向余弦角為θx、θy、θz。

為了計算方便以及保證 ntx、nty、ntz與 α、β、γ 為單值對應，需要對歐拉角做如下規定：

平臺的法向單位矢量即為方向余弦：

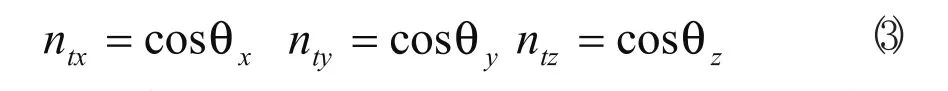
根據實際的運動情況，不能取負值，所以有

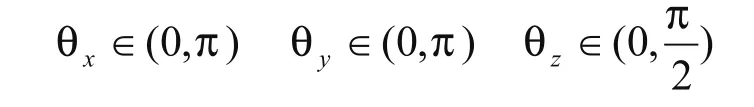
用歐拉角表示的平臺姿態的旋轉矩陣為：

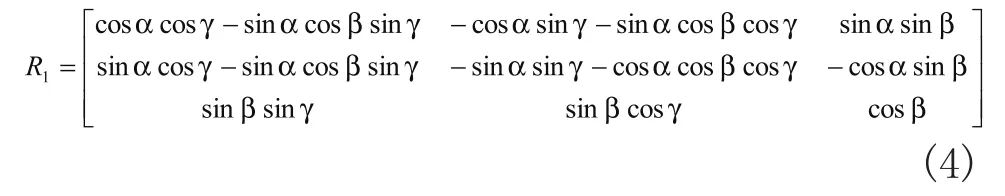
由于平臺的軸線與所定義的動坐標系的Z1軸重合，所以旋轉矩陣R1的最后一列正好是動坐標系軸的單位矢量，可以得到三個方程：

將平臺的空間姿態角通過上式轉化成為歐拉角的表示。

根據，兩個歐拉角可以由平臺的方向余弦角完全確定，歐拉角表示的動平臺姿態的旋轉矩陣的每一列分別表示動平臺坐標系軸對軸的方向余弦，于是有：

其中對應的元素相等，還有加上平臺不自轉的條件-α=γ：。在結合實際模型，還應有約束條件：

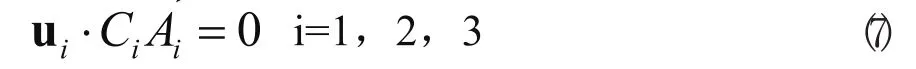
其中u1、u2、u3為三個轉動副的軸線的單位方向矢量，此外機構桿長也為約束條件。

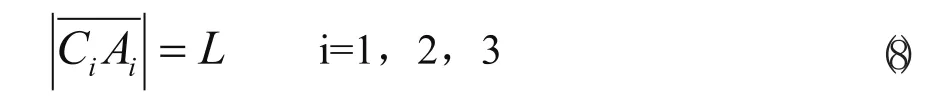
對于（7）式中的方程α、β 、γ為三個未知數，而θx、θy、θz為三個上平臺空間運動的姿態角為已知量，并且有cos2θx，cos2θy，cos2θz=1所以方程組（5）中只有兩個式子是獨立的，而θx、θy、θz中也只有兩個獨立的變量，在加上上平臺中心點的縱坐標，該機構的數學描述中只有三個獨立的變量，即該機構只有空間的三個自由度。

對實際機構模擬還應加上頂部運動平臺球角運動角度的約束條件，是通過運動桿的單位矢量與平臺三定點與中心形成的向量的夾角確定，限定范圍為30度。

3 基于MATLAB的逆解與工作空間仿真

在MATLAB中要先對機構進行描述，用MATLAB的程序語言描述運動平面內的三點在動坐標系中的位置和底部三點在定坐標系中的位置，然后利用動坐標系相對于定坐標系的坐標變換矩陣將描述機構的所有的點均轉換到一個統一的坐標系中研究。

在計算機仿真中利用數值計算的方法非常利于簡化程序而且運算簡單。根據平臺的最終空間要達到的空間姿態去反求其他各點的位置和桿的長度。這里通過循環語句對機構的各種空間姿態進行取值和密化，由于機構為空間三自由度，所以只要對其中的三個變量進行循環自動賦值就可以取到機構所能達到的空間姿態。

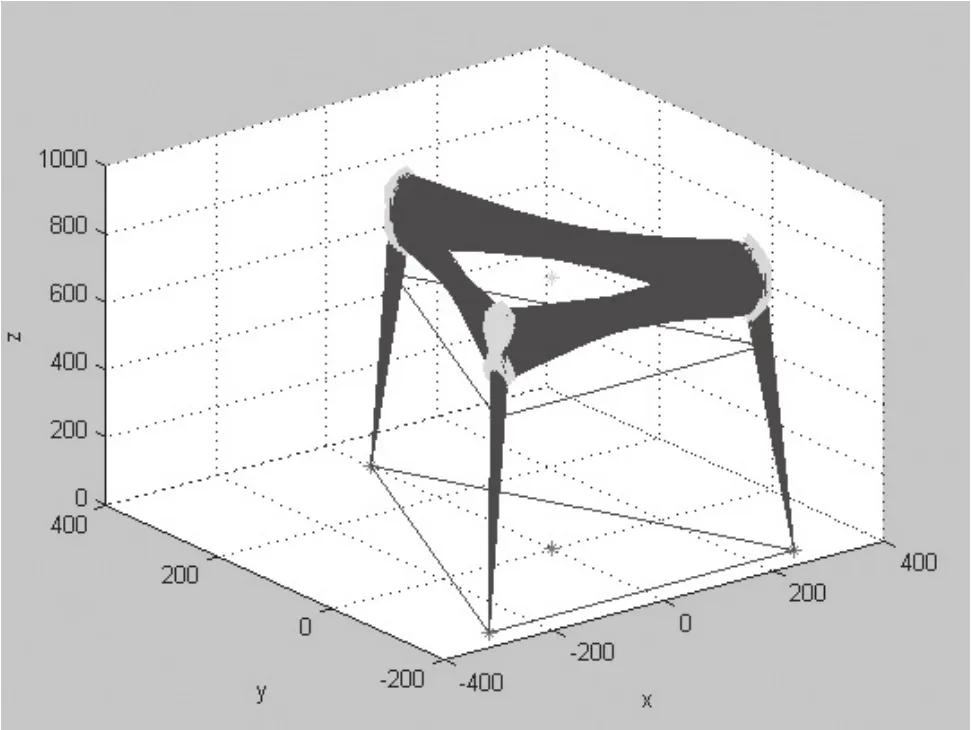
圖3 機構的逆解分析

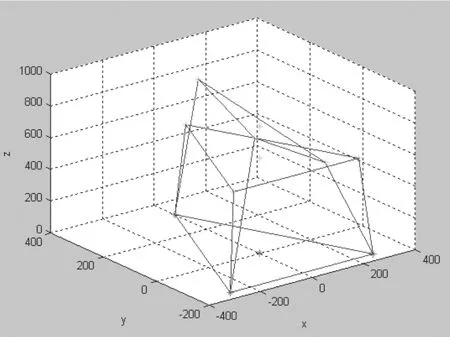
圖4 機構的工作空間分析

進行空間機構仿真時，對于機構在實際運動中存在的約束是通過對空間中已求出的理想點進行再次分析模擬的。用理想模型中的出的機構空間點進行桿長和向量空間夾角的描述，通過如桿長和夾角再對這些理想點進行篩選，最終就可以得到機構的實際運動空間。

在程序中進行自動取值去掉而輸入自定的歐拉角（根據平臺姿態用公式得出），則可計算出該姿態下的平臺動桿所應達到的桿長。對所取的空間姿態向量越密集，則對平臺的空間姿態描述越精確。圖3為在已知上平面的θx、θy、Z的條件計算出桿長繪制的圖，由于沒有加球絞限制和桿長限制，所以達到的空間旋轉范圍大，是對逆解分析算法的一種驗證。圖4是加上限制條件之后在空間某一固定高度繪制出的機構空間工作范圍，可以看到機構在固定高度上的旋轉空間范圍是比較有限的，這主要是在設置球絞工作范圍時的取值較小，在實際產品中使用的直線桿端球軸承的工作范圍是30度，若要增大產品的工作范圍就必須定做球絞角度更大的軸承。通過工作空間分析知道了機構的空間工作范圍，提供了進行控制的桿長參數，確定了三桿聯動在達到預期位置過程中桿長的變化范圍與最終確定值。

4 對比分析

實際試驗發現機構在某一運動高度時，其旋轉空間的范圍不是很大，三根桿長的伸縮范圍受頂部球絞的旋轉角度制約嚴重，從而造成三根桿的長度差并不是很大即上平臺的空間旋轉范圍較小。但由于機構垂直方向上的運動不受球絞的制約且伸縮范圍大，機構在整個空間的運動范圍能夠滿足設計之初多方向頂舉的要求，并且在實際試驗時，由于機械零件的公差的存在使機構運動并不嚴格按照計算時的約束進行運動，運動范圍稍大于計算得到的范圍。

[1]韓建有.高等機構學[M].北京：機械工業出版社,2004．

[2]劉峰,陳文凱.3自由度并聯機器人的研究現狀和發展前景[J].企業技術開發,2006,（1）.