三自由度繩驅動并聯機器人運動學分析

喬文剛，盛如龍，喬 魏

QIAO Wen-gang，SHENG Ru-long，QIAO Wei

（內蒙古科技大學 機械工程學院，包頭 014010）

0 引言

自1987年Hunt提出并聯機器人結構模型以來，并聯機器人的研究受到廣泛的關注，并取得了一定的成果。與串聯機器人相比并聯機器人的工作空間較小；并聯機構的靈活性較差，且在工作空間內部存在著奇異點；其控制系統非常復雜，致使研究難度、生產成本等相應增加。并聯機器人由于其運動速度高、動態響應快、定位準確性好等優點，在某些領域作為串聯機器人強有力的補充，所以應用潛力非常大，廣泛應用于裝配、包裝、點焊等領域。近年來，少自由度并聯機構在工業一線應用成為機器人技術研究的新領域。與六自由度Stewart平臺相比，少自由度機構具有結構簡單，造價低等特點，因此在工業生產及其它領域具有廣闊的應用前景。

本文提出一種三自由度繩驅動并聯機器人，其驅動器可以直接安裝在底座上，不需桿作支撐，因此結構簡單、實用性強、慣性小、具有重調整和可移動性強、完全分離的傳動優點。

1 繩驅動并聯機器人組成及工作原理

1.1 機構組成及特點

繩驅動并聯機器人（如圖1所示）是一種特殊的并聯機器人，由Stewar平臺發展而來。應為Stewar 平臺考慮腿部的質量影響，使得計算量和控制都非常復雜，而且不宜實現高速運動。繩作為柔性物質，只具有單向力，即只能承受拉力，這是繩驅動并聯機器人需要解決的問題，即要使

機器人在其工作空間內繩處處長緊。

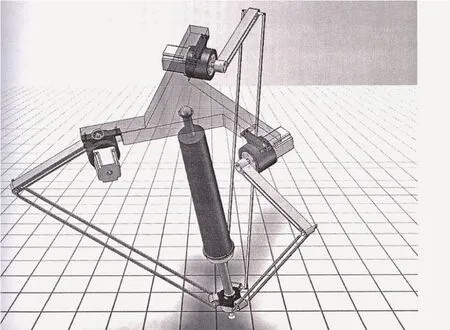
圖1 三自由度繩驅動并聯機器人

繩驅動并聯機器人有許多優點，包括：

1）大個子空間：一個絞盤可以提供很大的范圍的可變繩長。這樣的便利是其他機器人所不具備的。

2）低慣性：材料提供最高的力/質量比。當它們處于張緊狀態時，繩子只能緊，最大化了材料的力，因此，減小了控制器的質量和慣性。

3）結構簡單：繩簡化了控制器的機構，繩的柔性簡化了關節的連接及潤滑。

4）重調整和可移動性：絞盤可以簡單的拆卸來重調整，并且可以改變繩驅動控制器的工作空間。

5）完全分離的傳動：用全繩驅動控制器，所有的傳動和敏感部分可以放在離終端執行器和工作地帶很遠的地方。可適應危險的工作環境。

1.2 動作原理

三自由度繩驅動并聯機器人共計九個關節，包括三個轉動關節（即電機與擺桿的連接）和有六個球面副關節（即繩與擺桿機、動平臺的連接和氣缸與上下平臺的連接）。由于氣缸的兩端分別安裝在兩平臺的幾何中心，所以起輔助支撐作用不參與機構主要運動。該機構的動力源來自安裝在基座上的伺服電機，每個電機驅動一組擺桿和繩，繩的另一端與動平臺相連。通過伺服電機輸出的一定的轉角帶動擺桿使其擺動帶動繩，從而使動平臺實現預期的運動。由于繩只能承受張力所以在上下平臺之間安裝一氣缸來使繩時刻處于張緊狀態，同時利用氣缸來作一支撐，使機構具有一定的剛度。

2 運動學分析

2.1 坐標系建立

1）XYZ：固聯于基座的質心O點，并且處于三個驅動器軸垂分線的交點。

2）XiYiZi：固聯于第i個驅動器上，其中Xi垂直于轉軸i并且通過基座質心點O。Yi沿著轉軸i，Zi根據右手笛卡爾坐標系確定。

如圖2所示，三自由度繩驅動并聯機器人坐標系的建立。

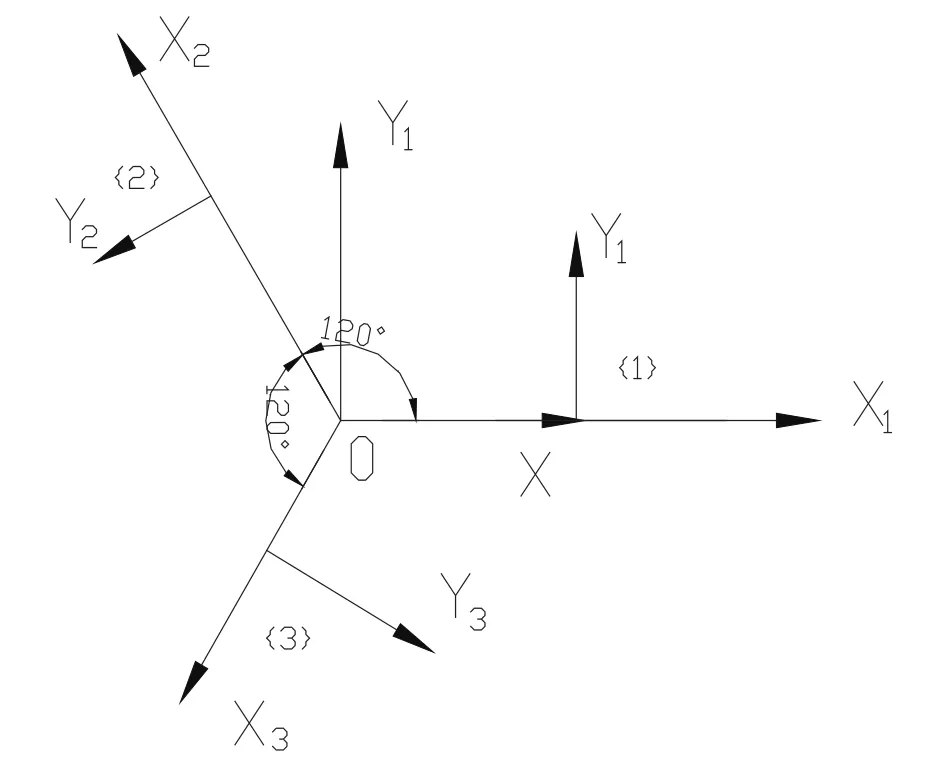
圖2 三自由度繩驅動并聯機器人坐標系

2.2 變量和向量

1）P：移動平臺的質心

3）Ai：第i軸在XiZi平面投影

4）Bi：擺桿末端在XiZi平面投影

5）Ci：移動平臺末端在XiZi平面的投影

6）?i：X與Xi的夾角

7）θ1i： Xi與的夾角

8）θ2i：繩與Xi的夾角

9）θ3i：繩與Yi的夾角

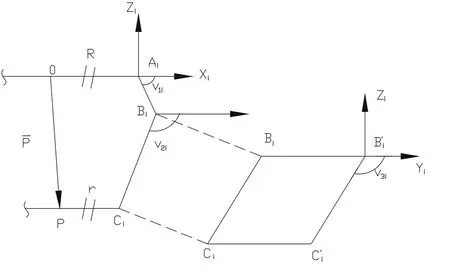
圖3 三自由度繩驅動并聯機器人第[i]坐標系

2.3 逆向運動學分析

逆向運動學是用來解決移動平臺在笛卡爾坐標系已知的情況下來求解三組驅動器的角度。在計算中移動平臺的位置由 給出。逆向運動學通過計算得到三個關節空間的變量θ1i、θ2i和θ3i，這樣就可以確定機器人的可能的形位。

同樣

因此對于給定的移動平臺的位置參數，可以得到4組解。

2.4 前向運動學分析

前向運動學主要用來解決對于已知關節空間角度輸入相對應的移動平臺的笛卡爾坐標，對于這個機器人來說，已知關節輸入是繩長對應的移動平臺輸出是P在XYZ坐標系下的坐標值。

給定θ1i為已知，可以導出9個未知數的9組方程，即：

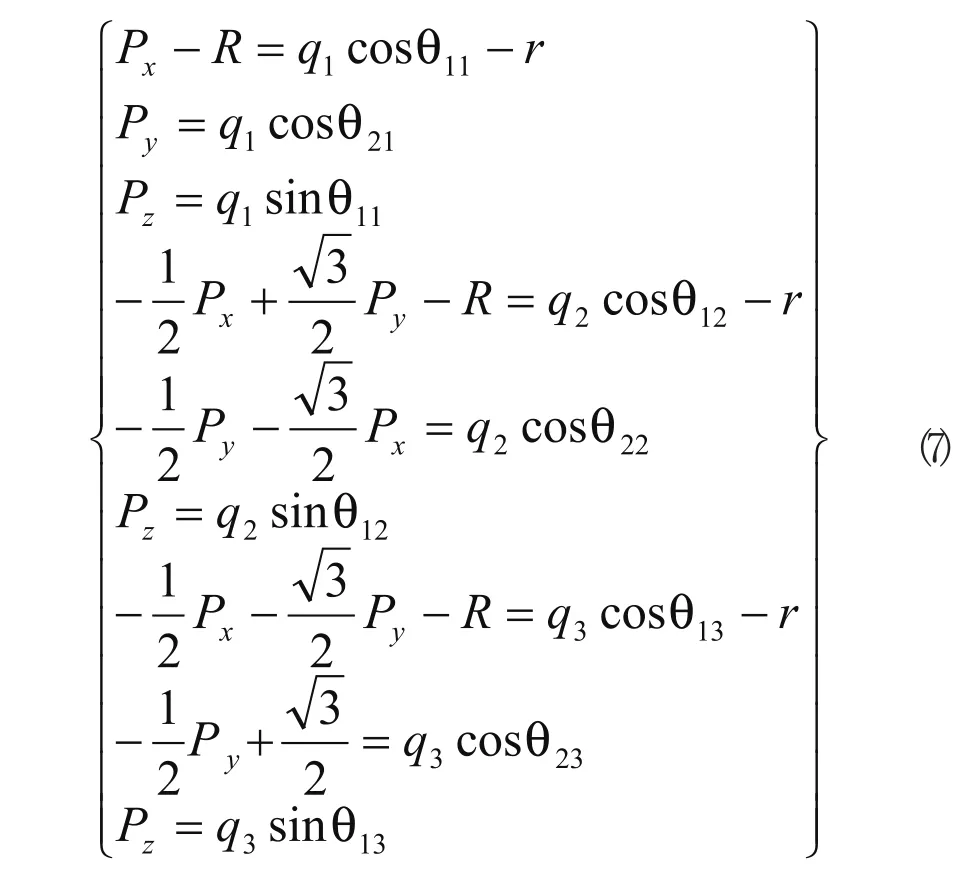
通過消元法可以得到只含有pxpypz的三個方程，即：

其中：

2.5 數值分析

由設計模型可知：R=300mm，r=80mm，l=468mm，L=277mm。利用MATLAB軟件進行計算，角度輸入值如表1所示。

表1 角度輸入

在求正解過程當中，計算的結果（位置輸出）為x、y、z，其由兩組解構成，則動平臺有八種可能的位置，通過模型及機構坐標系進行分析，采用排除法得到動平臺正確的位置輸出，如表2 所示。

表2 動平臺位置輸出

經過MATLAB的計算可知，正解與反解的結果是一一對應，故關于位置正解與位置反解推導過程是正確的。

3 結束語

本文在闡述三自由度繩驅動并聯機器人結構特點的基礎上，對其運動學進行了分析，得出了該機器人運動學正反解方程，為該機器人進一步的研究奠定了基礎。從運動學方程顯而意見，該機構具有正反運動學計算相對簡單、易得出顯示表達式、易于實現實時控制的特點，為以后該類機器人的應用推廣提供了可靠的理論依據。

[1]張春林,余躍慶,高等機構學[M].北京：北京理工大學,2005.

[2]馬香風.機器人機構學[M].北京：機械工業出版社,1991.

[3]宗光華.程君實,等.機器人技術手冊.北京：科學出版社，2007.

[4]劉雄偉,鄭亞青.6自由度繩牽引并聯機構的運動學分析[J].機械工程學報,2002,（38）：16-20.

[5]黃真.空間機構學[M].北京：機械工業出版社,1991.

[6]熊有倫.機器人學[M].北京：機械工業出版社,1996.

[7]梁崇高,榮輝.一種Stewart平臺型機械手位移正解[J].機械工程學報,1991,27（2）：26-30.

[8]趙杰,朱延河,蔡鶴皋.Delta型并聯機器人運動學正解幾何解法[J].哈爾濱工業大學學報,2003,35（l）：25-27.