函數(shù)漸進(jìn)界的性質(zhì)研究

楊冀林

YANG Ji-lin

（赤峰學(xué)院 計(jì)算機(jī)科學(xué)與技術(shù)系，赤峰 024000）

1 函數(shù)漸進(jìn)界的定義

定義1：設(shè)f（n），g（n）是定義在自然數(shù)集N上的兩個(gè)非負(fù)實(shí)值函數(shù)，如果存在自然數(shù)n0和正常數(shù)c，使得?n≥n0，都有f（n）≤cg（n），則稱g（n）是f（n）的一個(gè)漸進(jìn)上界，記作f（n）=O（g（n））。

圖1 漸近上界的幾何解釋

定義2：設(shè)f（n），g（n）是定義在自然數(shù)集N上的兩個(gè)非負(fù)實(shí)值函數(shù)，如果存在自然數(shù)n0和正常數(shù)c，使得?n≥n0，都有f（n）≤cg（n），則稱g（n）是f（n）的一個(gè)漸進(jìn)下界，記作f（n）=O（g（n））。

圖2 漸近下界的幾何解釋

定義3：設(shè)f（n），g（n）是定義在自然數(shù)集N上的兩個(gè)非負(fù)實(shí)值函數(shù)，如果存在自然數(shù)n0和兩個(gè)正常數(shù)c1，c2使得?n≥n0，都有c1g（n）≤f（n）≤c2g（n），則稱g（n）是f（n）的緊致的界，記作f（n）=Θ（g（n））。

由定義可知f（n）=Θ（g（n）），當(dāng)且僅當(dāng)g（n）= Θ（f（n））。

定義4：設(shè)f（n），g（n）是定義在自然數(shù)集N上的兩個(gè)非負(fù)實(shí)值函數(shù)，如果對(duì)每一個(gè)常數(shù)c＞0，都存在自然數(shù)n0，使得?n≥n0，都有f（n）＜cg（n）則g（n）稱是f（n）的一個(gè)上界，記作f（n）=o（g（n））。

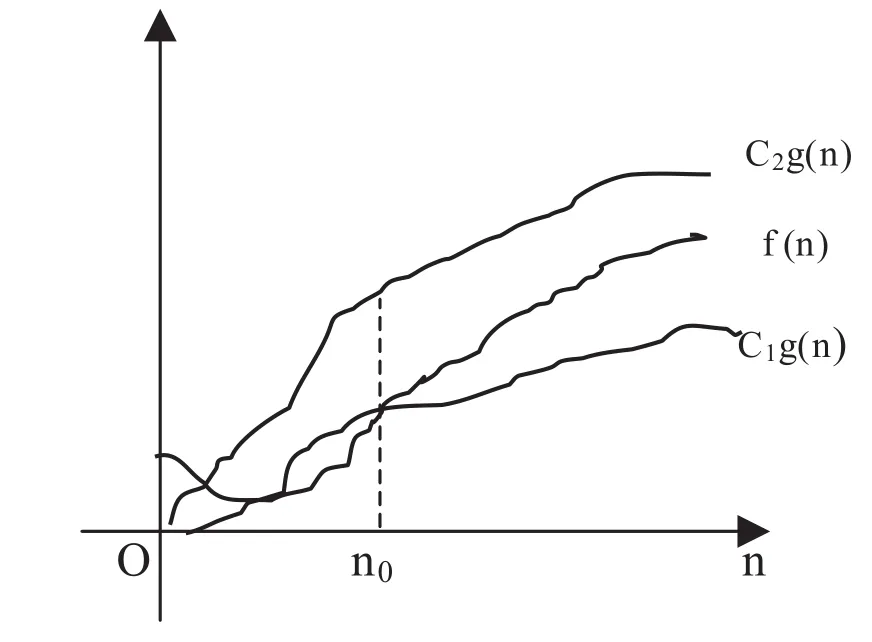
圖3 緊致界的幾何解釋

2 函數(shù)漸進(jìn)界的性質(zhì)

定理1 f（n）=Θ（g（n）） iff f（n）=O（g（n））且f（n）=Ω（g（n））。

證明?，若f（n）=Θ（g（n）），則根據(jù)定義3，存在自然數(shù)n0和正常數(shù)c1和c2，

使得當(dāng)n≥n0時(shí)有c1g（n）≤f（n）≤c2g（n）。

由上式右邊不等式可得f（n）=O（g（n））

由上式左邊不等式可得f（n）=Ω（g（n））

?，若f（n）=O（g（n））且f（n）=Ω（g（n））

根據(jù)定義1，存在自然數(shù)n1和正常數(shù)c1，當(dāng)n≥n1，有f（n）≤c1g（n） （1）

根據(jù)定義2，存在自然數(shù)n2和正常數(shù)c2，當(dāng)n≥n2，有f（n）≤c2g（n） （2）

取n0=max{n1，n2}當(dāng)n≥n0時(shí)，由（1）（2）式有c1g（n）≤f（n）≤c2g（n）

所以有f（n）=Θ（g（n））。

定理2 符號(hào)Ο，Ω，Θ，ο具有傳遞性，即有以下等式成立：

1）若f（n）=O（g（n）），且g（n）=O（h（n）），則f（n）= O（h（n））

2）若f（n）=Ω（g（n）），且g（n）=Ω（h（n）），則f（n）= Ω（h（n））

3）若f（n）=Θ（g（n）），且g（n）=Θ（h（n）），則f（n）= Θ（h（n））

4）若f（n）=o（g（n）），且g（n）=o（h（n）），則f（n）= o（h（n））

以上四個(gè)結(jié)論的證明是類似的，現(xiàn)只證明結(jié)論1）

4.在年終考核時(shí)，考核政策應(yīng)當(dāng)向生活教師適度傾斜。原因在于，學(xué)校以教學(xué)為主，作為負(fù)責(zé)學(xué)生安全和后勤工作的生活教師往往會(huì)受到忽視，其工作上的辛勤付出往往無(wú)法得到與之匹配的重視和關(guān)照，影響其工作積極性。而通過(guò)適度的考核政策傾斜，能夠讓生活教師充滿干勁，以更為飽滿的工作熱情投入到其本職工作之中。

證明1）若f（n）=O（g（n）），且g（n）=O（h（n）），則由定義1知，存在自然數(shù)n1和正常數(shù)c1，當(dāng)n≥n1時(shí)，有f（n）≤ c1g（n），同時(shí)存在自然數(shù)n2和正常數(shù)c2，當(dāng)n≥n2時(shí)，有g(shù)（n）≤c2h（n），取n0=max{n1，n2}，當(dāng)n≥n0時(shí)，有f（n）≤c1g（n） ≤c1c2h（n）=c · h（n）（c=c1c2）

根據(jù)定義1有f（n）=O（h（n））。

定理3：設(shè)f（n），g（n）是定義在自然數(shù)集N上的兩個(gè)非負(fù)實(shí)值函數(shù)，則有以下結(jié)論：

于是，根據(jù)定義定義3有f（n）=Θ（h（n））。

定理4：設(shè)f（n），g（n）是定義在自然數(shù)集N上的兩個(gè)非負(fù)實(shí)值函數(shù)，若對(duì)于某個(gè)其它的非負(fù)實(shí)值函數(shù)h（n）有f（n）=O（h（n）），g（n）=O（h（n）），則有f（n）+g（n）=O（h（n））。

證明：由于f（n）=O（h（n）），所以存在自然數(shù)n1和正常數(shù)c1，當(dāng)n≥n1時(shí)，有f（n）≤c1h（n）

同理由于g（n）=O（h（n）），所以存在自然數(shù)n2和正常數(shù)c2，當(dāng)n≥n2時(shí)，有f（n）≤c2h（n）取n0=max{n1，n2}當(dāng)n=n0時(shí)，由以上二式有：f（n）+g（n）≤（c1+c2）h（n）=c·h（n）（c=c1+c2），所以有f（n）+g（n）=O（h（n））。

則有f（n）+g（n）=Θ（f（n））。

定理5：設(shè)f（n），g（n）是定義在自然數(shù)集N上的兩個(gè)非負(fù)實(shí)值函數(shù)，則有：

max{f（n），g（n）}=Θ（f（n）+g（n））。

證明：不妨假設(shè)max{f（n），g（n）} =f（n），于是g（n）≤f（n），所以 f（n）+g（n）≤2f（n）

另一方面由于f（n），g（n）的非負(fù)性，顯然有f（n）≤f（n）+ g（n）

從而有f（n）=O（f（n）+g（n）），即有

由（1）（2）式得到max{f（n），g（n）}=Θ（f（n）+g（n））。

1）若 ，則p（n）=O（nk）

2）若 ，則p（n）=Ω（nk）

3）若 ，則p（n）=Θ（nk）

結(jié)論1）2）的證明類似，僅證結(jié)論1）和3）。

此外，函數(shù)漸進(jìn)的界還有一些算法中常用的性質(zhì)，限于篇幅列出不予證明：

1）任何常函數(shù)都是Ο（1），Ω（1），Θ（1）

2）Ο（cf）=Ο（f），Ω（cf）=Ω（f），Θ（cf）=Θ（f），其中是c正常數(shù)。

3）Ο（f ·g）=Ο（f）·Ο（g），Ω（f ·g）=Ω（f）·Ω（g），Θ（f ·g）=Θ（f）·Θ（g），

3 結(jié)論

函數(shù)漸進(jìn)的界有許多重要性質(zhì)，本文給出函數(shù)漸進(jìn)界的概念及幾何解釋，Ο，Ω，Θ，ο符號(hào)及其等價(jià)性，分類歸納出算法分析中常用的一些性質(zhì)，并利用極限理論給予嚴(yán)格的數(shù)學(xué)證明，這無(wú)疑將對(duì)系統(tǒng)掌握函數(shù)漸進(jìn)界的性質(zhì)，提高算法復(fù)雜度的分析能力提供有益的幫助。

[1]霍衛(wèi)紅,算法設(shè)計(jì)與分析[M].西安電子科技大學(xué)出版社，2005：8-11.

[2]Jon Kleiberg,Eva Tardos,算法設(shè)計(jì)[M].清華大學(xué)出版社,2007：25-30.

[3]M.H.Alsuwaiyel,算法設(shè)計(jì)技巧分析[M].電子工業(yè)出版社,2009：11-20.

[4]屈婉玲,算法分析與計(jì)算復(fù)雜性理論講義,2010：27-31.

[5]盧開澄,計(jì)算機(jī)算法導(dǎo)論[M].清華大學(xué)出版社,1996：9-10.

[6]王曉東,計(jì)算機(jī)算法設(shè)計(jì)與分析[M].電子工業(yè)出版社，2004：1-5.

[7]宋文,杜亞軍,算法設(shè)計(jì)與分析[M].重慶大學(xué)出版社：2004：5-7.