一種改進的PSO網格調度算法

楊長興，胡 金

（中南大學 信息科學與工程學院，湖南 長沙410083）

在網格計算中，任務管理、任務調度和資源管理是網格的3個基本功能。任務調度是網格系統的一個關鍵問題，關系到網格能否高效利用資源、快速完成任務以及實現系統負載均衡。同時它也是一個NP完全問題[1]，即得到一個最優的調度方案或是在有限的時間里找出最優(任務,資源)的匹配方案是不可能的。目前多采用啟發式算法解決此類問題。

近年來，很多學者將啟發式算法應用于任務調度中，并取得了較好的研究成果[2-5]。其中，GA算法可能找到最優解，但選擇過程存在隨機性，不能確保得到最優解，同時開銷大，運行時間長；AA算法雖然有正反饋機制能避免早熟現象，但容易收斂于局部最優，而且算法復雜，搜索時間長；SA算法能以一定的概率接受差的解而可能跳出局部極小，是一種全局最優算法，但是搜索時間比較長；PSO粒子群優化算法[6]搜索速度快、操作簡單、效率高，但是易陷入局部極值，搜索精度不高。

針對PSO易早熟、求解質量不高的問題，為實現最小化任務完成總時間(makespan)，本文提出一種基于獨立任務調度的改進PSO網格調度算法MCPSO(An improved PSO of grid scheduling algorithm under the meta task)。該算法的主要思想是：首先采用混沌[7]序列初始化粒子的位置，并在產生的大量粒子中擇優選出初始種群；然后在粒子更新時引入混沌搜索，隨機產生若干混沌序列并把最優混沌序列得到的位置和當前粒子最優位置比較，如果優于當前粒子，則更新當前粒子的最優位置，引導當前粒子跳出局部最優點，快速尋找最優解。實驗表明，該算法改善了PSO算法易陷入局部最優問題，同時兼顧更好的makespan和負載均衡，有效提高網格的性能。

1 問題定義

圖1所示是一個簡單的任務調度流程圖，其中MDS(Monitoring and Discovering Service)是資源監控與發現服務，用于收集和發布系統狀態信息。

如圖1所示，首先任務劃分模塊將應用程序劃分為若干個子任務，然后調度模塊從網格資源中的信息采集模塊MDS收集必要信息，最后按一定的策略對任務進行分發。

通常在網格環境下主要考慮一組相互獨立、任務之間沒有數據和通信依賴的獨立任務(metatask)。目前多數研究是基于此展開的。本文將主要研究獨立任務調度。

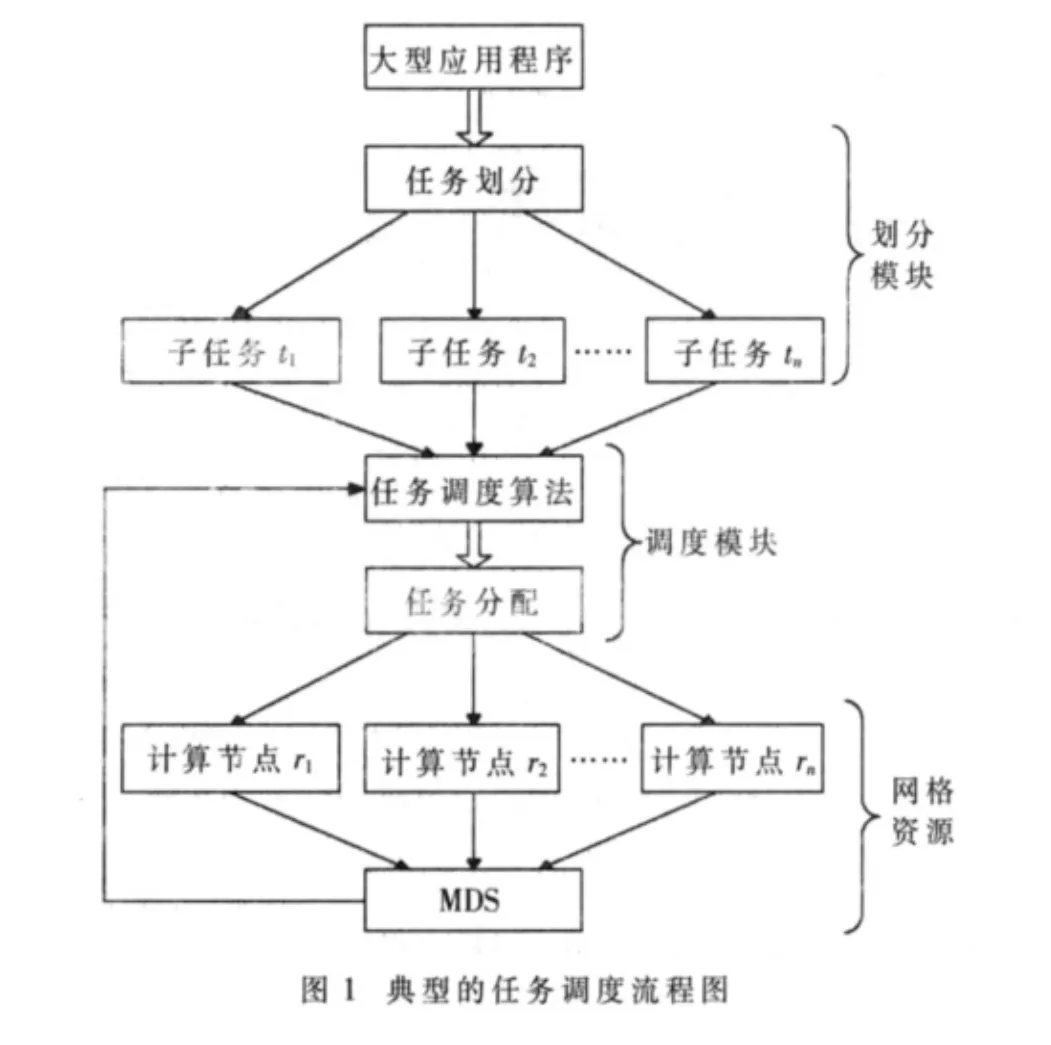
現假定虛擬組織VO中用戶提交了若干個任務，這些任務經由圖1中的劃分模塊分成n個獨立子任務t1、t2、…、tn組成子任務集合 T，網格系統中有 m個節點(網格資源)r1、r2、…、rm構成資源集合R。任一任務 ti可以在任一節點rj上執行，rj在同一時刻只能處理一個任務，而 ti不能同時在兩個節點上執行，ti一旦開始，rj被獨占，直到ti完成后才能執行其他任務。用一個n維向量(w1，w2，…，wn)表示任務的預計完成時間，其中 wi為任務i的預計完成時間。

定義1(任務映射集)n個任務映射到m個節點的映射方案T→R集合即任務映射集MAP。集合MAP={map1，map2，…，mapn}，其中 mapi表示第 i個任務在映射到的節點mapi上執行。

定義2(節點工作時間)節點工作時間RCj是指節點j處理完所有分配給它的任務所花費的時間。如式(1)所示：

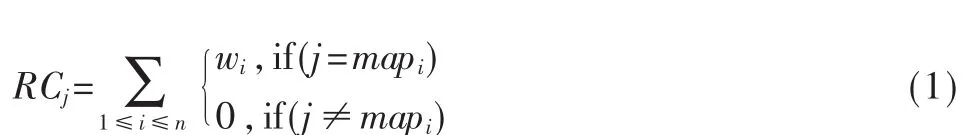
定義 3(時間跨度)時間跨度即 makespan，是指任務集合T中第一個任務開始執行到最后一個任務完成的時間。在某調度算法下的makespan也稱為該算法的調度長度，makespan越小，調度策略越好。最優跨度ω為網格當前實際跨度的最好值，最優調度的下界是將任務平均分到各個計算資源上，此時得到的ω值為理論最優跨度ωmin即均衡負載。

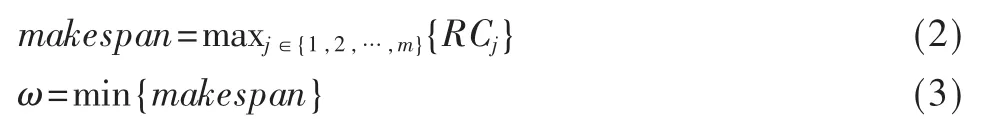
定義4(負載均衡度)計算資源上的任務稱為負載。當計算資源上的負載超過ωmin時該計算資源為重載資源，而當負載低于ωmin時為輕載資源。任務調度的目標是最小化資源上的負載，使得各個資源負載基本相同，這個過程也稱為負載均衡。負載均衡度β按式(5)計算，表示計算資源負載偏離均衡負載ωmin的程度，其數值越小，網格系統就越均衡。

獨立任務調度的數學模型為：

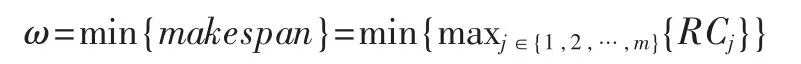
2 改進PSO的網格調度算法

2.1 標準PSO算法

粒子群優化算法PSO(Particle Swarm Optimization)是由Eberhart和Kennedy于1995年發明的一種全局迭代優化算法。PSO先生成初始種群，即在可行解空間中隨機初始化一群粒子，每個粒子代表著優化問題的一個潛在可行解。每個粒子將在解空間中“飛行”，并由一個速度決定其方向和距離。通常粒子將追隨當前的最優粒子而動，并經過多次迭代得到最優解。在每一次迭代時，粒子將跟蹤兩個極值，一為粒子本身迄今找到的最優解pbest，另一個為全種群迄今找到的最優解gbest。

每一代粒子速度和位置更新公式如下：

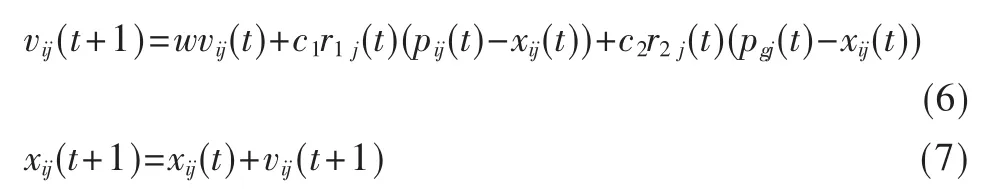
式中，vij(t)、vij(t+1)表示第 i個粒子在第 j維方向上的當前速度和更新后的速度；xij(t)、xij(t+1)表示第i個粒子在第j維方向上的當前位置和更新后的位置；w為慣性因子，作用是控制和提高優化效率；c1、c2為學習因子，通常在 0～2 間取值；r1～U(0，1)，r2～U(0，1)為兩個相互獨立的隨機函數；pij(t)表示第i個粒子經歷過的最好位置矢量即個體最好位置在第j維方向上的位置；pgj(t)表示群體中所有粒子經歷過的最好位置矢量即全局最好位置在第j維方向上的位置。

2.2 混沌優化

由確定的運動方程得到的具有隨機性的運動狀態稱為混沌運動。混沌是自然界中一種常見現象，其變化過程看似雜亂無章，但不是完全混亂，而是有一定的規律性。將方程中呈混沌狀態的變量稱為混沌變量，混沌變量對初值十分敏感。混沌變量具有從任意點(除不動點)出發，按確定公式遍歷所有狀態的特點，即確定性、遍歷性，表現形式如同隨機變量。一個典型的混沌系統是Logistic方程，其表達式為：式中，μ 為控制參數，0≤μ≤4；un∈[0，1]。

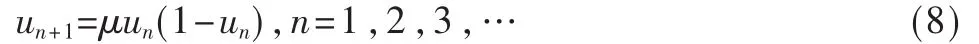
混沌搜索的主要思想是通過混沌系統如式(7)產生混沌序列，然后通過載波的方式

將其映射到優化空間中，也就是將混沌變量的值域“放大”到優化變量的取值范圍內。

2.3 改進PSO的網格調度算法(MCPSO)

PSO具有很強的全局搜索能力，但不能保證全局收斂。當粒子自身信息和個體極值信息占優時，往往停滯于局部最優解，且隨機初始化的種群質量不高，甚至距離最優解位置較遠。而混沌具有良好的遍歷性、隨機性以及一定的突跳能力，易跳出局部極值點，最終可能得到最優解。

因而可以利用混沌的遍歷性，在初始化時產生大量粒子，從中擇優選出初始種群。同時在粒子位置和速度更新時，引入混沌搜索，并把最優混沌序列得到的位置與當前粒子最優位置相比較，如果優于當前粒子則進行替換。這樣可以有效減少算法收斂于局部極值的現象。算法流程如下：

(1)給定種群大小 POPSIZE、最大迭代次數、慣性權值 w、學習因子 c1、c2及控制參數 μ等。

(2)混沌初始化：

①隨機產生一個n維每個分量數值在[0，1]上的向量，z1=(z11，z12，…，z1n)，n 為種群的大小，根據式(8)，得 n個混沌序列 z1，z2，…，zn。

②利用式(9)將 zi，1≤i≤n分量載波到相應的變量取值區間，選出較優的POPSIZE個粒子作為初始種群。

(3)隨機初始化各個粒子的初始速度并計算其適應值，設置各個粒子的初始極值并計算種群極值。

(4)根據式(6)、式(7)更新粒子位置和速度。

(5)啟動混沌搜索。隨機產生d個[0，1]上的隨機數，根據式(8)得到d個混沌序列，并把產生的混沌序列依次載波放大到對應變量的取值范圍上，從中選出最優位置。

(7)更新個體極值和群體極值。

(8)跳至步驟(4)直到算法到達最大迭代次數。

(9)輸出全局最優值和全局最優粒子、最優跨度ω、負載平衡度β。

2.4 問題編碼

對于n個任務m個資源的調度，粒子的位置和速度均用n維向量表示，維數和任務數一致。如位置向量(x1，x2，…，xm)中第 i維分量 xi表示任務 ti的權值，是[0，m)之間的一個隨機數。當n=10，m=5時，各個節點對應的權值范圍如表1。

表1 權值與節點序號對應表

若某粒子的位置矢量表示如下：

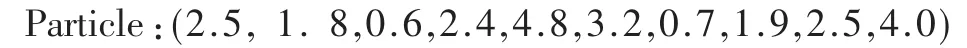
上述粒子即為任務的一個調度方案，由表1可得任務與節點的映射關系如表2所示。

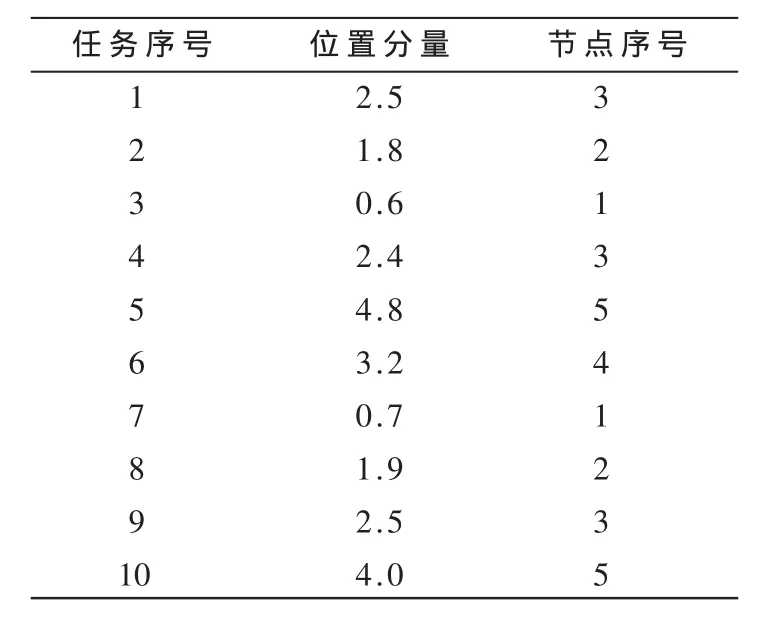
表2 基于節點編碼的任務分配方案

3 實驗與性能分析

以GridSim工具包為基礎構建網格仿真環境，將本文提出的MCPSO算法與基于獨立任務的基本粒子群優化算法MPSO算法進行對比分析。

PSO算法參數設置如下：種群大小POPSIZE=10，學習因子c1=c2=2.05，慣性因子ω=0.729，算法最大迭代次數為 1 000，混沌控制參數 μ=4。測試運行 50次，取 50次實驗的平均結果作為實驗結果。

實驗中有5個節點，10個任務，各個任務的預計完成時間{10,42,34,27,56,79,77,62,81,51}，單位為 s。

實驗從調度方案的求解質量、makespan、負載平衡度3個方面比較兩種算法的性能。

求解質量如表3所示。

表3 實驗結果比較

比較可知，本文提出的MCPSO算法比MPSO有更好的性能，平均跨度值與最好解的偏差小，最好解的次數明顯多于MPSO算法，最差解也明顯優于MPSO，MCPSO算法的求解質量更好。

為了觀察算法的收斂特性，給出了兩種算法1 000次迭代的makespan變化曲線，如圖2所示。從圖2可以看出，MCPSO算法收斂速度優于MPSO算法的情況，并能得到更好的解，而且改進的PSO算法初始解明顯更優。

由圖3可知，兩種算法的負載均衡度隨著迭代次數的增加而減少，即負載均衡性能都有提升。而MCPSO算法的負載均衡性能大大好于MPSO算法。

通過實驗可以看出，基本粒子群能快速地找到較優解，但是后期逐漸收斂于該解，并處于“停滯”狀態，很難得到更優解。引入混沌機制的MCPSO算法，擁有基本粒子群算法快速收斂的特性，同時在未得到最優解的情況下，逐漸向最優解靠近，不斷得到更優解甚至最優解。

為改善網格調度性能，本文提出了基于獨立任務的改進PSO任務調度算法。該算法以時間跨度makespan為數學模型，結合粒子群算法和混沌優化原理，首先通過混沌初始化得到較優的初始種群，有效減少粒子飛向較優點的迭代次數；在更新粒子位置和速度時，對粒子的最優位置進行混沌搜索，試圖找出更優的位置，使粒子飛向更優位置而避免陷入局部最優位置。實驗表明，與基本粒子群算法MPSO相比，MCPSO算法能有效提升任務調度問題的求解質量，縮短了makespan，優化了計算節點的負載均衡性能。下一步的研究工作是在關聯任務調度時，如何利用該算法有效提高任務調度的效率，以及如何讓算法在當網格系統中用戶的實際需求多樣化時仍然有效。

[1]Dong Fangpeng,SELIM G.Scheduling algorithms for grid computing:state of the art and open problems[D].Technical Report.School of computing,Queen′s University.Kingston,Ontario,January,2006.

[2]賀曉雨.一種用于任務調度的廣義遺傳算法[J].計算機工程,2010,36(17):184-186.

[3]AGHDAM H,PAYVAR S.A Modified simulated annealing algorithm for static task scheduling in grid computing[C].International Conference on Computer Science and Information Technology，2008:623-627.

[4]Zhang Lei,Chen Yuehui,Yang Bo.Task scheduling based on PSO algorithm in computational grid[M].Intelligent System Design and Applications，2006.

[5]魏東，吳良杰，佐丹，等.基于混合蟻群算法的網格任務調度[J].計算機工程,2010,36(3):215-217.

[6]KENNEDY J,EBERHART R.Particle Swarm Op-timization[C].In proc.IEEE Int Conf on Neural Networks.Perth,1995.

[7]李兵,蔣慰孫.混沌優化方法及其應用[J].控制理論與應用,1997,14(4):613-615.