基于神經(jīng)網(wǎng)絡的潛艇大機動水動力表達方式

周志剛，黃建偉，董根金

（武漢第二船舶設計研究所，湖北武漢 430064）

0 引言

潛艇在應急上浮過程中，容易出現(xiàn)大攻角運動狀態(tài)。特別是當艙室進水和舵卡事故，原重力與浮力平衡、縱傾力矩平衡都受到破壞時，潛艇垂向速度與前進速度相比并非小量，艇體運動相對水流形成大攻角。大攻角情況下的潛艇水動力非常復雜，表現(xiàn)出強烈的非線性特征。考慮到垂直面的運動參數(shù)是造成潛艇大機動水動力非線性的主要原因，因此可以將大攻角所產(chǎn)生的非線性水動力看作是潛艇垂向速度w和縱傾角速度q的函數(shù)。當前國內相關研究［1］的思路是采用低階多項式或樣條函數(shù)對潛艇大攻角機動運動水動力進行擬合，但其擬合精度或實用性等方面往往并不能讓人滿意。采用合適的方法準確表達潛艇大攻角機動運動的水動力，建立用于預報其大攻角機動運動狀態(tài)變化的數(shù)學模型，對潛艇的動力抗沉等有重大的指導意義。

本文根據(jù)已有的潛艇大攻角機動運動試驗資料，結合多項式和樣條函數(shù)的方法擬合其水動力的結果，指出了各自的局限性，設計了以攻角α（w'=sinα）和縱傾角速度q'作為輸入量，縱向力X'、垂向力Z'、縱傾力矩M'分別作為輸出量的3層BP神經(jīng)網(wǎng)絡，應用MATLAB 7.1神經(jīng)網(wǎng)絡工具箱對這一系列試驗數(shù)據(jù)的水動力進行了有效的擬合。

1 已有的潛艇大機動水動力表達形式

1.1 已有潛艇大機動水動力試驗數(shù)據(jù)特點

潛艇大攻角狀態(tài)的水動力是通過約束模擬試驗獲得的無因次量，包括2個運動狀態(tài)參數(shù)α和q'，水動力則為X'，Z'和M'，其中攻角α的范圍達到了±90°。將X'，Z'和M'的試驗點在空間展開，得到的是各力（矩）隨攻角和縱傾角速度變化的曲面，發(fā)現(xiàn)大攻角情況下的水動力隨α的變化表現(xiàn)出非常強烈的非線性，而隨q'的變化則近似為線性關系。如圖1所示，（a）圖為某一q'值下的縱傾力矩M'隨攻角α變化的曲線;（b）圖為某一攻角α值下的縱傾力矩M'隨q'變化的曲線。由圖還可以看到，試驗數(shù)據(jù)并非是均勻分布的，在水動力變化較大的一些攻角區(qū)間內試驗數(shù)據(jù)相對很少;而水動力在隨q'變化的曲線上，由于受到試驗條件的限制，有一大段區(qū)間內的水動力值無法通過試驗獲得。

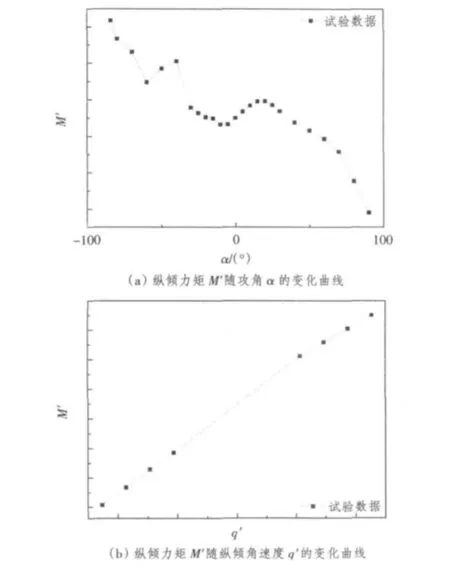
圖1 縱傾力矩M'試驗數(shù)據(jù)特點Fig.1Characteristic of M'testing data

1.2 多項式的水動力表達形式

根據(jù)相關資料的研究分析，在潛艇大攻角機動范圍內，宜采用二階多項式表達其水動力，以避免由于項數(shù)增加導致參數(shù)估計時的較大協(xié)方差，以及高階水動力導數(shù)的求取;而且這種表達形式與潛艇標準空間運動方程中水動力的表達形式保持一致，能從本質上反映潛艇水動力的物理特性。圖2給出了在攻角±90°范圍內，經(jīng)這種方法處理后在某一縱傾角速度下縱傾力矩隨攻角變化的擬合曲線。

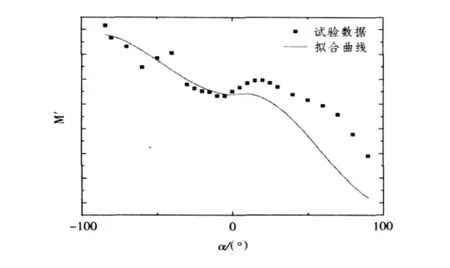
圖2 縱傾力矩M'的多項式表達擬合曲線Fig.2Fitted curf of M'by polynomial

如圖2所示，多項式表達的水動力只能大致反映其在整個攻角范圍內的變化趨勢，但是其擬合精度顯然不足以建立準確的數(shù)學仿真模型，從而滿足實艇操縱性預報的要求。如果采取分段低階多項式的形式表達水動力，雖然擬合精度可以提高一些，但在各區(qū)間段的端點不能保持光滑過渡，處理試驗數(shù)據(jù)時也會帶來相當?shù)穆闊Ｓ纱丝梢姡碗A多項式形式不適用于在整個攻角范圍內表達潛艇大機動水動力。

1.3 樣條函數(shù)的水動力表達形式

利用樣條函數(shù)建立非線性水動力數(shù)學模型的優(yōu)點是，可以用低階多項式很好地逼近各種非線性。樣條函數(shù)模型也是基于Bryan準定常假設的飛機大攻角氣動力常用代數(shù)模型之一。在大攻角下，飛機的縱向氣動力系數(shù)主要是攻角α的非線性函數(shù)，只需采用單變量的樣條函數(shù)模型;橫向氣動系數(shù)對攻角α和側滑角β都是非線性的，必須采用雙變量的樣條函數(shù)模型［4］。從前面試驗數(shù)據(jù)的分析知道，潛艇垂直面大攻角機動運動水動力的非線性只是體現(xiàn)在攻角α上，實踐證明采用3次樣條函數(shù)插值即可滿足工程應用要求，保證了擬合出來的水動力在試驗點處二階連續(xù)。在區(qū)間［α1，αn］上關于變量α的3次樣條函數(shù)［5］可以表示為:

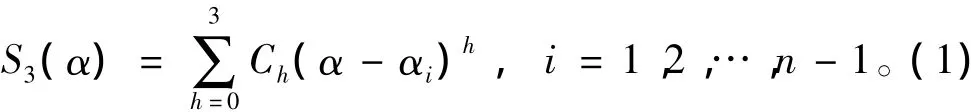
樣條節(jié)點α1，α2，…，αn滿足α1＜α2＜…＜αn的順序。Ch為樣條的常數(shù)項。圖3給出的是基于該函數(shù)形式擬合的某一縱傾角速度下縱傾力矩隨攻角變化的擬合曲線。

如圖3所示，樣條函數(shù)擬合的水動力嚴格地經(jīng)過了每1個試驗點，因而具有較高的精度。但這種高精度是建立在水動力試驗數(shù)據(jù)的高準確度上，樣條函數(shù)形式并不利于消除試驗數(shù)據(jù)本身的誤差，且表達完整的水動力情況需要大量的試驗數(shù)據(jù)，一旦數(shù)據(jù)偏少或分布極其不均，擬合的曲線可能會出現(xiàn)不必要的“振蕩”，表現(xiàn)在空間上就是一些凸凹不平的坑，因而采用樣條函數(shù)形式表達潛艇大機動水動力也有局限性。

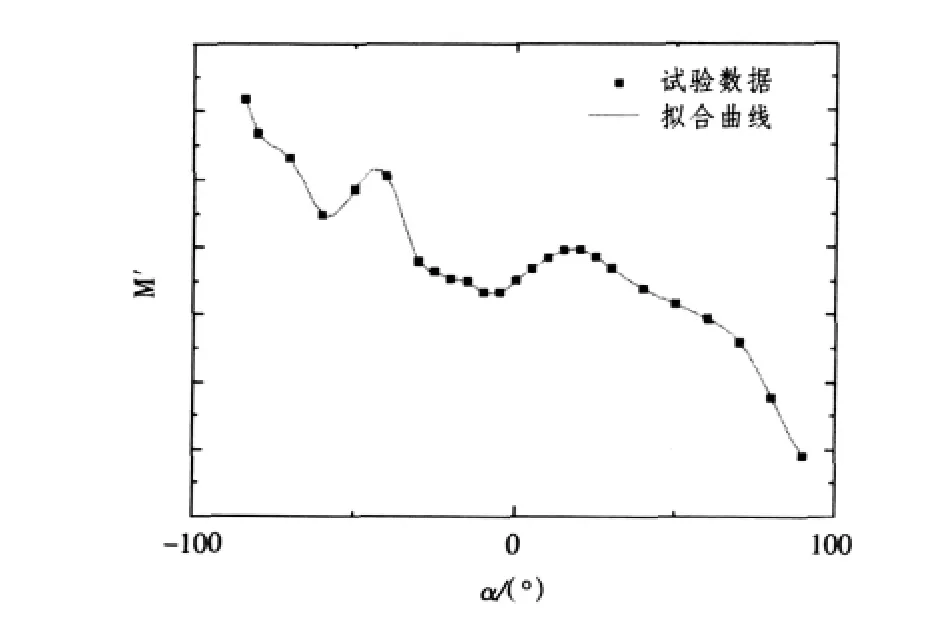
圖3 縱傾力矩M'的樣條函數(shù)表達擬合曲線Fig.3Fitted curf of M'by spline interpolation

綜上所述，如何應用合理的表達方式在樣本數(shù)據(jù)較少的情況下準確預報潛艇大機動水動力，以及保證其在沒有試驗數(shù)據(jù)的區(qū)間具有較好的泛化能力，并且能推廣到大機動運動整個攻角區(qū)間，具有非常重要的工程應用價值，值得進一步研究。

2 潛艇大機動水動力表達

2.1 BP神經(jīng)網(wǎng)絡原理及構建過程

BP網(wǎng)絡是1種單向傳播的多層前向網(wǎng)絡，本文采用的3層BP網(wǎng)絡結構如圖4所示。輸入層為2個神經(jīng)元，輸出層為1個神經(jīng)元，設隱層神經(jīng)元數(shù)為N，隱層傳遞函數(shù)采用f1（·），輸出層傳遞函數(shù)采用f2（·），誤差函數(shù)采用E（·），則網(wǎng)絡的學習過程可用下列函數(shù)描述:

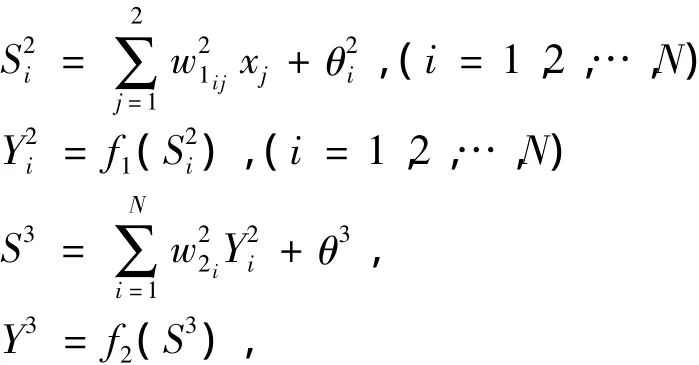
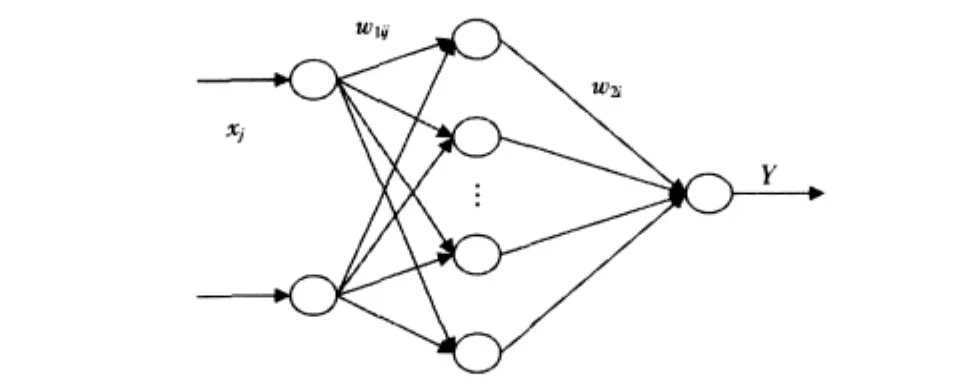
圖43 層BP網(wǎng)絡結構圖Fig.4Frame of BP neural net with three layers

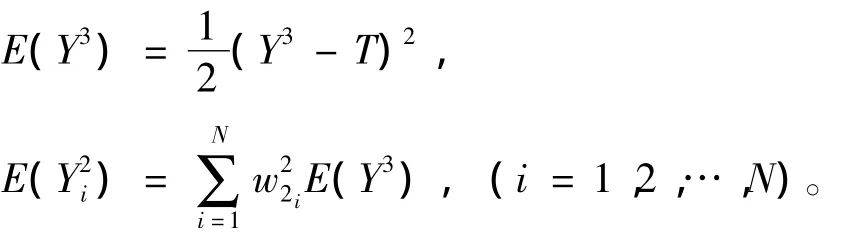
學習過程中將誤差反向傳播計算，對網(wǎng)絡各相鄰節(jié)點的連接權值w和偏置θ進行調整，使誤差函數(shù)E（·）沿負梯度方向下降，然后再轉入正向傳播過程，反復迭代，直到誤差達到穩(wěn)態(tài)或小于給定的值為止。

當輸入、輸出變量以及隱層層數(shù)明確的情況下，構建BP神經(jīng)網(wǎng)絡的一般步驟如下:

1）對樣本的歸一化處理，以消除各變量的量綱影響，MATLAB中命令premnmx可將樣本數(shù)據(jù)處理到區(qū)間（－1，1）上。

2）根據(jù)神經(jīng)網(wǎng)絡的用途選擇相應的輸出層傳遞函數(shù)，根據(jù)數(shù)據(jù)的特點選擇合適的隱層傳遞函數(shù)。

3）設計隱層最佳單元數(shù)，一般是在經(jīng)驗公式范圍內采用試湊法尋找［5］。隱層神經(jīng)元的個數(shù)是神經(jīng)網(wǎng)絡訓練成敗的關鍵，不合理的單元個數(shù)容易出現(xiàn)“欠擬合”或“過擬合”的現(xiàn)象。

4）選擇合適的訓練函數(shù)，MATLAB提供的BP神經(jīng)網(wǎng)絡的訓練函數(shù)有數(shù)十種。

2.2 建立潛艇大機動水動力表達的BP神經(jīng)網(wǎng)絡

1）樣本預處理與傳遞函數(shù)選擇本文采用更一般的轉換公式

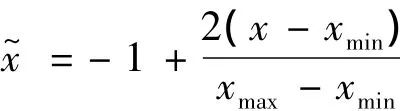
隱層傳遞函數(shù)取反對稱形式的雙曲正切函數(shù)，輸出層傳遞函數(shù)取純線性函數(shù)。

2）隱層神經(jīng)元數(shù)的確定

對于本組潛艇大機動的試驗數(shù)據(jù)，采用經(jīng)驗公式設計的隱層單元數(shù)，其建立的BP神經(jīng)網(wǎng)絡模型并不能獲得滿意的效果。最佳神經(jīng)元個數(shù)的取值范圍必將擴大，盲目摸索非常耗費人力和時間。本文采用近似于窮舉法來選擇隱層神經(jīng)元的個數(shù)，即先確定1個較大的隱層神經(jīng)元數(shù)目的范圍，再從較少神經(jīng)元開始訓練，然后逐漸增加神經(jīng)元的個數(shù)，重復學習訓練。這個過程非常類似于人腦對事物認知從簡單到復雜的情況，每一步的訓練過程都以上一步的訓練結果為初值，相當于對上次學習有所“記憶”，整個確定最佳隱層神經(jīng)元個數(shù)的過程也可以看作是循環(huán)強化學習的過程，這樣不僅能完全自適應地找到最佳隱層單元數(shù)，而且還獲得了非常高的訓練精度。這一點可以對比應用最佳隱層只進行1次訓練的擬合曲線和循環(huán)訓練后的擬合曲線來驗證，如圖5所示。

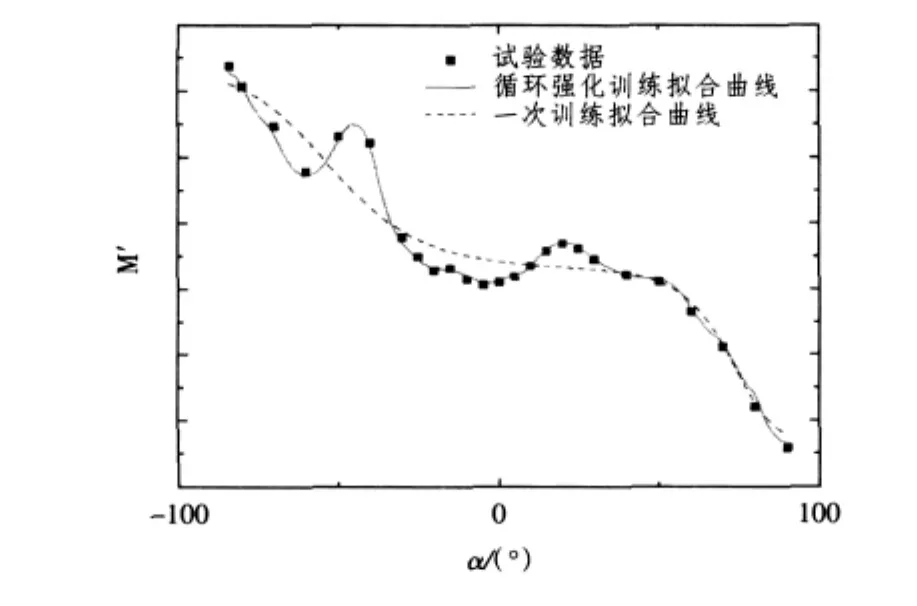
圖5 不同訓練次數(shù)擬合曲線對比Fig.5Compare of fitted curf by different train time

考慮到潛艇在整個大攻角范圍內機動運動時的實際應用情形，為了保證網(wǎng)絡在正常機動和大攻角機動狀態(tài)下均具有良好的適用性，本文還設計了2個均方差性能參數(shù)mse±30°和mse±90°，以及擬合水動力隨攻角變化曲線的拐點個數(shù)來控制循環(huán)次數(shù)，一旦同時達到這3個參數(shù)設定的值即認為網(wǎng)絡已經(jīng)訓練成熟，其中，mse±30°和mse±90°分別用于表征（－30°，30°）和（－90°，90°）區(qū)間內的網(wǎng)絡預報值與試驗值的均方差。

3）訓練函數(shù)的確定及其預測誤差

BP神經(jīng)網(wǎng)絡訓練函數(shù)實質上基于最速下降反向傳播算法經(jīng)過改進衍化而成。例如，在誤差反向傳播的基礎上，將每1個權值的變化加上1項正比于前次權值變化量的值，并自適應學習速率的訓練函數(shù)traingdx;基于數(shù)值優(yōu)化方法的算法，結合了梯度下降法和牛頓法在誤差下降搜索方向的優(yōu)點，由Levenberg和Marquardt提出的訓練函數(shù)trainlm;同樣以L-M優(yōu)化理論為基礎對網(wǎng)絡權值和偏置進行調整，而將誤差性能函數(shù)mse修改為包含有網(wǎng)絡權值和偏置均方值的誤差性能函數(shù)msereg的Bayesian正則化訓練函數(shù)trainbr，其中:

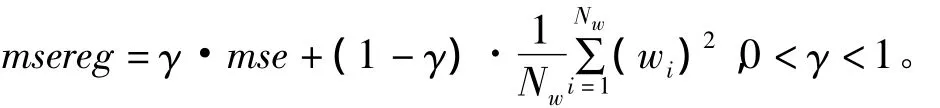
實驗結果顯示，網(wǎng)絡選擇這3種訓練函數(shù)相對于其他訓練函數(shù)在收斂精度上具有絕對的優(yōu)勢，本文將相應的訓練后最佳隱層神經(jīng)元個數(shù)N和設定的均方差性能參數(shù)mse±30°和mse±90°列于表1中。

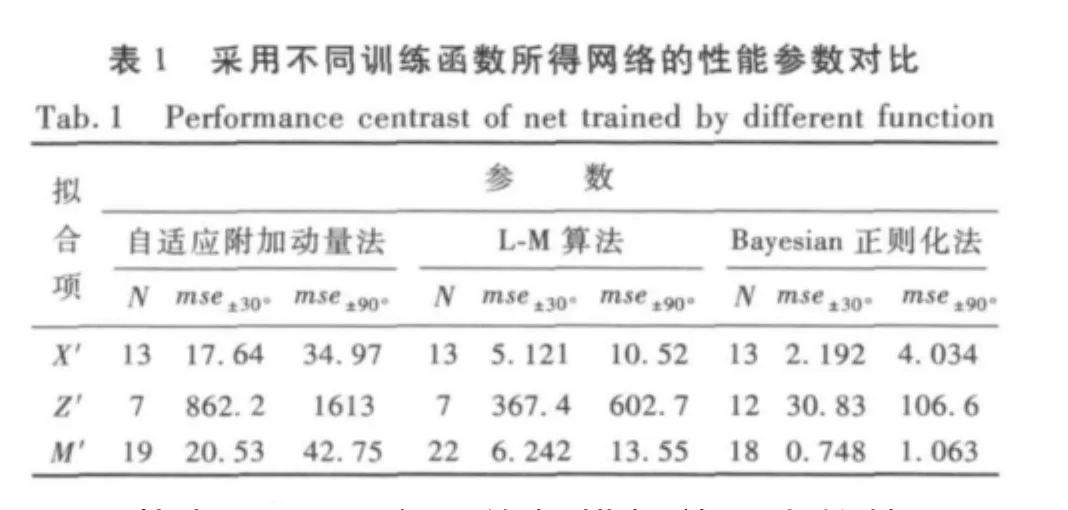
從表1可見，在網(wǎng)絡規(guī)模相差不大的情況下，Bayesian正則化方法訓練的BP神經(jīng)網(wǎng)絡相對于其他2種方法在擬合精度上幾乎提高了1個數(shù)量級，而且分析其誤差性能函數(shù)msereg可知，這種方法本身能使網(wǎng)絡獲得較小的權值和偏置，使得網(wǎng)絡的響應趨于平滑，減小了過度擬合的可能性。圖6給出了采用函數(shù)trainbr訓練后縱向力、垂向力和縱傾力矩隨攻角和縱傾角速度變化的曲面。

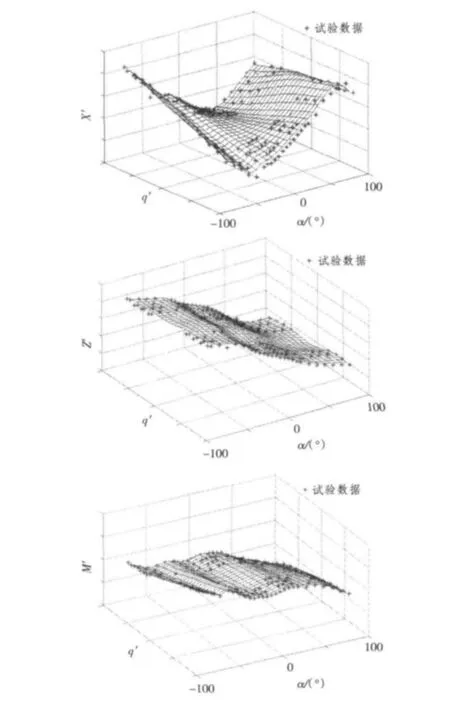
圖6 Bayesian正則化法訓練的BP神經(jīng)網(wǎng)絡擬合曲面Fig.6Fitted curf of hydrodynamics based on Bayesian-BP neural network

可以看到，所建立的網(wǎng)絡在整個潛艇大機動范圍內顯示了良好的推廣性，沒有出現(xiàn)類似樣條函數(shù)表達形式獲得曲面的凸凹不平的坑，而且神經(jīng)網(wǎng)絡模型計算值與數(shù)據(jù)樣本的相關系數(shù)分別達到了RX=0.995 8，RZ=0.999 6，RM=0.998 9。

2.3 潛艇大機動水動力不同表達方式比較

圖7所示從上到下依次為樣條函數(shù)、Bayesian正則化法BP神經(jīng)網(wǎng)絡和多項式擬合的縱向力隨攻角和縱傾角速度變化曲面。這里3個曲面在垂直方向的距離是為了便于比較圖形而設置的，并不代表任意兩者之間存在這樣一個差值。由圖示效果可以直觀得出如下結論:Bayesian正則化法BP神經(jīng)網(wǎng)絡對數(shù)據(jù)樣本集較小的潛艇大機動水動力函數(shù)逼近能力優(yōu)異，是一種優(yōu)于多項式和樣條函數(shù)形式表達潛艇大機動運動水動力的方法。

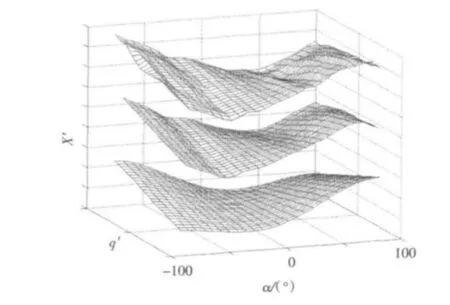
圖7 3種表達方式對縱向力的擬合曲面對比圖Fig.7Compare of X'fitted curf by three means

3 結語

1）潛艇的大攻角機動運動表現(xiàn)出強烈的非線性特征，采用多項式、樣條函數(shù)形式表達其水動力具有各自明顯的局限性或不足，本文應用BP神經(jīng)網(wǎng)絡模型擬合了整個大攻角范圍內的水動力試驗值，展示了其作為一種函數(shù)逼近工具的優(yōu)越性;

2）本文建立的BP神經(jīng)網(wǎng)絡采取了循環(huán)強化訓練的方法，以及通過近似窮舉法設計神經(jīng)網(wǎng)絡隱層單元數(shù)，實踐表明這些處理方法的方便、可行性;在確定訓練函數(shù)過程中，發(fā)現(xiàn)Bayesian正則化方法具有較高的網(wǎng)絡預報精度和網(wǎng)絡泛化能力，適合于樣本數(shù)據(jù)集較小的潛艇大機動水動力擬合;

3）本文采用BP神經(jīng)網(wǎng)絡技術表達潛艇大攻角機動運動水動力的研究工作，為合理應用水動力試驗數(shù)據(jù)并建立其數(shù)學仿真模型提供了一種新的思路，具有廣闊的工程應用前景。

［1］張華，吳寶山．扁平型潛水器空間大機動數(shù)學模型研究［A］．2004年船舶水動力學學術會議論文集［C］．2004．122－129．

［2］田雨波．混合神經(jīng)網(wǎng)絡技術［M］．北京:科學出版社，2009．38－48．

［3］從爽．面向MATLAB工具箱的神經(jīng)網(wǎng)絡理論與研究［M］．合肥:中國科學技術大學出版社，2009．63－100．

［4］汪清，蔡金獅．飛機大攻角氣動力建模研究進展［J］．氣動實驗與測量控制，1994，（9）:7－16．

［5］李紅．數(shù)值分析［M］．武漢:華中科技大學出版社，2006．40－49．

［6］飛思科技產(chǎn)品研發(fā)中心．神經(jīng)網(wǎng)絡理論與MATLAB7實現(xiàn)［M］．北京:電子工業(yè)出版社，2005．99－104．