稀有事件logistic回歸在醫學研究中的應用*

趙晉芳 羅天娥 范月玲 曾 平 仇麗霞 劉桂芬△

如果疾病的發生水平很低，極為不常見，病例在人群中所占比重就非常小，那么稱這個醫學事件為稀有事件。如果我們采用常見的現況流行病調查方法或隊列研究研究這種疾病，就會導致收集的數據中病例數與非病例數很不均衡。比如要探索研究該疾病的影響因素，通常的做法是對病例和非病例的兩類人群建立logistic回歸模型，然而由于資料中的病例所占的比例遠遠低于非病例的比重，這就給稀有事件的統計分析帶來一系列問題，在這種情況下仍采用常規的logistic回歸方法就不適合了。本文將主要探討一種適用于解決醫學現象研究中稀有事件的logistic回歸模型，它校正了普通logistic回歸在參數估計、統計推斷和概率預測方面都有可能存在的缺陷。

原理和方法

1．稀有事件logistic回歸

醫學研究中，當隨機反應變量Y的結果表現為二分類變量時，如發病(Y=1)和不發病(Y=0)，感染(Y=1)和不感染(Y=0)，若感染(Y=1)的概率P受到因素影響時，可表示為

x'為暴露因素，α，β分別為截距項和回歸參數向量。logistic回歸系數的極大似然估計值^β具有一致性、漸近有效性和漸近正態性的性質，并且在結果變量Y兩類取值頻率相等時的檢驗效率是最高的〔1－3〕。

但在稀有事件分析中，由于存在大量Y=0的記錄，而Y=1的例數卻很少，這就會導致一般的logistic回歸在參數估計、統計推斷和概率預測方面都可能存在一定的缺陷。下面介紹一種適合醫學中稀有事件的logistic回歸(rare event logistic，re-logistic)，其基本思想是在普通logistic回歸結果基礎上給予適當的校正。

(1)先驗校正

先驗校正(prior correction)是在普通logistic回歸最大似然估計值的基礎上，結合總體中Y=1的概率τ，以及樣本中Y=1的比例(或叫抽樣概率)ˉy對回歸系數的最大似然估計值進行校正〔4〕。~

α為經過先驗校正的截距項。先驗校正的思想最初源于 Prentice和 Pyke(1979)，Manski和 Lerman(1977)，以及Daniel McFadden尚沒有公開發表的一篇文獻〔5－7〕。先驗校正需要已知總體率τ，關于總體中Y=1的概率τ的先驗信息可以從普查、大樣本的隨機抽樣研究或病例－隊列研究中得到。

(2)加權校正

研究中可能存在由于樣本選擇的原因而導致總體概率τ和樣本概率ˉy之間有差異，而加權校正(weight correction)正是要對樣本觀察單位給予合適的權重來補償因選擇偏倚造成的影響。對樣本中Y=1的觀察單位給予權重w1=τ/ˉy，Y=0的觀察單位給予權重w0=(1－τ)/(1－ˉy)。則logistic回歸有以下的加權對數似然函數:

最大化(3)式即可得到參數的最大似然估計值。研究表明，加權校正在大樣本和模型指定有誤時要優于先驗校正〔8〕，而在小樣本時，先驗校正要優于加權校正，但這種差別不是很大〔9，10〕。

(3)稀有事件回歸系數的MCN校正

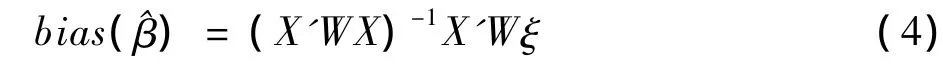
α和β的最大似然估計值在小樣本時是有偏的，而且稀有事件會進一步放大這種偏倚。在小樣本稀有事件中，先驗校正和加權校正仍存在一定的偏差，尚需要進行進一步的校正。小樣本的稀有事件回歸系數的偏倚量(bias)〔4，11，12〕:)式中ξi=0.5Qii［(1+w1)^πi－w1］，Qii為矩陣Q=X(X'WX)－1X'的對角元素，W=diag{^πi(1－^π)wi}。從式(4)可見，實際上偏倚量bias(^β)就是以X為自變量，ξ為應變量，W為權重的回歸方程的系數的加權最小二乘估計值。校正的參數估計值為:

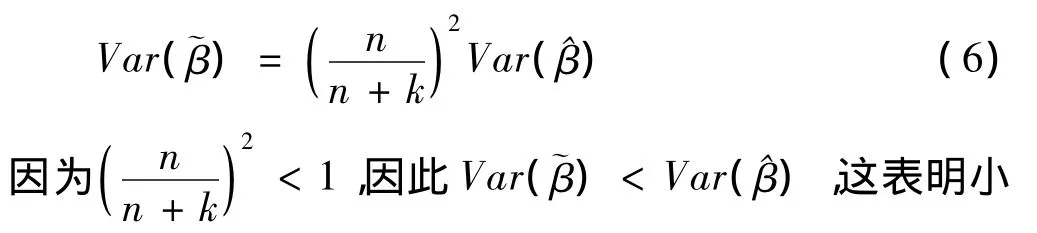
校正的參數方差矩陣為:樣本的稀有事件回歸系數的校正不但得到了無偏的參數估計量，而且還降低了方差，其統計性質優于前者。這種校正方法又被Gary King和Lang che Zeng簡稱為MCN校正(McCullagh Nelder Correction)。

(4)稀有事件概率估計

稀有事件回歸系數的最大似然估計值^β本身是有偏估計值，因此個體Y=1的概率估計也是有偏的;即使^β是無偏估計值，也并不能保證概率估計值就是最優的。可以選擇下面的公式估計稀有事件中Y=1的概率:β*為結合啞變量(integration dummy)。式(7)可以看做 ~β 抽樣分布下 ~P(Y=1|~β)的期望值，而 ~P(Y=1|~β)是Pi=P(Y=1|β)的點估計值。式(7)亦可以近似表示為:P(Yi=1)≈~Pi+Ci或 P(Yi=1)≈~Pi－Ci。其中，Ci稱為校正因子(correction factor)，計算公式為:

在滿足一定條件下，~Pi－Ci是近似無偏的，但是模擬研究顯示~Pi+Ci有更小的均方誤。~Pi－Ci稱為Pi=P(Y=1|β)的近似無偏估計值(approximate unbiased estimator)，~Pi+Ci稱為近似 Bayes估計值(approximate Bayesian estimator)〔4〕。有研究顯示，除了某些特殊情況，如多個小樣本的meta分析中，近似無偏估計值要好于Bayes估計值外，多數應用中，Bayes估計值要優于近似無偏估計值。

2．非嵌套模型Vuong檢驗

采用Vuong(1989)提出的非嵌套模型檢驗(nonnested models test)〔13－15〕來檢驗 logistic 回歸和稀有事件logistic回歸的非嵌套關系。

式中，^Prelogit(yi|xi，wi)和 ^Plogit(yi|xi)分別為稀有事件logistic回歸和普通 logistic回歸預測概率。根據Vuong，模型1相對于模型2的非嵌套模型檢驗的統計量為

實例分析

通過與山西省疾病預防控制中心聯合，對山西省運城市五個項目防治縣的316例HIV/AIDS患者進行結核病的篩查。欲對HIV/AIDS患者是否患結核病進行分析，結果如下。Min Max

表1 HIV/AIDS患者資料簡單描述ˉ

n x±s

表2 HIV/AIDS患者資料變量編碼及構成

HIV/AIDS患者中大多是初中文化程度，占總患者的66.14%(209/316);患者的平均年齡為41.6歲，以壯年為主;HIV/AIDS患者 CD4計數的均值為317.85(個/μl)，低于正常人水平，其最大值為1125(個/μl)，最小值為 1(個/μl)，標準差為 183.80(個/μl)，變異較大，因此對CD4作自然對數轉換，并在以后的分析中代替CD4作為自變量，且仍用CD4作為其變量名。

調查的316例HIV/AIDS患者中僅有11人是結核感染者，感染率大約為3.48%。因此我們認為分析樣本中HIV/AIDS患者感染結核是稀有事件。

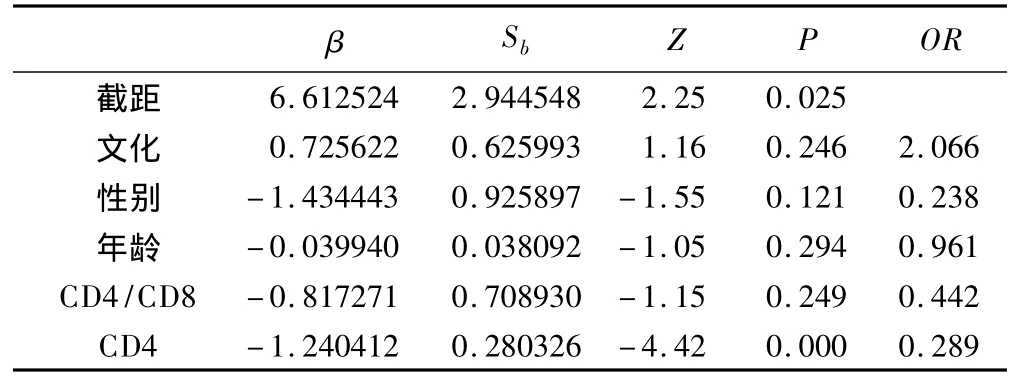
表3 普通logistic回歸參數估計

普通logistic回歸參數估計顯示HIV/AIDS患者CD4計數有統計學意義，與是否感染結核病有關系，CD4計數對數值每增加一個單位，HIV/AIDS患者感染結核的危險性降低71.1%［1－exp(－1.240412)］，即CD4計數水平越高HIV/AIDS患者患結核病的可能性越小。

表4 logistic回歸先驗校正

logistic回歸先驗校正是在普通logistic回歸參數估計的基礎上對截距項做了校正，其他回歸系數估計值和標準誤均未發生改變。以往報道表明，感染了結核菌的HIV/AIDS患者每年發展為結核病的機會為7%，據山西省權威機構2008年底提供的數字顯示，HIV/AIDS患者的結核發病率估計在5%左右，故本次研究τ取值為0.05。校正后的截距為:

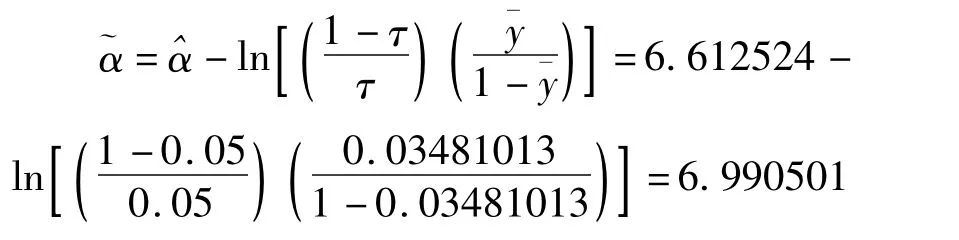
表5 logistic回歸MCN先驗校正

logistic回歸MCN先驗校正參數估計CD4計數對數值每增加一個單位，HIV/AIDS患者感染結核的危險性降低68.0%。

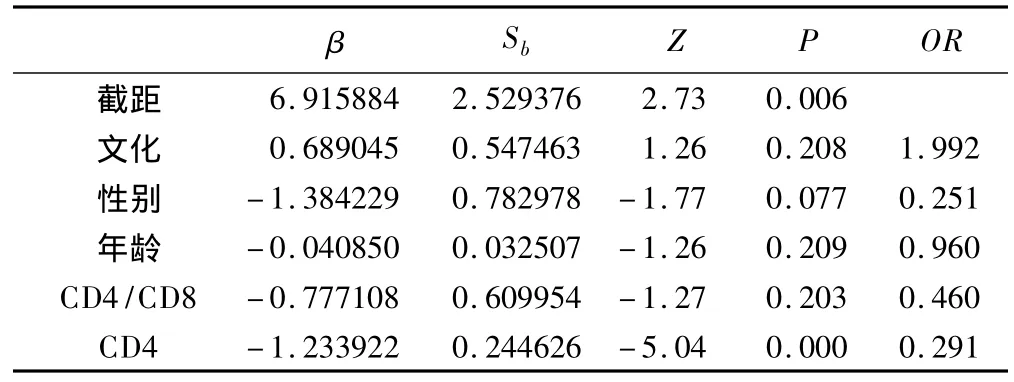
表6 logistic回歸加權校正

在普通logistic回歸的基礎上對樣本中的每個觀察單位進行加權校正，其中:w1=τ/ˉy=0.05/0.03481013，w0=(1－τ)/(1－ˉy)=(1－0.05)/(1－0.03481013)。

加權校正logistic回歸表明CD4計數對數值每增加一個單位，HIV/AIDS患者感染結核的危險性降低70.9%。

加權logistic回歸MCN校正結果表明CD4計數對數值每增加一個單位，HIV/AIDS患者感染結核的危險性降低67.8%。

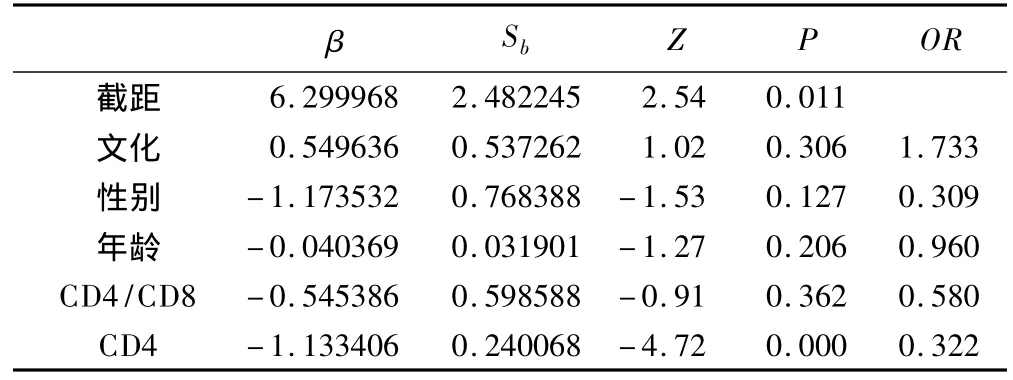
表7 logistic回歸MCN加權校正

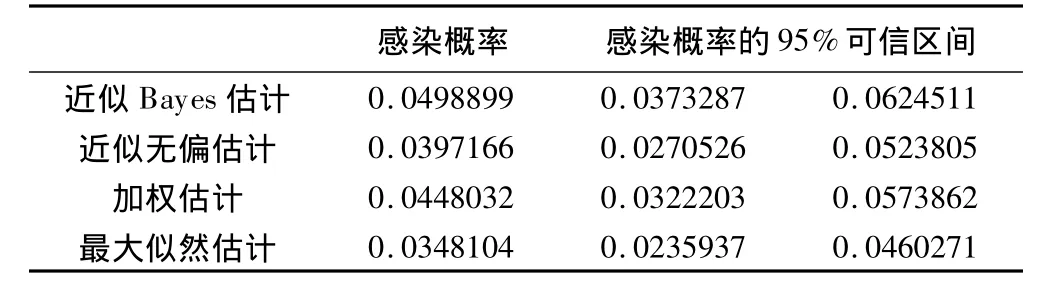
表8 HIV/AIDS患者結核感染概率估計

我們采用以上的幾種模型估計本次調查樣本的HIV/AIDS患者結核感染率，不同方法的HIV/AIDS患者結核感染概率估計顯示，最大似然估計的感染概率最小，即普通logistic回歸低估了感染概率，其他三種估計方法的感染概率估計值有所提高，彌補了稀有事件中傳統的估計方法可能會低估事件Y=1的預測概率的缺憾，即校正后感染概率估計偏倚減少。加權估計和近似Bayes估計的感染概率估計值接近5.00%。

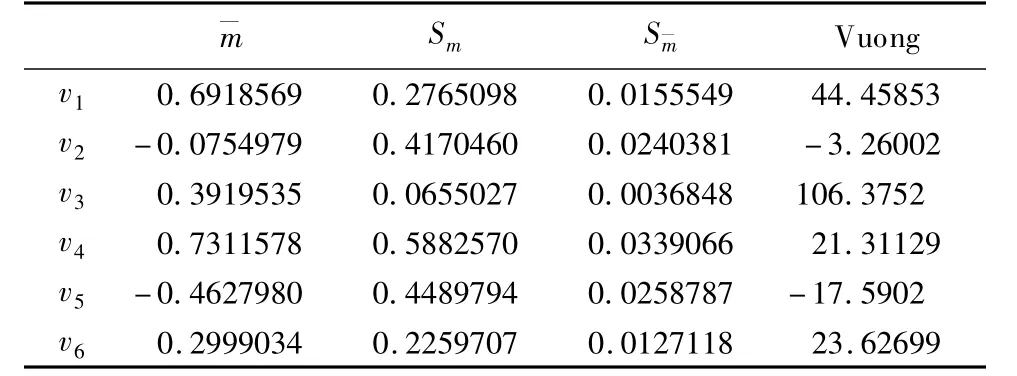
表9 不同校正方法的logistic回歸和普通logistic回歸的Vuong檢驗

PPLUS表示近似Bayes估計概率，PJIAN表示近似無偏估計概率，PROB表示加權估計概率，P0為普通logistic回歸預測概率。

Vuong檢驗顯示加權校正和近似Bayes估計都要優于普通logistic回歸、近似無偏估計;近似Bayes估計優于加權校正;而近似無偏估計不如普通logistic回歸。

綜上，Vuong檢驗和概率預測結果顯示近似Bayes估計得到的結果最優。

討 論

醫學研究中經常遇到二分類反應變量資料采用logistic回歸分析，若應變量兩類取值頻率相差特別懸殊時，普通logistic回歸不僅參數估計有偏，并且可低估稀有事件的發生概率。通過稀有事件logistic回歸校正參數和概率估計值來解決這個問題，效果較好。實例分析結果表明，在稀有事件的分析中，不管是在模型的整體表現或者是模型的預測預報方面，稀有事件的logistic回歸確實要更優于普通的logistic回歸。因此對于醫學中很多不常見疾病的研究，稀有事件的logistic回歸是一種值得推廣應用的統計模型。當然，對于某一個醫學事件要根據具體的情況從專業的角度判斷其是否是稀有或罕見事件，從實際應用看確定這一點并不難。

稀有事件logistic的校正方法可以在Gary King和Langche Zeng 2001年推出的 STATA程序——relogit中實現，relogit是一種非官方的程序需要下載安裝后才可以使用。不同模型間的Vuong檢驗目前尚無專門的程序，本文通過SAS9.1軟件編程實現非嵌套模型的比較。

1．Manski CF，McFadden D．Structural analysis of discrete data with econometric applications．MA:Cambridge:MIT Press，1981:51-111．

2．Imbens GW．An efficient method of moments estimator for discrete choice models with choice-based sampling．Econometrica，1992，60(5):1187-1214．

3．陳峰．醫用多元統計分析方法．北京:中國統計出版社，2001．

4．King G，Zeng LC．Logistic regression in rare events data．Political analysis，2001，9(2):137-163．

5．Prentice RL，Pyke R．Logistic disease incidence models and case-control studies．Biometrika，1979，66(3):403-411．

6．Manski CF，Lerman SR．The estimation of choice probabilities from choice based samples．Econometrica，1977，45(8):1977-1988．

7．Manski CF，McFadden D．Structural analysis of discrete data with econometric applications．MA:Cambridge:MIT Press，1981:2-50．

8．Xie Y，Manski CF．The logit model and response-based samples．Sociological Methods Research，1989，17(3):283-302．

9．Amemiya T，Vuong QH．A comparison of two consistent estimators in the choice-based sampling qualitative response model．Econometrica，1987，55(3):699-702．

10．Scott AJ，Wild CJ．Fitting logistic models under tuberculosis-control or choice based sampling．J R Statist Soc B，1986，48(2):170-182．

11．McCullagh P，Nelder JA．Generalized Linear Models．New York:Chapman ＆ Hall，CRC，1999．

12．King G，Zeng LC．Explaining rare events in international relations．International Organization，2001，55(3):693-715．

13．Strazzera E，Genius M．Evaluation of likelihood based tests for non-nested dichotomous choice contingent valuation models．Working Paper CRENoS，2000:2-28．

14．Greene WH．Accounting for excess zeros and sample selection in Poisson and negative binomial regression models．Working Paper No．EC-94-10，Department of Economics，Stern School of Business，New York University，1994．

15．Vuong QH．Likelihood ratio tests for model selection and non-nested hypotheses．Econometrica，1989，57(2):307-333．