重復測量計數(shù)資料的隨機效應ZINB模型*

趙麗華 劉桂芬 田嬌妮

Poisson模型是計數(shù)資料分析的基礎模型，但在醫(yī)學研究中，經(jīng)常會遇到某事件發(fā)生次數(shù)的資料中含有大量的零，即觀察個體在單位時間、單位體積內(nèi)未觀察到相應事件的發(fā)生次數(shù)。大量的零計數(shù)存在，且其比例超過Poisson分布的預測概率。Cohen(1963)、Johnson 和 Kotz(1969)早就注意到零過多現(xiàn)象〔1，2〕，但直到20世紀90年代，Lambert(1992)才首次建立了協(xié)變量零膨脹Poisson模型，并探討了參數(shù)極大似然估計及大樣本性質〔3〕。Greene(1994)提出了模型參數(shù)方差的BHHH估計，應用ZINB模型研究了消費者銀行信用卡不良記錄資料〔4〕。Greene(2000)將零膨脹模型引進了新版的Limdep 7．0中〔5〕。近年零膨脹模型逐漸地被應用到交通、政治、微觀經(jīng)濟等研究領域中，本文引入隨機效應ZINB模型，闡明醫(yī)學領域零過多和過度離散問題并存時重復測量計數(shù)數(shù)據(jù)的分析方法及其應用。

模型原理介紹

1．固定效應ZINB模型(FE-ZINB)

ZINB模型的基本思想是把某事件發(fā)生次數(shù)看成兩個過程:第一過程對應零事件的發(fā)生，假定零事件以概率pi發(fā)生，在這個過程中認為個體取值為0或非0，因此能夠解釋數(shù)據(jù)中可能存在的過多0的原因;第二過程對應事件數(shù)的發(fā)生過程，假定對應事件數(shù)以概率1－pi發(fā)生，在這個過程中個體的取值可以為0或正的事件數(shù)，并且服從均值為λi的負二項分布。

FE-ZINB模型的概率分布如下:

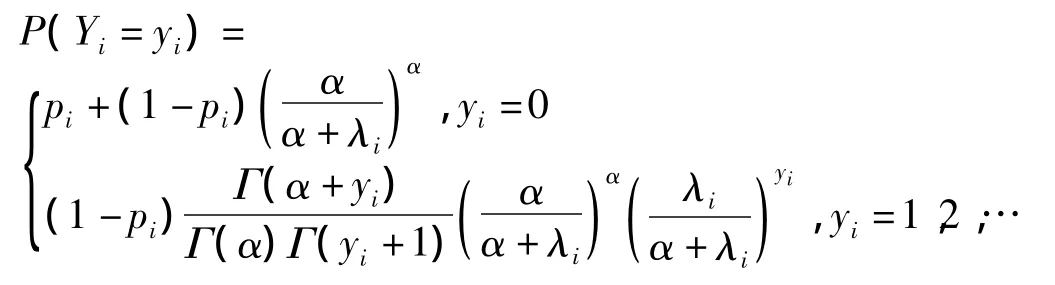
2．隨機效應ZINB模型(RE-ZINB)

重復測量資料是指同一個體在不同時點或部位多次測量得到的，由于同一個體j個觀察值間存在相關性，提供的信息量不及j個獨立的觀察值，相關性越高，提供的信息量就越少。分析中若忽略資料的非獨立性，有可能導致錯誤的分析結論〔6〕。

設 yij為第 i個體第 j次的觀察值，i=1，2，3，…，n，j=1，2，3，…，k，隨機效應 ZINB 模型可表示為

當α→0時，RE-ZINB模型就退化為RE-ZIP模型。

隨機效應ZINB模型記作

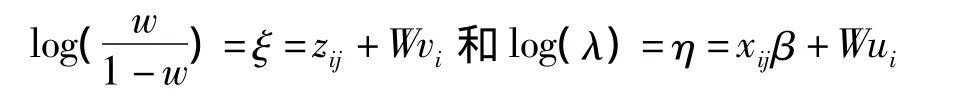
模擬研究

假定計數(shù)反應變量yij服從如下的混合概率分布〔7〕:

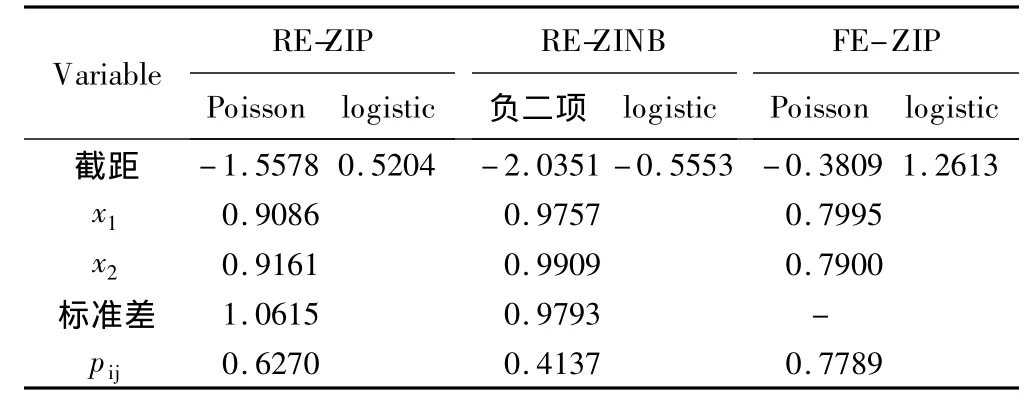
表1 模擬數(shù)據(jù)三種模型參數(shù)估計結果

由于RE-ZINB模型考慮了隨機效應、數(shù)據(jù)中存在過多零計數(shù)以及過度離散問題，表1可見RE-ZINB參數(shù)和pij的估計值都很接近模擬真值，擬合結果最好。固定效應ZIP模型雖考慮了過多零計數(shù)，但忽略了隨機效應，這樣增大了自由度，而導致高估常數(shù)項和pij。隨機效應ZIP模型雖考慮了隨機效應但忽略了數(shù)據(jù)的過度離散，其結果低估了常數(shù)項。由此若計數(shù)資料存在相關結構，應考慮隨機效應模型;若還存在零計數(shù)過多以及過度離散問題時，選擇隨機效應ZINB模型擬合較好。

實例分析

某研究組采用離體心臟灌流實驗，探討A(對照藥)、B(處理藥物1)、C(處理藥物2)三種藥物的藥效關系。隨機抽取月齡相同體重相近的大白鼠36只，隨機分為3組，處死大白鼠取心臟置于離體心臟灌流液實驗裝置中，觀察不同藥物對離體心臟活動的影響。取前五分鐘內(nèi)心律不齊的平均次數(shù)作為每只老鼠的基線指標，分別在灌流液中加入一定劑量的A、B、C三種藥物后，每隔一分鐘記錄大鼠心律不齊發(fā)生的次數(shù)，連續(xù)觀察并記錄10次。整個實驗過程中人工控制實驗灌流裝置，保證離體心臟在觀察期間內(nèi)灌流壓力、溫度、酸堿度等存活條件及藥物濃度保持不變。

大鼠離體心臟灌流實驗心律不齊平均發(fā)生次數(shù)為1.567次，離體心臟心律不齊次數(shù)的統(tǒng)計描述見表2，心律不齊次數(shù)的均數(shù)和方差相差較大，這可能是由于數(shù)據(jù)中存在的0次心律不齊比例過多而導致的。本實驗觀察心律不齊發(fā)生0次數(shù)的頻率為46．94%，而理論Poisson與負二項分布的零概率分別為20．87%和38．96%，遠遠低于實際頻率，因此對心律不齊發(fā)生次數(shù)資料不能簡單地擬合基礎計數(shù)模型，而應建立隨機效應零膨脹計數(shù)模型，模型擬合結果見表3。

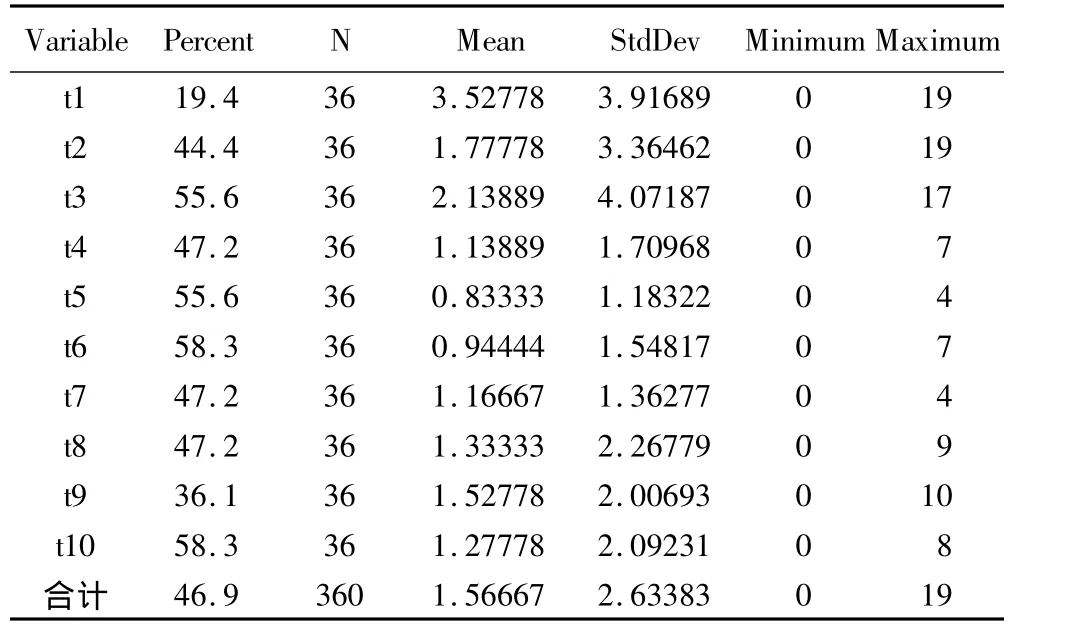
表2 離體心臟心律不齊次數(shù)的統(tǒng)計描述

離體心臟心律不齊數(shù)據(jù)的四種模型擬合優(yōu)度指標表明(表3)，RE-ZINB模型BIC值最小，而AIC和LL指標結果與BIC結果相同，仍以RE-ZINB最優(yōu)。結合資料數(shù)據(jù)結構和專業(yè)知識，我們認為，對于離體心臟心律不齊數(shù)據(jù)，擬合RE-ZINB模型效果最優(yōu)。RE-ZINB模型負二項部分的隨機效應有統(tǒng)計學意義，表明不同大鼠心律不齊發(fā)生次數(shù)差別有意義。

表3 離體心臟心律不齊數(shù)據(jù)的四種模型擬合結果評價

離體心臟心律不齊數(shù)據(jù)的四種模型參數(shù)估計結果表明(表4)，RE-ZINB模型中l(wèi)ogistic回歸參數(shù)估計表明大鼠試驗前的基礎心律不齊次數(shù)是影響大鼠在實驗中是否發(fā)生心律不齊的因素，基礎心律不齊次數(shù)越高的大鼠在試驗中越有可能發(fā)生心律不齊(t=－∞，P＜0.001)。負二項部分參數(shù)估計可見，時間對心律不齊發(fā)生次數(shù)的影響有統(tǒng)計學意義(t=－4.12，P＜0.001)，隨檢測時間的延長心律不齊發(fā)生次數(shù)減少;與A藥相比，C藥的效應差別有統(tǒng)計學意義(C藥物:t=－2.94，P=0.0058)，即使用C藥的大鼠心律不齊發(fā)生次數(shù)較A藥少;試驗前基礎心律不齊次數(shù)越高的大鼠心律不齊發(fā)生次數(shù)也越多(t=3.25，P=0.0026)。

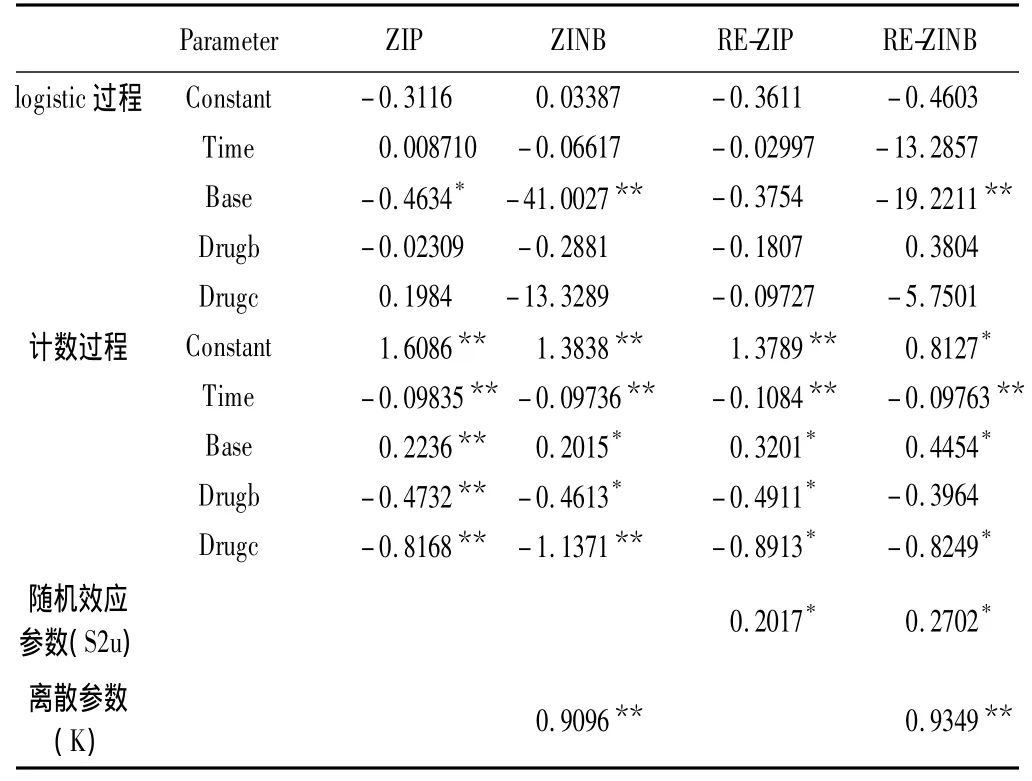
Parameter ZIP ZINB RE-ZIP RE-ZINB logistic過程 Constant －0．3116 0．03387 －0．3611 －0．4603 Time 0．008710 －0．06617 －0．02997 －13．2857 Base －0．4634* －41．0027＊＊ －0．3754 －19．2211＊＊Drugb －0．02309 －0．2881 －0．1807 0．3804 Drugc 0．1984 －13．3289 －0．09727 －5．7501計數(shù)過程 Constant 1．6086＊＊ 1．3838＊＊ 1．3789＊＊ 0．8127*Time －0．09835＊＊ －0．09736＊＊ －0．1084＊＊ －0．09763＊＊Base 0．2236＊＊ 0．2015* 0．3201* 0．4454*Drugb －0．4732＊＊ －0．4613* －0．4911* －0．3964 Drugc －0．8168＊＊ －1．1371＊＊ －0．8913* －0．8249*隨機效應參數(shù)(S2u)0．2017* 0．2702*離散參數(shù)(K) 0．9096＊＊ 0．9349＊＊

小 結

零膨脹計數(shù)模型將研究總體分成兩組不同的個體:一組中的個體根本不會發(fā)生相應的事件，另一組中的個體可能發(fā)生事件并假定服從負二項分布，將數(shù)據(jù)中的零看成“過多的零”和“真實的零”;但對重復測量或個體觀察值存在聚集性，同一個體間數(shù)據(jù)存在相關性時，即不滿足零膨脹獨立性的要求時，固定效應零膨脹模型的應用受到限制。本文將重復測量的個體看作隨機效應，建立隨機效應ZINB模型，不僅將固定效應ZINB模型擴展到能夠適合于重復測量數(shù)據(jù)，解決計數(shù)資料中零過多問題，也考慮了個體間隨機效應，能夠得到比FE-ZINB和RE-ZIP擬合更合理、精度更高的結果。

采用RE-ZINB模型分析藥物前期臨床試驗離體心臟心律不齊研究數(shù)據(jù)，結果表明大鼠的基礎心律不齊次數(shù)是大鼠藥物試驗中是否發(fā)生心律不齊的影響因素，提示初期是否有心律不齊，對用藥后結果有影響;試驗用C藥組大鼠心律不齊發(fā)生次數(shù)較用A藥組少，即試驗用C藥控制心律不齊發(fā)生次數(shù)效果優(yōu)于對照組(A藥);隨用藥時間延長，心律不齊發(fā)生的次數(shù)逐漸減少，但基礎心律不齊者減少發(fā)生的次數(shù)幅度較小。

本文只在計數(shù)過程引入了隨機效應，對于兩過程，即logistic過程和計數(shù)過程都引入隨機效應還需進一步研究。

1．Cohen AC．Estimation in mixture of discrete distributions．In Proceedings of the International Symposium on Discrete Distributions，Montreal，1963:373-378．

2．Johnson NL，Kotz S．Distributions in Statistics:Discrete Distributions．Houghton Mifflin，Boston，1969．

3．Lambert D．Zero-inflated poisson regression with an application to defects in manufacturing．Technometrics，1992，34:1-14．

4．Greene W．Accounting for excess zeros and sample selection in Poisson and negative binomial regression models．Working Paper No．EC-94-10，Department of Economics，Stern School of Business，New York University，1994．

5．Greene WH．Econometric Analysis，Upper Saddle River，NJ:Prentice Hall，2000．

6．Long JS．Regression Models for Categorical and Limited Dependent Variables．Thousand Oaks:Sage Publications，Inc，1997．

7．van den Broek J．A score test for zero inflation in a Poisson distribution．Biometrics，1995，51:738-743．

8．SAS/ETS 9．2:User's Guide．2008，SASInstitute Inc．，Cary，NC，USA．

9．Cameron AC，Trivedi PK．Regression Analysis of Count Data，Cambridge:Cambridge University Press，1998．