基于擬貝葉斯方法的二項分布總體率的區間估計

安金兵 李 勇

基于二項分布B(n，p)的總體率p的區間估計在生物醫學領域有比較廣泛的應用，其中很常見的就是Wald區間估計，不過Wald區間估計在覆蓋率及穩定性等方面存在比較明顯的缺陷〔1，2〕。Agresti等人〔3，4〕給出了與Wald區間估計形式上比較類似的估計方法;而以精確概率為基礎的區間估計〔5，6〕以及貝葉斯區間估計〔7〕在實際中也有很多應用。本文基本上沿用貝葉斯統計的思想，通過一種基于Kolmogrov分布距離的擬貝葉斯方法給出了總體率p的一種新的顯式解。

原理和方法

傳統的貝葉斯方法基于似然函數而構造，但是似然函數容易受到異常值和模型偏差的影響，因此一個比較常用的方法就是用一個對異常取值和模型偏差不敏感的函數代替似然函數構造擬貝葉斯后驗分布，進而進行統計分析而獲得穩健的性質。假設總體X的分布函數為F(t;p)，p∈Θ為未知參數，通過隨機抽樣得到的容量為n的樣本所對應的經驗分布函數為G(t)，則我們可以定義G(t)與F(t;p)之間的Kolmogrov分布距離d(p)以及如下的一個關于參數p函數K(p):

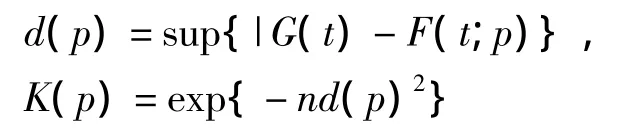
由于Kolmogrov距離d(p)在參數p為真實值時會隨樣本量的增大而趨于0，因而函數K(p)在參數p為真實值時取較大的數值，反之則取較小的數值，這種性質與似然函數非常類似。那么，如果參數p的先驗分布密度為 π(p)，則類似于 Lazar〔8〕、Greco〔9〕等人介紹的方法，利用函數K(p)代替似然函數，就可以將貝葉斯后驗分布修正為如下的擬貝葉斯形式:

進而利用上述擬貝葉斯公式就可以對參數p進行點估計或者區間估計。

假設總體X服從二項分布B(n，p)，參數p∈Θ=(0，1)，通過隨機抽樣得到總體X的一個觀測x。區別于以往的方法，本文并不是從B(n，p)分布的樣本觀測x的分布出發考慮問題，而是將總體率p看作是兩點分布B(1，p)的參數，同時將二項分布B(n，p)的觀測x看作是一個服從兩點分布B(1，p)的取值為0，1的樣本序列:y=(y1，…，yn)的總和。

然后，注意到以p為參數的兩點分布B(1，p)的分布函數F(t;p)與樣本序列y對應的經驗分布函數G(t)均為(0，1)上的階梯函數，并且除去界值0，1之外分別只有一個躍度p和^p=x/n，則經過計算得到:對于任意給定的p∈(0，1)，F(t;p)與 G(t)之間的Kolmogrov分布距離的數值恰好為p－^p。這樣，只要給定總體率p的先驗分布π(p)，則對于給定的置信水平α，就可以按照上述后驗分布密度π(p|x)給出參數p的區間估計［L(x)，U(x)］。

本文選擇參數p的先驗分布為均勻分布U(0，1)，即π(p)=1，則對于二項分布B(n，p)的一個實際觀測x，其樣本頻率為 ^p=x/n，利用上述基于Kolmogrov分布距離的擬貝葉斯公式，參數p定義在參數空間Θ=(0，1)上的后驗分布密度π(p|x)就是一個以x/n為最高點的單峰分布。若給定置信水平α，令:β=α/2，則置信下限L(x)可以通過下式確定:

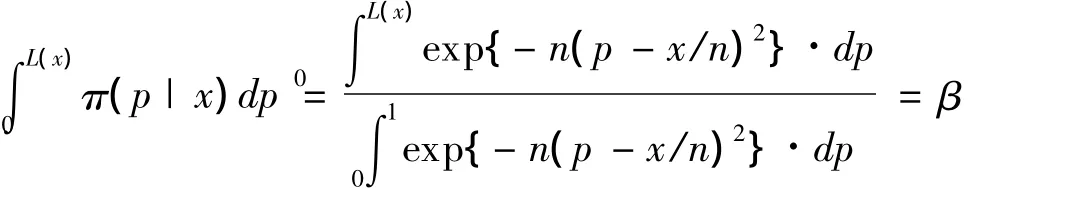
模擬研究

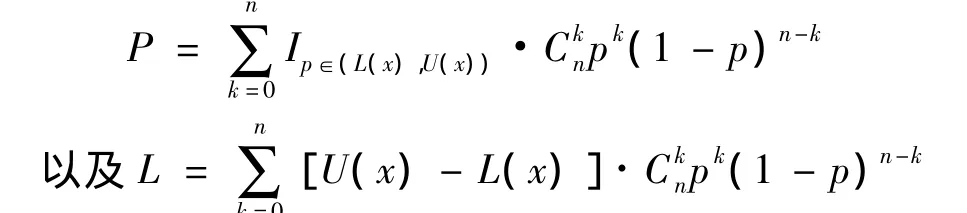
本文利用隨機模擬的方法對總體率p的Wald區間估計和本文基于擬貝葉斯方法所得的區間估計進行比較，本文選擇區間估計的覆蓋率和平均置信長度來評價區間估計的優劣。假設從二項分布B(n，p)中獲得一個觀測x，如果按照某種方法給出p的一個置信水平為 α 的區間估計［L(x)，U(x)］，則［L(x)，U(x)］對應的覆蓋率P及平均長度L分別為:在下面的部分，我們給定置信水平α=0.05，樣本量則分別選擇25、50和100三種情形，再從均勻分布U(0，1)中隨機獲取100個數作為總體率p的取值。對于每一個p，本文分別計算了Wald區間估計和擬貝葉斯區間估計的覆蓋率和平均區間長度并進行比較。模擬結果見圖1。分別用虛線及實線表示上述兩種區間估計的覆蓋率和平均置信長度。其中，上面的三個圖給出覆蓋率的相關結果，而下面的三個圖則給出平均置信長度的相關結果。為了清楚起見，在覆蓋率的幾個子圖中均加了一條取值為0.95的水平線以便觀察每種區間估計的覆蓋率與置信度的差別。

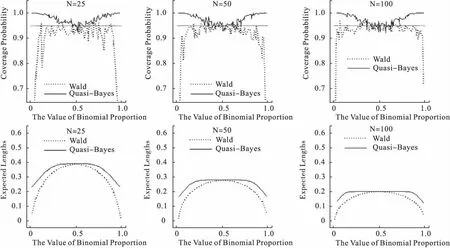
圖1 不同樣本量下Wald區間估計和擬貝葉斯區間估計的覆蓋率和平均置信長度

由圖1可以看出，Wald區間估計的平均區間寬度較小，而擬貝葉斯區間估計的平均區間寬度則稍大一點;Wald區間估計在很多情形下根本未達到0.95的覆蓋率，而擬貝葉斯區間估計的覆蓋率則幾乎總在0.95水平線之上，高于Wald區間估計的覆蓋率。值得注意的是，Wald區間估計的穩定性比較差，在參數空間Θ=(0，1)上有比較大的振蕩，并且比較容易受到總體率p的極端取值的影響，而擬貝葉斯區間估計的穩定性則比較好。所以，本文介紹的基于擬貝葉斯方法所得的區間估計對極端取值的穩健性較好。

討 論

首先，本文將樣本頻率 ^p=x/n與來自B(1，p)的樣本y對應的經驗分布函數G(t)聯系起來，再基于G(t)及某個參數p對應的分布函數F(t;p)的Kolmogrov分布距離d(p)構造了一個關于參數p的函數K(p)，并代替似然函數構造擬貝葉斯后驗分布，進而給出參數p的區間估計的一個顯式解。函數K(p)以分布函數為基礎進行定義，因而不容易受到模型偏差以及異常觀測的影響，而且隨機模擬的結果表明:當參數p在參數空間Θ=(0，1)上取值時，尤其當p接近0，1時，擬貝葉斯區間估計的覆蓋率比較高。事實上，生物醫學中很多有意義的數值例如治愈率、死亡率等常常在0，1附近取值，因此本方法存在實際的價值。

其次，根據擬貝葉斯后驗分布π(p|x)的表達，函數K(p)與似然函數有著類似的功能，因而擬貝葉斯公式不但能代替傳統的貝葉斯公式完成類似的功能，而且在一定程度上滿足穩健性。此外，根據擬貝葉斯公式的構造，函數K(p)還可以根據實際情況選擇其他形式。

最后，由于二項分布的總體率p的后驗分布是一個顯式表達，因此該方法很容易擴展到多個總體率的函數的估計問題，例如兩個總體率的差值、比值等的區間估計以及診斷試驗的ROC曲線估計等，這也是我們將來需要探討的問題。措施。包括對患兒進行積極的隔離治療，加強重點人群和重點地區的疫情主動搜索，開展行之有效的健康教育宣傳，加強醫療機構和托幼機構相關人員的業務培訓，加強托幼機構的晨午檢制度和消毒制度，通過村醫加大對散居兒童的監測和管理等，取得了較好的防控效果，使手足口病發病在4月份出現高峰后開始下降。

手足口病的人群分布與其他一些地區報道的情況基本相似〔4，5〕，男性發病高于女性，可能與男孩喜好活動，相互接觸密切有關。3歲以下兒童發病率高，主要原因可能為該年齡組兒童抵抗力低，家庭、社區中隱性感染者為本病的重要傳染源，散居兒童居家治療隔離不規范。

聚集性病例中83.6%發生在托幼機構，提示托幼機構為本病的重點防控單位。通過對疫情的處理，認為只要采取有效的措施即可控制手足口病的發病和流行。處理過程中除對患兒進行嚴格的隔離治療外，還對幼兒園進行徹底的消毒(活動室和教室開窗通風，被褥置于陽光下暴曬，餐具一用一消，玩具、教具規范消毒)，并嚴格落實晨午檢制度，發現疑似病例及時隔離，嚴禁病例帶病上課，同時利用專家現場講座、張貼宣傳畫、發放手足口病明白紙進行健康宣教，提高幼兒及家長對手足口病的認識，掌握預防知識，取得了較好的防控效果。

綜上述結果分析，手足口病雖然傳播途徑多、傳染性強、隱性感染者多又無疫苗、藥物等特異性防控手段，但只要嚴格病例隔離制度、重點地區消毒制度、托幼機構晨午檢制度、重點人群和重點地區的疫情主動搜索制度，同時做好手足口病的防治知識宣傳，提高群眾的防病意識和能力就能取得良好的防控效果。

1．呂冬梅，刑秀暖．46例手足口病發病情況分析．河北醫科大學學報，2008，29(5):755-756．

2．周永運，武桂珍．加強疾病監測與動態進行人類腸道病毒71型生物風險評估．中華預防醫學雜志，2009，43:328-330．

3．衛生部．手足口病預防控制指南(2009 版)．2009．6．4．http://www．moh．gov．cn．

4．鄭惠貞，李劍森，康敏，等．廣東省手足口病確診病例發病及診療情況調查．華南預防醫學，2008，34(5):10-13．

5．項娜，于海柱，崔蘭梅．北京市房山區233例手足口病流行病學分析．中國學校衛生，2008，29(9):817-818．