改性BM I樹脂固化過程的溫度控制優化

李都寧, 聶玉峰, 劉運芳, 梁 濱, 蔡 力

(西北工業大學理學院,西安 710129)

樹脂膜熔滲(RFI)是一種高性能復合材料的低成本制造技術,尤其適合于制造大型的具有復雜形狀且帶有加強筋的構件,如航空制造領域中的整體機翼、加強肋、梁等。其原理是在樹脂膜上鋪放預制體,然后將其用真空袋封裝并放入熱壓罐中,當纖維預制件完全被浸漬后,繼續升溫使樹脂發生交聯反應,最終固化成型。樹脂的固化過程決定了制件的最終性能,而采用實驗的方法耗資巨大且效果不明顯。因此,對固化過程進行數值模擬實驗以及開展關于成型工藝的優化研究,可減少生產成本的投入,同時也能縮短產品的研制周期。

許多學者在RFI固化工藝數值模擬方面進行了研究,A.C.Loos等[1]提出二維的數學模型來模擬RFI工藝中的固化過程,并預測了樹脂溫度分布。T.Behzad等[2]采用有限元法對天然纖維復合材料固化成型過程進行了模擬。譚華等[3]對熱固性樹脂基的固化過程用有限元法進行了三維瞬態數值分析,并與實驗數據進行了比較,陳祥寶等[4]對樹脂基復合材料制造過程溫度的變化進行了模擬研究,并與實驗值進行了比較。研究表明,溫度控制對構件固化形變的產生有直接的影響[5],因此需要合理控制固化過程中的工藝溫度。N.Patelelis等[6]采用數值模擬方法對固化工藝進行了分析,并采用遺傳算法得出最優的固化溫度控制工藝。A.Mawardi等[7]采用單純形法和模擬退火算法對固化的溫度控制進行了優化。K.H.Lee等[8]通過改變升溫速率等方式,來減少夾層復合材料固化時產生的殘余應力。然而,許多研究僅針對固化動力學方程進行數值分析,而依據固化時構件內部各點溫度的動態特性進行優化的研究很少。

本研究首先采用有限元/有限差分法針對以改性雙馬來酰亞胺樹脂為基體的RFI工藝的固化過程進行了數值模擬,得到構件中樹脂溫度與固化度的分布切片圖。提出了衡量固化好壞的控制參數,建立了優化溫度控制的方法,在一定程度上避免了固化不均勻現象的產生。

2 固化過程的模型及其求解

2.1 熱傳導控制方程

假設樹脂在發生固化反應時已經完全浸漬到預制件中,并認為纖維和樹脂具有相同的溫度,故只需考慮熱傳導,可得如下能量方程：

其中T為復合材料的溫度,H﹒為化學反應的放熱速率,ρ為復合材料的等效密度,Cp為復合材料的等效熱容,kx,ky及kz分別為三個空間方向的熱傳導系數。參數ρ,Cp,kx,ky及kz可以由纖維體積分數根據混合率近似確定[9]。

由于模具在熱壓罐中進行加熱,不妨假設模具表面溫度恒定,相應的初邊值條件為

其中 ˉT是給定的固化控制溫度,T0為初始時刻的溫度。

2.2 固化動力學模型

對于樹脂固化動力學的描述,通常忽略反應物如何相互反應的細節,而采用唯象學模型來描述。本研究采用Kamal提出的自催化動力學模型：

其中K是與Arrhenius溫度相關的速率常數,α為固化度,m,n為反應級數。固化度可以通過差動掃描量熱法(DSC)所測數據加以分析后獲得。對于改性雙馬來酰亞胺型樹脂,可將K,m,n看作溫度的一次函數,對實驗數據進行線性擬合后,可得如下等效固化動力學方程[10]：

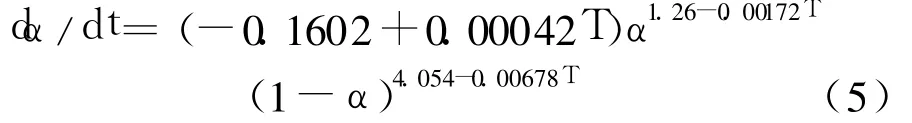
將樹脂固化放熱視為唯一的熱行為,則固化過程的放熱程度將與固化反應程度成正比,從而樹脂固化度可以表示為

2.3 控制方程離散

對方程(1)進行空間和時間上的離散,可建立相應的有限元/有限差分方程。將方程(1)中的時間微分項用向后差分法進行離散,得

其中Δt為時間步長,其中上標表示第n個時間步。再將方程(7)代入(1),并采用迦遼金加權余量法,便得方程(1)的有限元離散方程[9]：

類似地,對方程(6)兩端進行求導后,再利用向后差分離散可得

從方程(8)、(9)可以看出,溫度T和固化度α通過放熱率H﹒(t)耦合在一起。最終,通過聯立求解方程(8)、(9)便能動態模擬整個固化過程,其求解流程如圖 1所示。

圖1 溫度和固化度求解流程Fig.1 The flow chart of solving the temperature and the curing degree

2.4 溫度控制優化參數

為了對固化過程中的溫度控制進行優化,需要引入固化均勻度 ζ和溫差均勻度 τ來衡量固化質量的好壞,其定義如下：

其中,α為構件采樣點的固化度,ΔT為構件采樣點當前時刻與上一時刻的溫度差,顯然,ζ表示在同一時刻構件中固化度的最大值與最小值之差(極差),用于衡量固化的均勻程度;τ則表示在同一時刻構件中溫度變化的最大值與最小值之差,由于溫度的變化會引起熱應力,而不均勻的熱應力會產生構件的變形,從而 τ值可反映出溫差均勻度對構件形變的影響。從而,若 ζ,τ的值越小,則固化程度越均勻,且越不易產生翹曲變形。

3 模擬結果及分析

本研究對 U型構件[9,11]、飛機艙門構件的改性雙馬來酰亞胺樹脂RFI成型固化過程進行了數值模擬及對比分析,并對其固化的溫度控制進行了優化。

3.1 U型構件的模擬優化

A.Cheung以及Q.Zhu等[9,11]采用的幾何構件側面圖如圖 2所示。本文采用八節點六面體單元,將模型剖分為 792個節點,480個單元,固化所用的AS4/3501-6材料參數和固化動力學模型與文獻[9]一致,采用的固化溫度控制工藝為表 1中的 1 #。為優化溫度控制過程,在工藝初始溫度、最終固化溫度及溫度保持時間不變的前提條件下,模擬了不同情況下(見表1)固化均勻度ζ和溫差均勻度τ的變化(見圖3和圖4)。

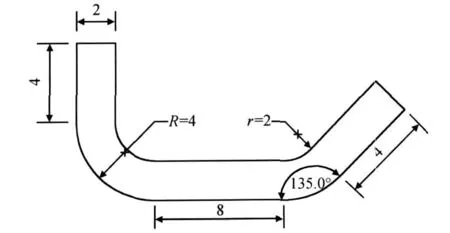
圖2 U型構件側視圖(單位cm)Fig.2 The dimensions of cross-section of U-shaped part(unit：cm)

表1 不同溫度控制工藝列表Tabel 1 The list ofdifferent temperature controls

圖3和圖 4分別表示在不同溫控情況下固化均勻度 ζ和溫差均勻度 τ的變化規律。在圖 3中,隨著保持溫度的升高,ζ的第二峰值會減小,第一峰值會增加。溫差均勻度 τ的峰值出現在溫度調控的時刻(圖4)。因此,在模擬出合適的保持溫度后,通過改變保持溫度開始和結束的時刻,可以模擬出 ζ和τ最大峰值均最小的溫度控制工藝,即4#(表1)。

圖5和圖6分別為在原溫度控制工藝(1#)和優化后的溫度控制工藝(4#)下固化度和溫度的對比圖。原控制工藝下得到的固化度和溫度曲線與文獻[9]中的結果相符合。優化溫度控制工藝后的結果(圖6),降低了溫度峰值,提高了前期的固化速率,進而縮短了總的固化時間。可見,文中使用的控制參數,即固化均勻度 ζ和溫差均勻度 τ,對于溫度控制過程的優化有顯著作用。

3.2 十字型構件的模擬優化

這里針對飛機艙門的三維十字肋構件模型(見圖 7)的固化過程進行了數值模擬,增強材料采用了G0814碳纖維平紋織物,纖維體積分數為 57%。加強筋的鋪層方式為,裁剪若干層20mm寬的織物,將其放置在兩層比底面寬兩個加強筋寬度的碳纖維布對折線處,用kevler纖維固定后,將包覆的纖維布打開,并用kevler纖維將其縫合在底面的碳纖維布上,保持加強筋位于中間。將另一條加強筋分成兩部分,采用同樣的方式分別縫合。對該構件用ANSYS進行網格剖分,得到 45680個節點,35856個單元。采用的BMI/G0814材料參數在表2中給出。

圖7 十字型構件示意圖(單位：m)Fig.7 Schematic diagram of the crossed part(unit：m)

實驗中采用的溫度控制工藝為表 3中的 1#。熱壓罐中的溫度與構件表面的溫度有一些差距,因此采用定溫邊界條件只是一種近似,要更精確的描述溫度邊界條件,還需要考慮熱壓罐中的熱對流,當溫度很高時還應考慮熱輻射[12]。由于 RFI工藝初期需要樹脂完成對預制件的浸漬,因此固化模擬將從樹脂在 130℃保持一個小時后開始,并取此時的固化度實驗數據作為初始固化度,而固化度可由DSC實驗進行測量分析得出。在圖8和圖 9中分別給出了固化進行 9700s后的溫度和固化度的切片圖。顯然最高溫度出現在構件底板與肋條相連的下部。這是因為樹脂發生交聯反應所釋放的熱量會累積在構件內,導致內部溫度高于表面。同時,構件內部的固化程度也高于表面。

表2 改性雙馬來酰亞胺型樹脂及纖維材料參數Tabel 2 Parameters ofmodified BMI resin and fibermaterial

表3 不同溫度控制工藝列表Tabel 3 The list ofdifferent temperature controls

圖8 9700s時的溫度分布Fig.8 The temperature distribution at 9700s

圖9 9700s時的固化度分布Fig.9 The curing degree distribution at 9700s

圖10將圖 7所示三處的溫度和固化工藝溫度進行了比較：初始時刻內部溫度已經高于模具表面溫度,隨著反應速率的逐漸減慢,在 453K時,內部溫度已經和表面溫度一致。此外,在初期以及溫度保持階段,A處的溫度高于 B、C兩處的溫度,這與溫度分布切片圖相吻合。圖 11是模擬出的固化度曲線與實驗值的比較。固化度實驗值是在同樣的工藝溫度下,通過對樹脂樣品的DSC分析所得的,可以看到模擬曲線與實驗結果基本吻合。

為得到優化的固化工藝過程,這里模擬了不同工藝下(表 3)固化均勻度ζ和溫差均勻度 τ的變化規律,詳見圖 12、圖 13。此時,固化均勻度 ζ僅有一個峰值,ζ的峰值隨著保持溫度的下降而降低。在圖13中,溫差均勻度τ的峰值與升溫速率有關,選擇保持溫度開始時間會改變升溫速率。若要使復合材料固化性能最佳,即使固化參數的最高峰值最小,則需選擇合適的保持溫度開始時間(2#)。因此,在選定合適的保持溫度后,再選擇保持溫度的開始時刻,可得到優化的溫度控制為3#(表3)。

圖12 不同條件下的變化曲線Fig.12 The variation curves of under different conditions

4 結論

圖13 不同條件下的變化曲線Fig.13 The variation curves of under different conditions

本研究對以改性雙馬來酰亞胺樹脂為基體的RFI固化過程進行了數值模擬。針對三維情況下的兩個典型構件,利用有限元/有限差分法模擬了成型工藝中溫度和固化度的分布情況及變化規律。提出了優化控制參數,獲得更加合理的固化溫度工藝。通過與實驗結果相比較,驗證本文方法的有效性。最終,為固化溫度工藝過程的優化設計提供一定的理論支持。

[1]LOOSA C,MACRAC JD.A process simulationmodel for themanufacture ofa blade-stiffened panelby the resin film in fusion process[J].Composites Science and Technology, 1996,56(3)：273-289.

[2]BEHZAD T,SAIN M.Finite elementmodeling of polymer curing in natural fiber reinforced composites[J].Composites Science and Technology,2007,67(7～8)：1666-1673.

[3]譚華,晏石林.熱固性樹脂基復合材料固化過程的三維數值模擬 [J].復合材料學報,2004,21(6)：167-172.

[4]陳祥寶,邢麗英,周正剛.樹脂基復合材料制造過程溫度變化模擬研究 [J].航空材料學報,2009,29(4)：61 -65.

[5]張紀奎,酈正能,關志東,等.熱固性樹脂基復合材料固化變形影響因素分析[J].復合材料學報,2009,26 (1)：179-184.

[6]PANTELELIS N,VROUVAKIS T,SPENTZAS K.Cure cycle design forcompositematerials using computer simulation and optimization tools[J].Forschung im Ingenieurwesen,2003,67(6)：254-262.

[7]MAWARDI A,PITCHUMANI R.Cure cycle design for thermosetting-matrix composites fabrication under uncertainty[J].Annals of Operations Research,2004,132(1～4)：19-45.

[8]LEE K H,LEE D G.Smart cure cycles for the adhesive jointof composite structures at cryogenic temperatures[J]. Composite Structures,2008,86(1-3)：37-44.

[9]CHEUNG A,POCHIRAJU Y Y K.Three-dimensional finite element simulation of curing of polymer composites [J].Finite Elements in Analysis and Design,2004,20 (4)：895-912.

[10]于佳,王振清,張博明,等.改性雙馬來酰亞胺樹脂固化工藝動力學模型的建立 [J].材料工程,2005, (4)：55-59.

[11]ZHU Q,PH ILIPPEG,LIM,CHARLES T.Dimensional accuracy of thermoset composites：simulation of p rocessinduced residual stresses[J].Journalof Composite Materials,2001,35(24)：2171-2205.

[12]胡照會,王榮國,馬李,等.CFRP壓力容器固化成型過程中邊界條件的確定 [J].纖維復合材料,2007, (1)：26-28.