基于Gardner算法的抗載波偏差的一種改進算法

楊帆，林平分

（北京工業大學嵌入式重點實驗室，北京100124）

在數字通信系統中，接收端設備為了保持采樣時鐘與接收到的信號互相同步，必須計算采樣時間與信號上的最佳采樣點之間的時間差，即采樣時鐘偏差τ，并且跟蹤這個τ，使得τ保持在足夠小的范圍內。TED（Timing Error Detector）就是計算采樣時鐘偏差τ的模塊。TED模塊只負責計算出這個采樣時鐘偏差τ，然后由PLL等模塊負責把該時鐘偏差糾正過來，從而實現發送和接收的同步采樣。

Gardner算法[1]是數字通信接受端上被廣泛使用的一種TED（Timing Error Detector）算法，它擁有實現簡單、硬件消耗較小、精確度高、對相位偏差不敏感的特點。但是這個算法的可行性有一定的前提：即假設每個采樣值的相位偏差不變，也就是說沒有載波偏差。當假設條件不滿足時，算法的性能將會受到影響，可能無法達到系統的性能要求。為了解決這個問題，本文提出了一種基于Gardner算法的改進算法，該算法可以在載波偏差存在的情況下工作，并且表現出接近無載波偏差時的性能，提高了原算法的可靠性和準確度。此外還對改進的算法進行了仿真和驗證，并列出了仿真結果，仿真結果證明改進后的算法在載波偏差處于一定范圍時，可以提高原算法的精確度30%~93%。

1 原理描述與數學證明

Gardner算法在每個符號周期T內只需要采樣2次。改進算法只增加了一個計算模塊和一個乘法器，如圖1所示。

圖1 改進后的算法結構Fig.1The improved algorithm’sstructure

圖1中，{x（rT）}是采樣后的信號，如果{x（rT）}不帶有載波偏差，經過原Gardner算法模塊，輸出是{E（U（τ））}值，在采樣信號平均功率既定的條件下，{E（U（τ））}與τ滿足確定的對應關系，由這個關系函數可以計算出τ的值，再把τ輸出給糾正采樣時鐘偏差的模塊，完成糾正任務，同時TED會不斷重復計算{E（U（τ））}的值來跟蹤τ的變化。如果{x（rT）}帶有載波偏差，{E（U（τ））}與τ的對應關系改變。改變后的對應關系沒有使{E（U（τ））}失去計算出τ的能力，而是使得{E（U（τ））}計算出τ的精確度變差。精確度變差會影響TED跟蹤τ值的能力。為了在載波偏差存在的情況下得到較好的精確度，改進后的算法給采樣信號乘上一個輻角隨序列號r線性增加的函數，如圖1中的exp{j2πfarT}，這個乘法相當于給采樣信號做了一個跨度為fa的頻譜搬移。載波偏差的增加對Gardner算法精確度的影響不是線性增加的，也就是說并非載波偏差越大，對精確度的影響就越大。載波偏差的增加對Gardner算法的精確度的影響是周期變化的，后文會證明出這個周期是，所以當載波偏差是的倍數時，Gardner算法的精確度會表現得接近于沒有載波偏差，不需要計算出載波偏差本身，只需要計算出載波偏差與最臨近的的倍數的差值，再把采樣信號在頻域上搬移這個差值，這樣相當于把載波偏差搬移到對精確度影響最小的區間。這樣就使得在載波偏差存在的情況下，τ的計算擁有更好的精確度。

計算模塊的任務是由圖1中的{E（U（τ））}序列和τ序列計算出搬移距離fa的中間變量，乘法器的任務是把采樣信號做跨度為fa的搬移。

采樣之前的信號中，每一個符號所持續的時間T內有一個最佳采樣點，Gardner算法要求在每個預計的最佳采樣點上采樣，并且在每兩個最佳采樣點之間的時間段的正中央采樣，每個符號周期內采樣2次[2]。預計的最佳采樣點與真實的最佳采樣點之間的時間差即為采樣時鐘偏差τ。

用r代表符號序列，用{x1（rT）}和{xQ（rT）}來表示在第r個符號周期內最佳采樣點上的采樣

之間的時間段的正中央的采樣值。其中{x1（rT）}、{xQ（rT）}，（r∈N）即采樣得到的數字信號，將被TED以外的其他模塊所使用。據。Gardner算法的表達式是：

當采樣時鐘偏差為零，即τ=0時，有：

為了論述簡潔，不妨只針對路信號論述，

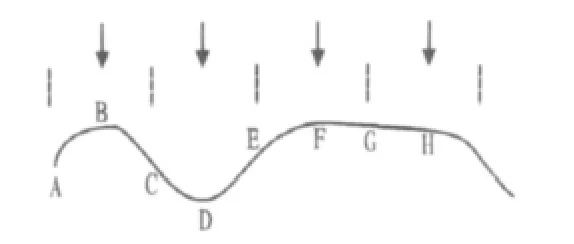
圖2 信號的采樣時間Fig.2Sample time on the signal

圖2摘自文獻[2]。圖2中黑色箭頭所指的位置：B點、D、F、H點表示最佳采樣點，即{x1（rT）}，（r∈N）；黑色豎線所指的位置：A、C、E、G點表號大小的單位時，不妨認為x1（B）=1，x1（D）=1，x1（F）=x1（H）=1，x1（A）=x1（C）=x1（E）=0顯然可得:

即在信號由1翻轉為-1、由-1翻轉為1、不翻轉這3種情況下{UIr（0）}的值都是0。這個結論也適用于{UIQ（0）}，即在τ=0的情況下有Ur（0）=UIr（0）+UQr（0）=0。在τ偏離0的時候，{Ur（0）}也偏離0，偏離大小隨翻轉情況不同而不同。由于信號翻轉情況的概率服從既定的分布率的[3]，{Ur（0）}的統計均值{E（Ur（0））}在τ偏離0時的值是可以確定的。Gardner的論文[1]中已經詳盡證明，在相位偏差不變、經過接收機濾波后的符號脈沖為偶函數、信號帶寬超過采樣頻率40~100%的條件下，

由于{E（Ur（0））}是統計均值，已經與具體的符號序列無關，所以略去腳標r。K是由采樣頻率、符號脈沖在頻域的形狀所決定的一個值[4-6]，在符號脈沖和采樣頻率確定時，K可以視為常量。所以得到{E（Ur（τ））}隨τ變化的函數圖形如圖3所示。

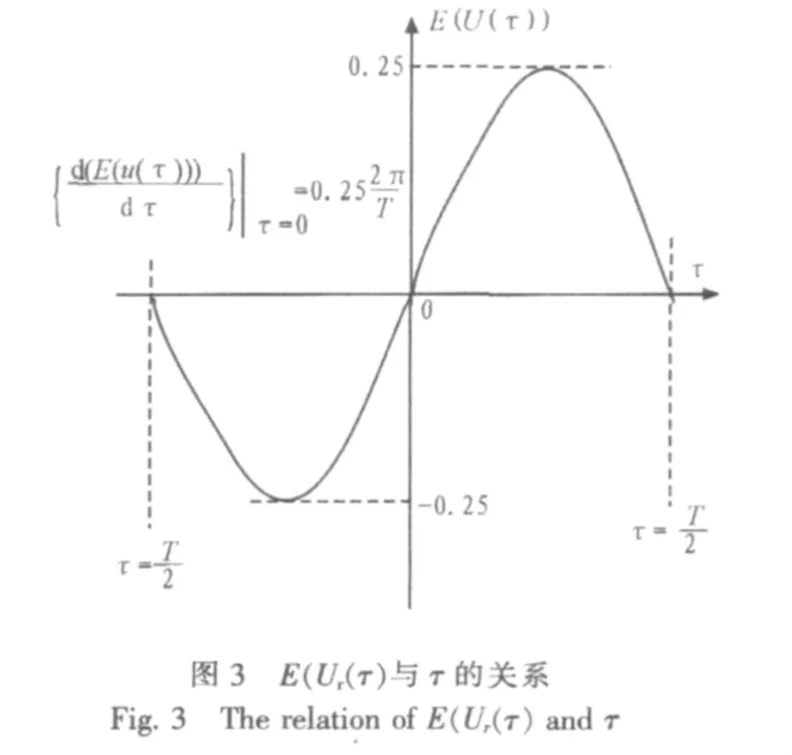
由于{E（Ur（τ））}顯然是周期為T的周期函數，圖3中只給最佳采樣點的采樣值的能量歸一化為1時，{E（U（τ））}函數圖形在τ=0處的斜率最大值0.25，最小值-0.25。{E（U（τ））}函數在τ=0處的導數代表了這個TED算法的精確度。因為TED模塊是用{E（U（τ））}的值來估計τ的值的，在信噪比一定的情況下，TED模塊可分辨{E（U（τ））}的值的精度就是一定的，設這個精度值是Δ{E（U（τ））}，確定Δ{E（U（τ））}的值在τ=0附近對應的Δτ也是確定的。TED模塊可以分辨的最小的Δτ可以這樣計算出來：

所以，信噪比一定的情況下，{E（U（τ））}函數在τ=0處的導數越大，TED模塊可分辨的最小值Δτ越小，精確度也就越好。

Gardner算法的成立條件大多是容易滿足的，只有假設相位偏差恒定這一條不容易滿足[7]。如果有載波偏差存在，相響，在載波偏差Δf與符號周期T之間滿足等近于0，Δτ趨近于無窮大，TED模塊的精確度也就趨近于無窮差。現在證明這一點：

設有載波偏差的信號y（t）=x（t）·exp（j2πΔft），x（t）此時為沒有載波偏差的理想信號，有

假設可以對x（t）進行直接采樣，令對x（t）進行直接采樣得到的Gardner算法表達式是Ur（τ）ideat。y（t）對采樣得到的Gardner算法表達式是Ur（τ）offset，有：

把式（9）代入式（10）中，合并同類項后得到：

其中H1、H2、H3和H4分別代表一個關于Δf和τ的三角函數：

運用三角公式，有：

對于H3和H4情況做同樣的推導，可得：

將式（14）代入式（11）可以得到：

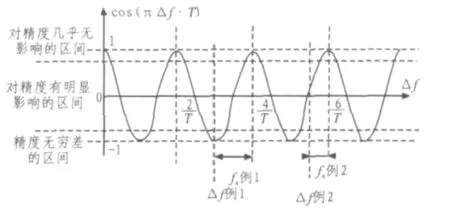
圖4 Δf對精度的周期影響Fig.4Δf’s periodical impact on the accuracy

對于解決這個問題，只需對有載波偏差的信號做一個跨度為fa的頻譜搬移，使得{fa+Δf}的值處于對TED精度幾乎沒有影響的區間上。fa的值可以在不求得Δf的情況下得到。因為cos（πΔf·T）的值可得，所以可以得的最大的整數，如圖4所示。cos（πΔ·fT）的值是由式（14）得到的。塊的工作原理并非一勞永逸地計算出一個不變τ的值，而是始終不斷地計算{E（Ur（τ））}的值來跟蹤τ值的變化[8]，所以TED會反復計算出τ=0附近的多個{E（Ur（τ））}的值，只需要把這些值存儲下在TED內，并不斷更新，就能計算出于在信號平均功率、采樣周期、脈沖形狀既定的情況據式（14），cos（πΔf·T）也可以得出，從而得出fa：

得到fa后只需用y（τ+rT）·exp（j2πfa·rT），（r∈N）和y（τ+可得到幾乎不受Δf影響的接近{E（Ur（τ）ideal）}的{E（Ur（τ））}值，從而在有載波偏差的情況下得到高精度的τ。

2 仿真結果

原算法和改進后的算法使用matlab7.0做了對比仿真，圖5中的左右兩個圖都是由仿真得到。圖5中縱軸是把接收信號采樣點的平均功率歸一化為1后，Gardner表達式的值，橫軸是用2 000個離散的時間代表一個周期τ內的連續時間。由結果可以清晰看到，改進后的算法可以對每一個Δf都能給出在τ=0附近有較大斜率的曲線，也就是說：對仿真中使用的每一個Δf的值，改進后的算法都不受影響，能給出接近理想的精度。仿真使用的是QPSK信號，符號函數使用的是滾降系數是0.5的升余弦函數，AWGN信道。圖5是輸入信號信噪比為30 dB的仿真結果。

圖5 對比仿真結果Fig.5Simulation results in contrast

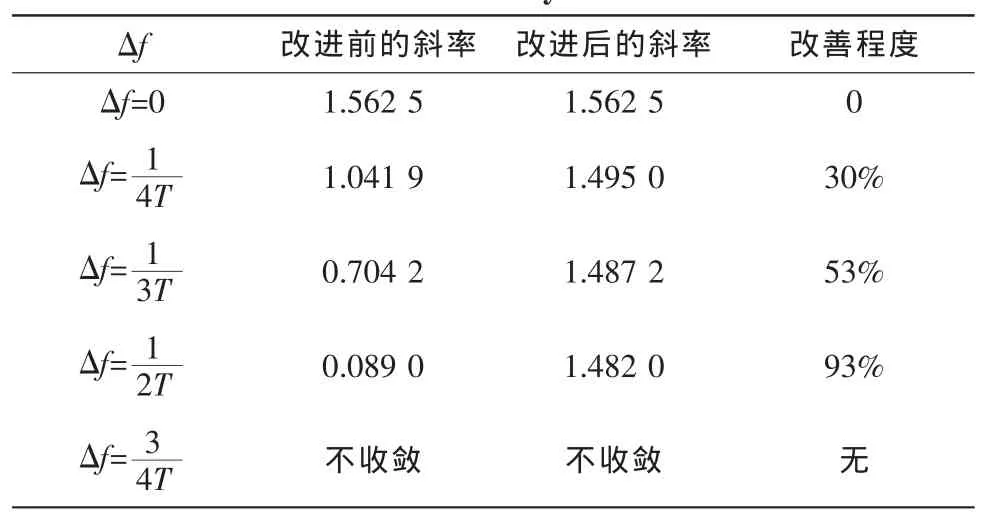
表1 改善前后精確度對比Tab.1Accuracy contrast

3 結論

本文提出了一種對數字通信中的TED模塊Gardner算法的改進，并給出了改進算法的數學證明和仿真結果。改進后的算法增強了Gardner算法可能對抗波偏差的性能，同時繼承了Gardner算法的實現簡單、硬件消耗較小、精確度高、對相位偏差不敏感的特點。同Gardner算法一樣，改進后的算法適用于BPSK、QPSK的帶限信號和AWGN信道，對QAM信號和嚴重的多徑信道表現欠佳。

[1]GARDNER F M.A BPSK/QPSK timing error detector for sampled receiver[J].IEEE Trans.On Comm，1986，34（5）:423-429.

[2]PELET E R，SALT J E.On economical timing-error detectors for QAM receivers[J].IET Communications，2007，1（4）:618-622.

[3]LOU Huang.A new lock detector for Gardner’s timing recoverymethod[J].IEEETransactionsonConsumer Electronics，2008，54（2）:349-352.

[4]GAPPMAIR W.Self-noise performance of zero-crossing and Gardnersynchronisersappliedtoone/two-dimensional modulation schemes[J].Electronics Letters，2004，40（16）:1010-1011.

[5]GAPPMAIR W，Cioni S，Corazza G E，et al.Symbol-timing recovery with modified Gardner detectors[C]//International Symposium on Wireless Communication Systems，Siena:[s.n.]，2005：831-834.

[6]MAHLOUJI M，DANESFAHANI R.An investigation into timing synchronization of pi4-DQPSK signals using Gardner symbol timing error detectionalgorithmandpolyphase filterbanks[C]//Information and Communication Technology，Damascus:[s.n.]，2006：2274-2278.

[7]LOU Huang.Timing recovery methods for VSB receivers[J].IEEE Transactions on Consumer Electronics，2007，53（2）:310-312.

[8]GONG Feng-kui，GE Jian-hua，QIAN Feng.Symbol timing recovery algorithm with near timing-jitter free for ATSC DTV receivers[J].IEEE Transactions on Consumer Electronics，2007，53（2）:313-318.