明渠水聲信號測速方法研究

王 婧，劉紀元 ，焦學峰，張 皓

（1.沈陽航空航天大學 電子信息工程學院，遼寧 沈陽 110136；2.中國科學院聲學研究所綜合聲納實驗室 北京 100080；3.北京航瑞博泰科技有限公司 北京 100102）

在注重節省能源，提高經濟效益和產品質量的今天，流量計量與測試的重要更加突出并為越來越多的人所認識。特別是隨著現代工業生產的飛速發展，人們對流量測量的要求越來越高，對流量測量技術和儀表的研究和開發不斷深入，流量測量方法儀表的種類也越來越多。在一些大型引水場合，如：城市供水引水渠，火電廠引水和排水渠，污水治理流入和排放渠，工礦企業水排放以及水利工程和農業灌溉用渠道，明渠流量計發揮極其重要的作用。而超聲波明渠流量計中影響流量的一個重要因素就是水速的測量及其精度，因此合理獲取精確的水流速顯得至關重要。

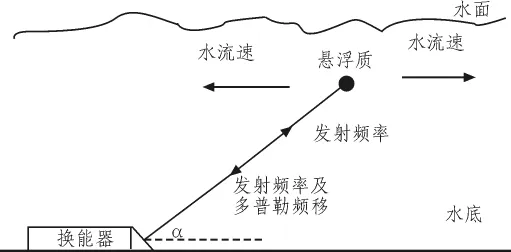
圖1 多普勒原理圖Fig.1 Doppler schematic

1 水聲測速的基本原理

水聲測速的原理圖如圖1所示。

在換能器收發共置的情況下，聲波經發射后，測量聲波被水中移動的懸浮物質反射，此時回波信號與發射信號就會產生頻率差，即多普勒頻移，利用頻移就可以計算流速。

在一個測量周期內，首先換能器以發射頻率fc發射一束超聲波，這束波被一個懸浮質以與發射頻率不同的頻率接收到（或反射），這一過程就產生了多普勒頻移，然后波束又一次反射回換能器，再一次產生一個多普勒頻移。兩個多普勒頻移存在于這個交換過程中，前一個是信號通過換能器傳到懸浮質，第二個是信號從懸浮質反射回換能器。

應用多普勒原理，同時考慮發射角α可以推導以下結論：

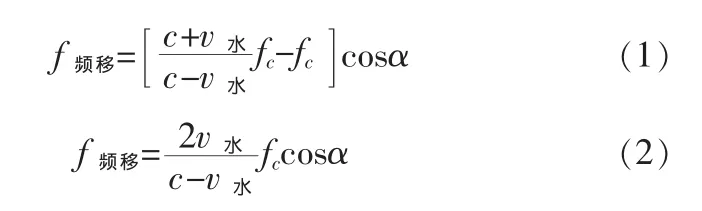
式中，c為聲波在水中的傳播速度，常溫下大約1 500 m/s；v水為水流流速；fc為聲源發射信號頻率；α為發射信號與水平面的夾角。

在測量的過程中，由于v水＜＜c，公式簡化為：

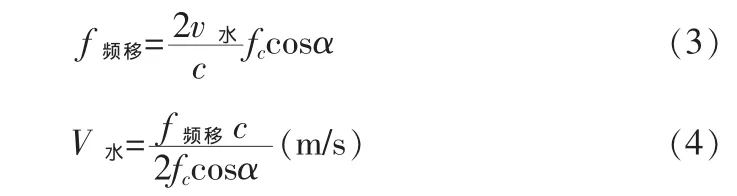
因此，要計算多普勒頻移，只要將所接收到的回波做FFT后與水靜止時的FFT做差，就可以得到頻移f頻移，從而得到水的流速V水。

2 三種方法概述

2.1 疊加法

顧名思義，疊加法就是取多次回波頻譜將其相加，這樣做的好處是，經過多次疊加，一些隨機噪聲的幅值隨著疊加次數的增多增長很緩慢，但信號的頻譜卻增長明顯，因此信號越來越突出，而噪聲信號則越來越不明顯了[1]，證明如下。

設每次測得頻率為fi，每次測量值是互相獨立的隨機量，設其方δ2差均為，進行N次獨立測量后的樣本均值為

方差為

可見疊加的次數越多，效果越好，但是為能夠反映當前水速值，測量時間不宜過長（次數不宜太多）。

2.2 譜減法

與語音信號的“譜減法”[2]不同的是，“回波譜減法”不是減去“寂靜段”的噪聲功率譜，而是帶信號去噪。步驟如下：

1）首先發射換能器不發射信號，觀察回波頻譜，確定干擾的大概范圍R。

2）調整水流速，使其對應的頻譜在R之外，保存R內的數值。本步驟執行多次。

3）根據上一步驟整理數值，看干擾R內的數值與主頻值的比例關系及主頻與真實多普勒頻率值的關系。

4）在接收的回波信號中依據比例減去干擾。

2.3 全相位頻譜校正法

通過式（4）可以看出，水速的獲得是通過回波的頻率獲得的，要想提高測速的精確度，就要知道回波的精確頻率。如果真正的頻率在兩根譜線之間，則誤差最大，為半個頻率分辨率[3]。因此頻譜校正對于提高測量精度是很必要的。傳統FFT結果可以通過一些算法實現頻譜校正，如能量重心法、比值法等。但以上的頻率估計都是在傳統的FFT架構下進行的，因而傳統FFT固有的頻譜泄露效應無疑會在很大程度上影響這些校正法的精度。全相位FFT算法（apFFT）具有初始相位不變和有效防止頻譜泄露的特性[4]。

在圖 2 中，ω*代表信號的數字角頻率，k*=[ω*/Δω]（“[]”代表四舍五入），Δω 是角頻率分辨率ω^*，A^，及θ^0為校正后的角頻率、幅值及相位。

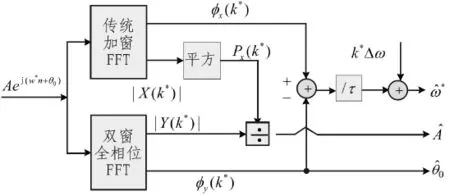
圖2 FFT/apFFT綜合相位差法的頻譜校正流程Fig.2 The spectra calibrating process of FFT/apFFT method

由圖2可以看出，FFT/apFFT綜合相位差法需要對序列進行2次譜分析，一次傳統FFT分析，一次全相位FFT譜分析。雙窗全相位FFT過程，即對數據進行全相位預處理，然后進行傳統的FFT運算。過程如下：

1）構成一個N點的漢寧窗；

2）漢寧窗對自己求卷積，得到2N－1點的卷積窗；

3）求2N－1點的卷積窗的和；

4）將卷積窗的每一項除以卷積窗的和，得到2N－1點的歸一化卷積窗；

5）將數據的1到2N－1項和歸一化卷積窗相乘，得到加窗的2N－1項；

6）將第 1項和 N+1項，第 2項和 N+2項 ...第 N－1項和第2N－1項相加，得到經過全相預處理的N點序列；

7）對6）中的經過全相位處理的N點序列做FFT運算；

以下簡單介紹FFT/apFFT。

已知單頻復指數信號為

信號的數字頻率ω*表示為β倍頻率間隔2π/N的形式（β可以是小數）。

其歸一化的FFTapFFT譜：

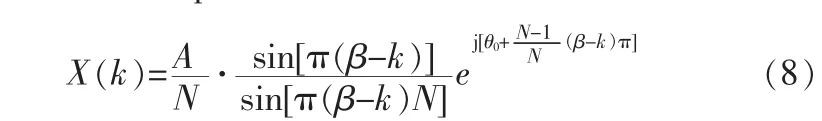
其歸一化的apFFT譜：

FFT/apFFT校正法需要2N－1個樣點。對后N點作FFT，對全部的2N－1點作apFFT。對頻率值β取整或從振幅譜可確定譜峰位置位于 k0=[β]處，[]表示取整，ang（.）表示取相操作。

由式（9）可知，在k0的apFFT的初始相位值φ0，則相位校正值：

由式（8）和（9）可知，在k0的FFT的相位值減去apFFT的相位值可得校正后的頻率值β：

由式（7）和（8）可知，在的FFT的振幅值平方除以apFFT振幅即得校正后的振幅A:

3 結果分析

3.1 未加任何處理的回波波形

圖3為未加任何處理的靜水中的回波信號頻譜圖。

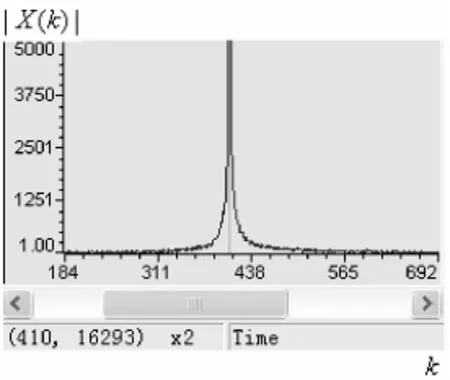
圖3 靜水中的回波信號頻譜圖Fig.3 Echo signal spectrum of still water

經過采樣后的回波信號的余頻所在的譜線數在409.6≈410根處。

圖3以及下面的圖4、圖5、圖6的橫軸代表的是譜線根數，單位為頻率分辨率，即fs/N Hz，N為FFT點數。縱軸是對采集到的數字信號做FFT后取絕對值。單位為10/216V。

在上圖的回波波形中可以看出，回波有噪聲干擾。

3.2 疊加后的頻譜圖

疊加后的靜水及水流動的回波頻譜圖如圖4所示。

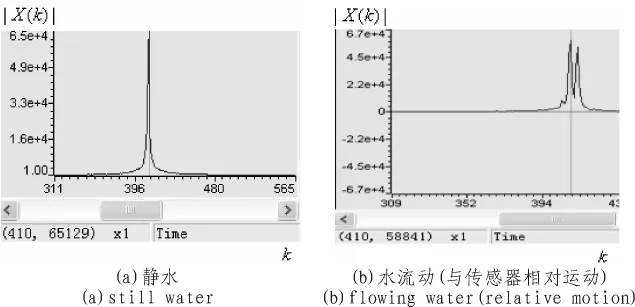
圖4 疊加后的靜水及水流動的回波頻譜圖Fig.4 Superposed echo spectrum of still water and flowing water

由上圖可以看出，疊加后的頻譜圖輪廓清晰，峰值明顯，噪聲與信號的頻譜比較，微乎其微。但是此時的主頻處410根譜線的峰值仍然大于真實譜線處的峰值 （410根右側的那個峰值）。

3.3 疊加+譜減法后的頻譜圖

圖5為靜水中疊加及譜減法后的回波頻譜圖。

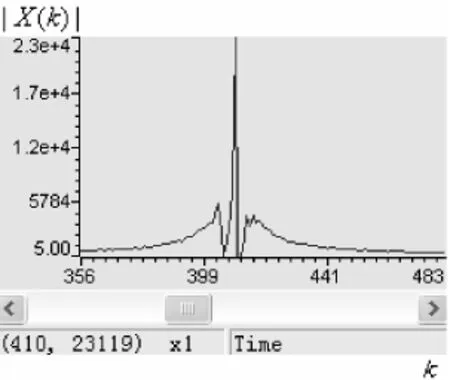
圖5 靜水中疊加及譜減法后的回波頻譜圖Fig.5 Echo spectrum after superposition and spectral subtraction of still water

從圖6中可以看到，頻譜圖稍亂一些，這是由于系數選取的緣故，因為所選取的系數是多次測量取的平均值。但是回波的波形不是固定不變的，所以經過處理后的頻譜圖為當前的狀態，但是這不會影響判斷結果。

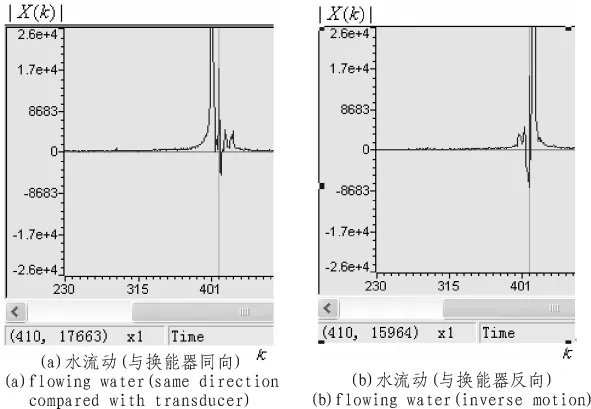
圖6 水流動疊加及譜減法后的回波頻譜圖Fig.6 Echo spectrum after superposition and spectral subtraction of flowing water

現在已經可以看出主頻處410根譜線的峰值不再大于真實值譜線處的峰值了。當測量真實結果在R譜線范圍內，譜減法后的頻譜也不會影響真實值的判斷。因此此種辦法有一定效果[6-7]。

3.4 FFT/apFFT校正前后對比

發射的信號頻率為：1 MHz；信號幅值：0.8 V；初相：180；采樣頻率：25.51 kHz；FFT/apFFT分析校正后的頻譜如圖7所示，表1列出了校正前后數據（靜水）。

在圖7中，橫坐標k表示的是譜線根數，單位為頻率分辨率，即fs/N Hz，N為FFT點數。縱坐標y1表示的是加窗后的FFT振幅譜，單位為V；y2表示的是振幅譜，單位為V；y3代表的是apFFT的相位譜，單位為（°）；y4表示的是歸一化的相位偏離校正值，單位為Δf Hz，Δf代表頻率分辨率；y5表示的是振幅校正值，單位為V[8-9]。

注意這里是欠采樣，所以回波頻率指的都是余頻。為了考核此種方法的可行性及穩定性，在常溫下做了多組實驗來驗證。調節水速從而使回波產生不同的頻率，通過綜合應用方法對回波頻率進行校正（噪聲的幅值大約是信號幅值的0.1倍）。整理后的結果如表2所示。其中公式（4）中 α 的取 30°。

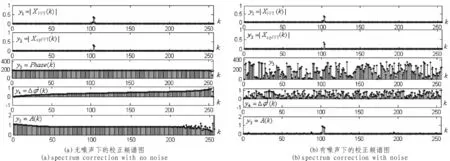
圖7 FFT/apFFT頻譜校正Fig.7 FFT/apFFTspectrum correction

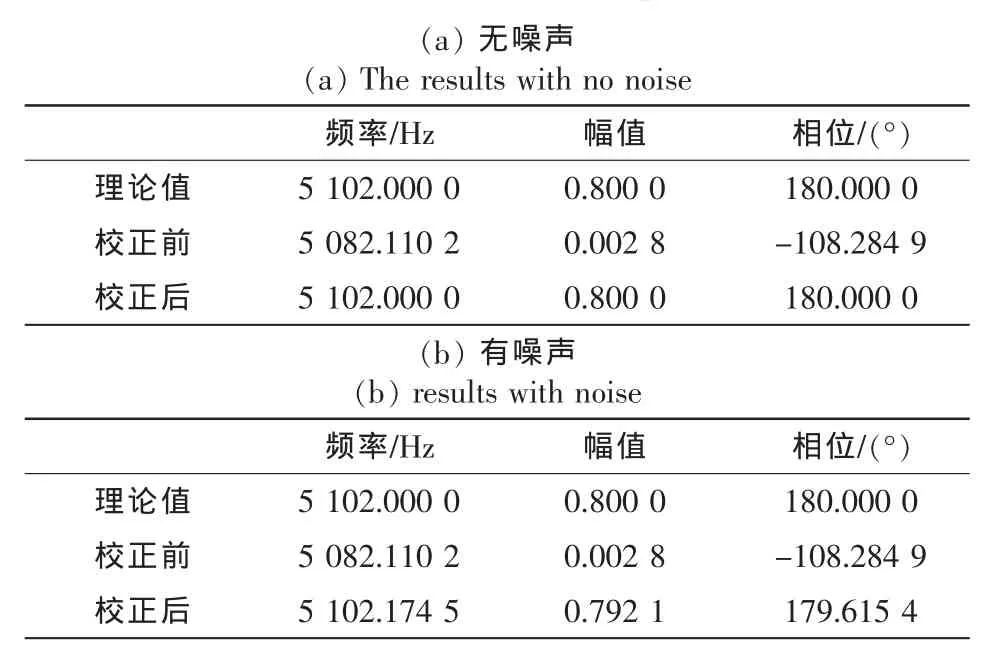
表1 FFT/apFFT頻譜校正結果前后數值Tab.1 Results before and after FFT/apFFT correction

由于測速關心的主要問題是回波的頻率，故表2里只對頻率的校正前后做了對比。此處，相對誤差=（測量值-理論理）/理論值。

由式（4）可知，多普勒頻移的相對誤差就是水速的相對誤差。因此在計算水速的相對誤差時，可以通過計算多普勒頻移的相對誤差來獲得水速的相對誤差，減少計算量。

以第1組數據為例：

f頻移=5 159.735-5 102=57.735 Hz

由表中的數據可以看出，在有噪聲的情況下，校正后的相對誤差比校正前的相對誤差減低了很多，相對誤差基本降低了一個數量級。此方法在水速測量上對提高測度精度是起到了一定的作用。

表2 FFT/apFFT頻譜校正方法測試數據Tab.2 Test data of FFT/apFFT correction

4 結 論

本文在設計中將“疊加法”、“譜減法”及“全相位頻譜校正法”結合應用于水速測量中。這些處理方法的結合，一方面可以降低噪聲干擾，突出信號，另一方面降低了主頻對其他頻率的干擾。特別是全相位頻譜校正方法的引用，可以避免

離散頻譜引起的誤差，能夠在有噪聲的情況下，將誤差降低一個數量級。

[1] 高晉占.微弱信號檢測[M].北京:清華大學出版社，2002.

[2] 楊行峻，遲惠生.語音信號數字處理[M].北京:電子工業出版社，1995.

[3] 丁康，謝明，楊志堅.頻譜分析校正理論與技術[M].北京:科學出版社，2008.

[4]王兆華，黃翔東.數字信號全相位頻譜分析與濾波技術[M].北京:電子工業出版社，2009.

[5] 黃翔東，王兆華.基于全相位頻譜分析的相位差頻譜校正法[J].電子與信息學報，2008，30（2）：293-297.HANG Xiang-dong，WANG Zhao-hua.Phasedifference correcting spectrum method based on all-phase spectrum analysis[J].Journal of Electronics&Information Technology，2008，30（2）:293-297.

[6] 李啟虎.聲納信號處理引論[M].北京:海洋出版社，1985.

[7] 俞小鼎.多普勒天氣雷達原理與業務應用[M].北京:氣象出版社，2006.

[8] 張賢達.現代信號處理[M].北京：清華大學出版社，2002.

[9] 劉波，文忠，等.MATLAB信號處理[M].北京：電子工業出版社，2006.