離散頻譜梯形窗幅度比值校正法的頻率估計

朱 磊，董 亮，孫振龍，劉樹東

（齊齊哈爾大學 a.通信與電子工程學院；b.招生辦，黑龍江 齊齊哈爾 161006）

0 引言

正弦信號的頻率估計是信號處理領域中的一個非常重要的問題，而FFT算法的提出可快速有效地實現正弦信號的頻率估計問題，但是由于FFT的頻譜泄露和柵欄效應，使得直接由FFT來估計信號的頻率效果不是很理想，因此必須進行頻譜校正。1975年，John C.Burges采用插值法對加矩形窗的離散頻譜進行校正[1]。1983年，Thomas Grandke提出了加漢明窗的內插校正法[2]。國內一些學者也提出了許多離散頻譜的校正方法：如相似最大似然頻率估計法[3]、比值法[4-8]、相位差法[9-10]、能量重心法[11]、FFT+DFT細化法等等。這些方法實現過程復雜，計算量大，不易于滿足DSP的實時信號處理，特別在有噪聲時，估計性能明顯下降。

針對上述情況，筆者提出了一種離散頻譜梯形窗幅度比值校正法。通過分析梯形窗函數的信號模型了解到，通過選取適當的兩邊傾斜度，可以獲得較好的幅頻特性。因此，本文在分析梯形窗時域、頻域特性的基礎上，利用離散頻譜中最高譜線和次高譜線兩條譜線的幅度比值關系，推導了加梯形窗的幅度比值頻譜校正公式，采用仿真數據對該算法的頻率校正精度進行了分析，并與加矩形窗時的頻譜校正精度進行了比較，誤差分析和實驗結果表明該算法在信噪比較低時，估計精度高，性能明顯優于加矩形窗的情況。

1 梯形窗函數模型

梯形窗函數的時域波形如圖1所示。具體函數形式為

相應的幅值譜為圖2所示，具體的表達式為

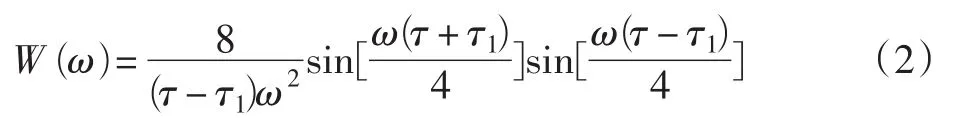
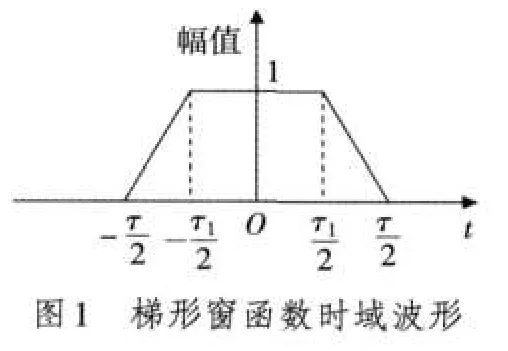
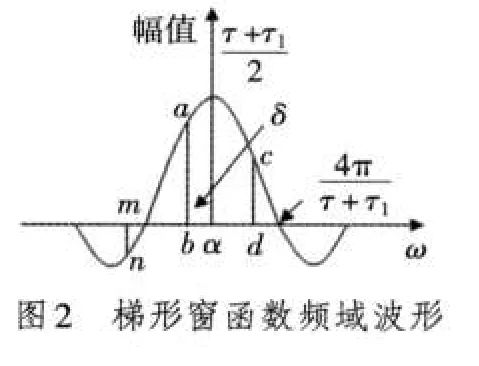
由圖可見，梯形窗的主瓣寬度比較寬，絕對值最小的兩個零點之間的距離為8π/τ+τ1，但是旁瓣電平比較低。表1為幾個常見的窗函數幅頻特性對比表，由表1可以知道，梯形窗函數是一種性能較好的窗函數，其幅頻特性的主瓣寬度雖然比矩形窗函數幅頻特性的主瓣寬度稍寬，但是其旁瓣衰減速度大于矩形窗的衰減速度，旁瓣電平低。而且，通過選取適當的τ1可以獲得無負旁瓣，可以抵制變換中的高頻干擾和泄漏，特別適合于有噪聲的場合。

表1 幾種窗函數的幅頻特性

2 離散頻譜梯形窗幅度比值校正法

下面來推導加梯形窗的離散頻譜校正公式。設單頻正弦信號x(t)的形式為

式中：A,α,φ分別為信號的頻率、幅度、初相位?，F在來考察這個信號在[0，T]上加梯形窗之后的頻譜

進一步整理可簡化為

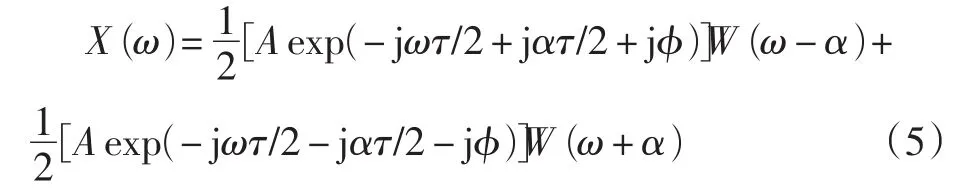
這里的W(ω)就是式（2）的梯形窗函數的窗譜。在這里忽略負頻率泄露的影響，只考慮ω＞0時的情況。這樣有

如果信號的真實頻率并不是正好落在離散頻譜的整數根上，如圖2所示。這時利用FFT變換所得到的頻率估計值就會有誤差，就需要進行頻譜校正。設真實頻率與FFT得到的最高幅值ab（譜線序號為k）之間的偏差為δ，幅值為X（k），次高譜線cd在k+1處，幅值為X（k+1），那么次高峰與真實頻率之間的偏差為1-δ。則

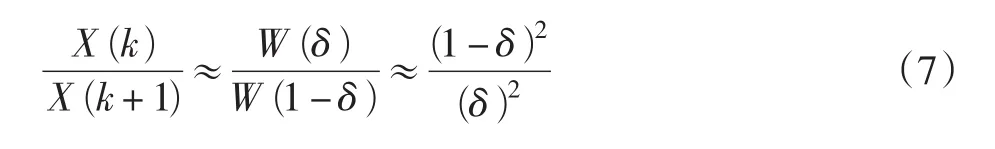
可以解出

式中：δ∈[-0.5,0.5]。

由式（8）可見，梯形窗的頻譜校正是利用了次高峰的峰值與最高峰的峰值之間的關系得到的。如果次高峰在最高峰的左邊，那么校正頻率為α?=(k-δ)Δf；如果次高峰在最高峰的右邊，那么校正頻率為α?=(k+δ)Δf。綜上所述，信號的實際頻率估計

式（9）就是離散頻譜梯形窗幅度比值法的校正公式。

通過上述分析，可以得到新算法的實現步驟如下：

1）令 X（m）=FFT（x（n），其中 x（n）是 x（t）的采樣序列。

2）查找abs（X（m））的最大值X（k），次大值X（k-1）或X（k+1）。

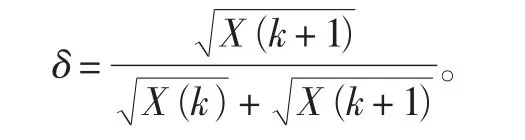
4）按照公式（9）估計信號的頻率。

3 仿真實驗

根據以上分析進行仿真實驗。設信號形式如式（3）所示。信號的幅值為A=1，φ=0，采樣點數N=512，采樣頻率fs=512 Hz。加矩形窗后的信號的頻率校正誤差和本文所提的梯形窗幅度比值法的頻率校正誤差的對比曲線如圖3所示?？梢钥闯觯瑹o噪聲時，矩形窗的校正精度要比梯形窗的校正精度高，但是當信號質量明顯下降時，即噪聲比較大時，對本文所提的離散頻譜梯形窗的校正精度影響較小，而對加矩形窗的校正精度影響較大。這說明梯形窗的抑制噪聲的能力較強。

圖4給出了兩種方法的頻率估計的均方根誤差RMSE與SNR的變化關系，此時，α=102.125 Hz。從實驗結果可見，無論是加矩形窗還是加梯形窗，這兩種算法的校正精度都會隨著信噪比的升高而逐漸趨近于真實頻率。這是因為這兩種算法都是從窗函數的數學定義出發來推導頻率的校正公式，因此校正頻率的精度較高。但同時也能看出，在信噪比較低時，梯形窗的校正效果要高于矩形窗；而信噪比高時，情況正好相反。這是因為梯形窗的旁瓣電平比較低，可以有效地抑制干擾，但主瓣寬度比矩形窗寬，因此在信噪比高時，其頻率分辨率不如加矩形窗時的頻率分辨率高。

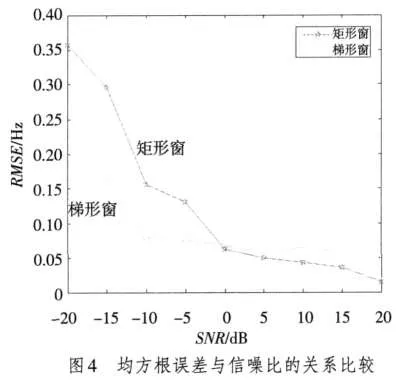
4 結論

筆者從梯形窗的數學定義出發，給出了一種加梯形窗的離散頻譜幅度比值校正法，利用最高譜線和次高譜線兩條譜線的幅度比值關系，推導了加梯形窗的離散頻譜校正公式，對加矩形窗和加梯形窗時的單頻正弦信號的頻率校正誤差進行了比較。仿真結果表明，該頻譜校正算法的校正精度在低信噪比時，明顯優于加矩形窗的校正精度，而且運算簡單，適合于低信噪比條件下的實時信號處理等場合。

[1]BURGESS T.On digital spectrum analysis of peri odic signals[J].J.A coust Soc.Am，1975，58（3）：556-567.

[2]GRANDKE T.Interpolation algorithms for discrete fourier transforms of weighted signals[J].IEEE Trans.Instrumentation and Measurement，1983，32（2）：350-355.

[3]黃柏圣，陳晨，許家棟.一種新的復正弦信號二維頻率估計算法[J].計算機仿真，2009，26（3）：198-201.

[4]張強，張頻，張明童.加三角窗的頻譜校正[J].振動與沖擊，2009，28（2）：96-98.

[5]齊國清，賈欣樂.插值FFT估計正弦信號的精度分析[J].電子學報，2004，32（4）：625-628.

[6]齊國清.幾種基于FFT的頻率估計方法精度分析[J].振動工程學報，2006，19（1）：86-91.

[7]謝明，丁康.頻譜分析的校正方法[J].振動工程學報，1994，7（2）：172-179.

[8]丁康，謝明.離散頻譜三點卷積幅值校正法的誤差分析[J].振動工程學報，1996，9（1）：92-98.

[9]齊國清，賈欣樂.基于DFT相位的正弦波頻率和初相的高精度估計方法[J].電子學報，2001，29（9）：1164-1167.

[10]黃云志，徐科軍.基于相位差法的頻譜校正方法的研究[J].振動與沖擊，2005，24（2）：77-79.

[11]丁康，江利旗.離散頻譜的能量重心校正法[J].振動工程學報，2001，14（3）：354-358.