基于非線性序轉(zhuǎn)換的層次分析模型

龐彥軍,劉立民,馬麗濤,劉開第

(河北工程大學(xué)理學(xué)院,河北邯鄲056038)

層次分析法(analytic hierarchy process,AHP)[1]是Saaty教授在二十世紀(jì)七十年代末提出的一種無結(jié)構(gòu)化決策方法,被廣泛應(yīng)用于涉及指標(biāo)重要性權(quán)重的眾多應(yīng)用領(lǐng)域[2-5]。AHP采用“兩兩比較”的方法,在準(zhǔn)則下對準(zhǔn)則支配的相鄰下層各項指標(biāo)通過構(gòu)造比例標(biāo)度判斷矩陣,并利用基于“一致性”檢驗的特征向量法(或冪法,或和法)對下層指標(biāo)排序,很好地解決了相鄰兩層指標(biāo)間的排序問題[6-7]。

然而對于三層及以上層次結(jié)構(gòu),需要在頂層目標(biāo)下對底層指標(biāo)按重要性大小排序,則必須解決以下兩個問題：一是在上層每一項指標(biāo)下對該指標(biāo)所支配的相鄰下層指標(biāo)排序;二是通過序關(guān)系轉(zhuǎn)換在頂層目標(biāo)下對底層指標(biāo)排序。AHP實現(xiàn)序轉(zhuǎn)換的方法為線性序轉(zhuǎn)換,這種方法僅適用于簡單遞階層次結(jié)構(gòu),當(dāng)遞階層次結(jié)構(gòu)為復(fù)雜結(jié)構(gòu)時,線性序轉(zhuǎn)換只能作為真實序轉(zhuǎn)換的一種近似。

本文分析遞階層次結(jié)構(gòu)的復(fù)雜性,將排序度量映射到高維狀態(tài)空間上,提出了復(fù)雜層次結(jié)構(gòu)序關(guān)系轉(zhuǎn)換的非線性方法,給出了遞階層次結(jié)構(gòu)指標(biāo)排序的一般方法。

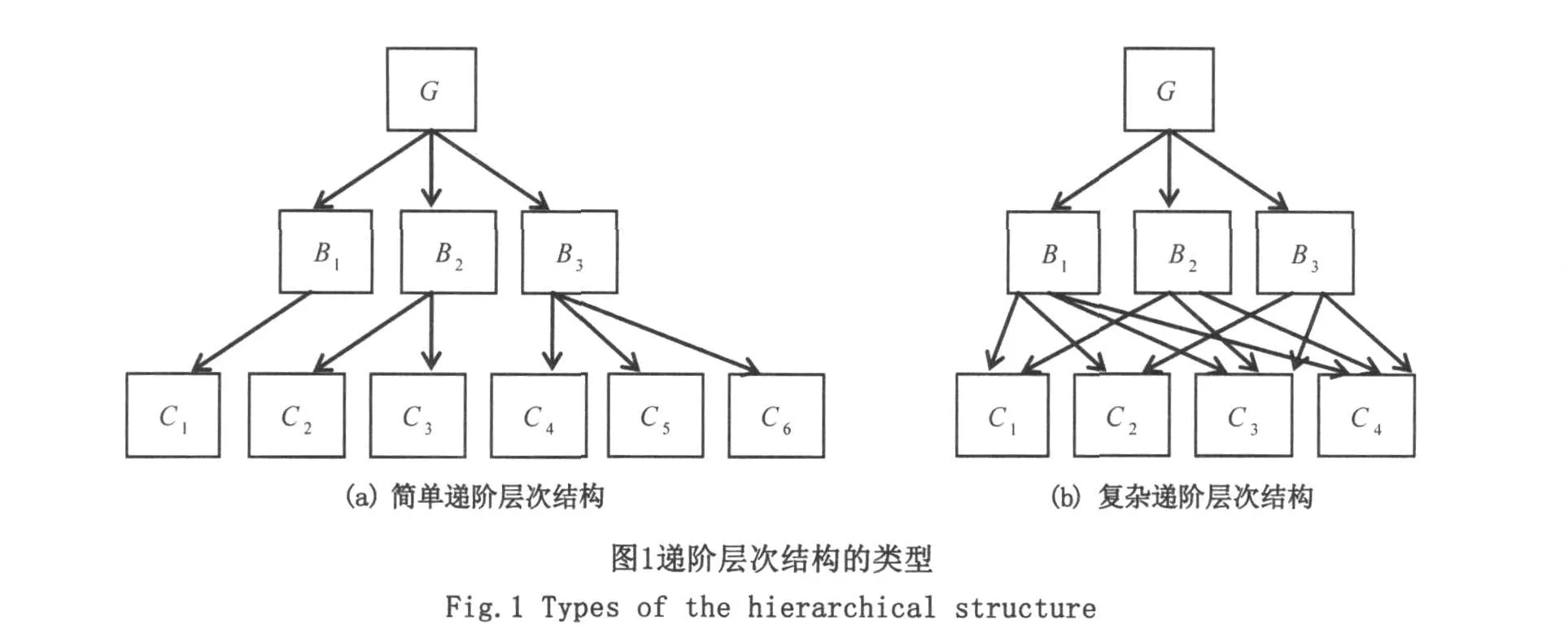
1 遞階層次結(jié)構(gòu)的類型

遞階層次結(jié)構(gòu)的復(fù)雜性由上、下層指標(biāo)間的不同聯(lián)接方式?jīng)Q定,分為簡單層次結(jié)構(gòu)及復(fù)雜層次結(jié)構(gòu)(圖1)。

簡單層次結(jié)構(gòu)的特點是,每一項底層指標(biāo)發(fā)生時,影響且只影響相鄰上層中一項指標(biāo)。只通過一項指標(biāo)傳遞到目標(biāo)G的序關(guān)系,是且只能是線性關(guān)系,對應(yīng)線性序轉(zhuǎn)換。

復(fù)雜層次結(jié)構(gòu)的特點是,當(dāng)一項底層指標(biāo)發(fā)生時,會同時影響相鄰上層至少兩項指標(biāo),此時,經(jīng)中間指標(biāo)B1,B2,B3,傳遞到G的序關(guān)系就不再是線性關(guān)系,而是非線性序關(guān)系,對應(yīng)序轉(zhuǎn)換是非線性轉(zhuǎn)換。

2 復(fù)雜層次結(jié)構(gòu)的非線性序轉(zhuǎn)換算法

以三層復(fù)雜結(jié)構(gòu)為例。

設(shè)由AHP法已求得底層n項指標(biāo)關(guān)于中間層指標(biāo)j(j=1-m)的排序向量

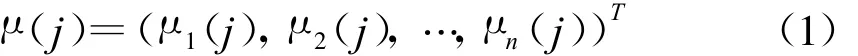
及m項中間層指標(biāo)關(guān)于頂層目標(biāo)G的排序向量

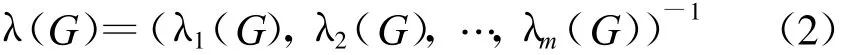
求在目標(biāo)G下對底層n項指標(biāo)排序。

2.1 難點分析

當(dāng)?shù)讓又笜?biāo)i發(fā)生時,目標(biāo)G同時接收到中間層m項指標(biāo)B1～Bm發(fā)送的關(guān)于指標(biāo)i的m種信息μi(j)(j=1～m),但是,無法得知每一個μi (j)究竟對目標(biāo)G提供了多少關(guān)于指標(biāo)i的“有效信息”,也無法得知這m種信息按著怎樣的“規(guī)律”融合。所以,通過某種線性運算得出指標(biāo)i關(guān)于目標(biāo)G的排序度量αi(G)僅是真實度量的一種近似。

本文通過把排序度量 μi(j)映射到能描述 μi(j)“重要性程度”的高維狀態(tài)空間上,分析 μi(j)在每個子空間上的映射值究竟對目標(biāo)G提供了多少關(guān)于指標(biāo)i的“有效信息”,并通過“信息融合”探索非線性序轉(zhuǎn)換的算法途徑。

2.2 排序度量到高維狀態(tài)空間的映射

步驟1：將指標(biāo)i對指標(biāo)j的影響程度μi(j)劃分為s=5個等級,設(shè){F1,F2,…,F5}是狀態(tài)空間F的一種劃分,滿足

Fi∩Fj=φ(i≠j)且∪5k=1Fk=F稱Fk(k=1～5)是第k種狀態(tài),也稱為第k類。

步驟2：令a=min{μi(j)},b=max{μi(j)},將區(qū)間[a,b]四等分,連同區(qū)間端點在內(nèi)的5個分點是a=a1＜a2＜a3＜a4＜a5=b在[a,b]上,以ak(k=1～5)作為F6-k類的標(biāo)桿值。構(gòu)造5個等級的標(biāo)準(zhǔn)隸屬函數(shù)α1(t)～α5(t),如圖2所示。

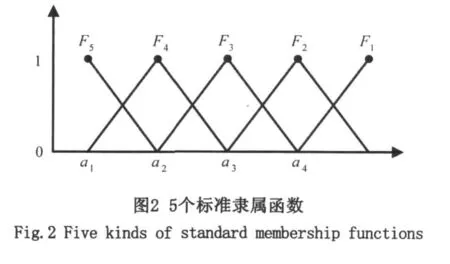
圖2中,F1類的隸屬函數(shù) α1(t)由折線a1a4F1表示;F2類的隸屬函數(shù) α2(t)由折線a1a3F2a5表示;F3類的隸屬函數(shù) α3(t)由折線a1a2a3F4a5表示;F4類的隸屬函數(shù)α4(t)由折線a1F4a3a5表示;F5類的的隸屬函數(shù) α5(t)由折線F2a2a5表示。

根據(jù)圖2的5個隸屬函數(shù),任一排序度量 μi(j)可表為一個5維向量：

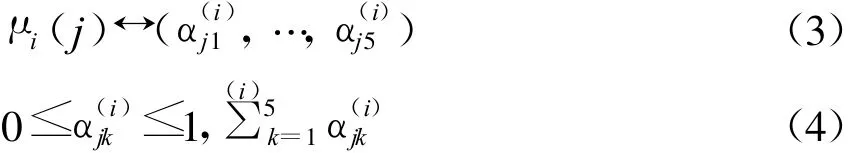
其中,α(i)jk—指標(biāo)j的k類隸屬度,表示指標(biāo)i發(fā)生時對指標(biāo)j的影響屬于Fk類的隸屬度。

2.3 隸屬度非線性轉(zhuǎn)換的算法步驟[8]

隸屬度的非線性轉(zhuǎn)換是在指標(biāo)隸屬度中包含著對目標(biāo)分類不起作用的冗余值,而清除冗余值的過程是非線性計算過程。

設(shè)指標(biāo)j關(guān)于目標(biāo)G的重要性權(quán)重為λj(G),目標(biāo)G的狀態(tài)轉(zhuǎn)移矩陣為U(i)(G)=()m×5。求指標(biāo)i發(fā)生時對目標(biāo)G的影響屬于Fk類的隸屬度(G)(k=1～5)。

令

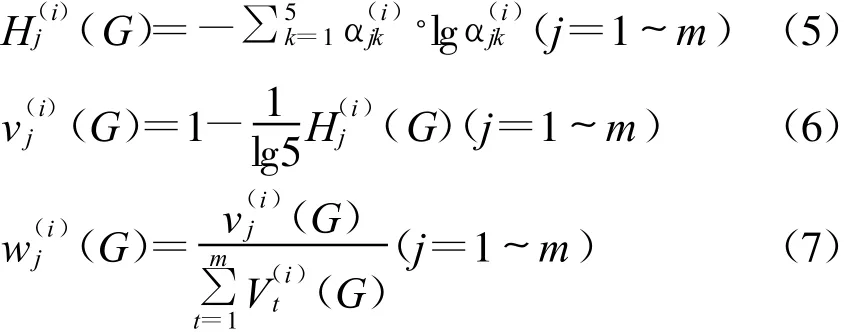
步驟1：計算指標(biāo)j的k類有效值

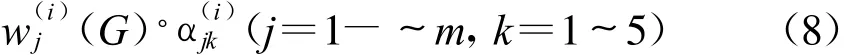
步驟2：計算指標(biāo)j的k類可比值

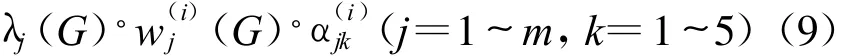
步驟3：計算目標(biāo)G的k類可比和

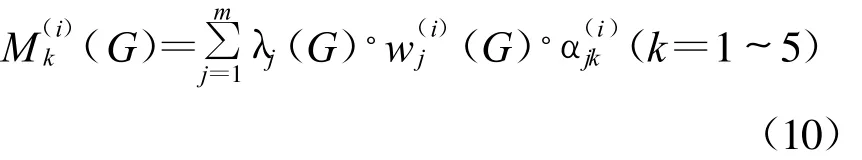
步驟4：計算目標(biāo)G屬于Fk類的隸屬度

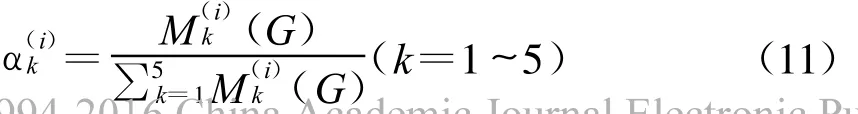
2.4 基于隸屬度的排序方法

令F1～F5的量化值依次為9,7,5,3,1,稱

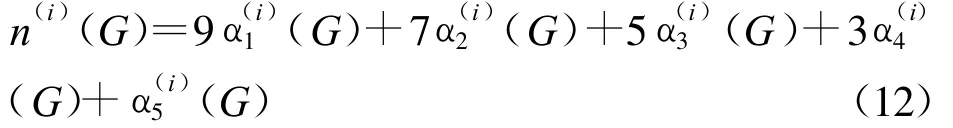
指標(biāo)i對目標(biāo)G的影響度。可按n(i)(G)的大小,在目標(biāo)G下對指標(biāo)i排序。

3 算例分析

某礦10號污水壩設(shè)計為一粘土斜墻防滲土石壩,建成蓄水后出現(xiàn)滲漏。根據(jù)場區(qū)工程地質(zhì)和水文地質(zhì)條件,擬采用4種防滲加固方案：P1是粘土鋪蓋+靜壓注漿;P2是深層攪拌樁;P3是高壓擺噴+靜壓注漿;P4是深孔注漿。

有6種衡量方案優(yōu)、劣的指標(biāo)：I1是治理可靠性,I2是安全性,I3是工程投資,I4是施工工期,I5是施工難易程度,I6是環(huán)境影響。這樣,方案排序構(gòu)成一個三層遞階層次結(jié)構(gòu)(圖3),G為總目標(biāo)。

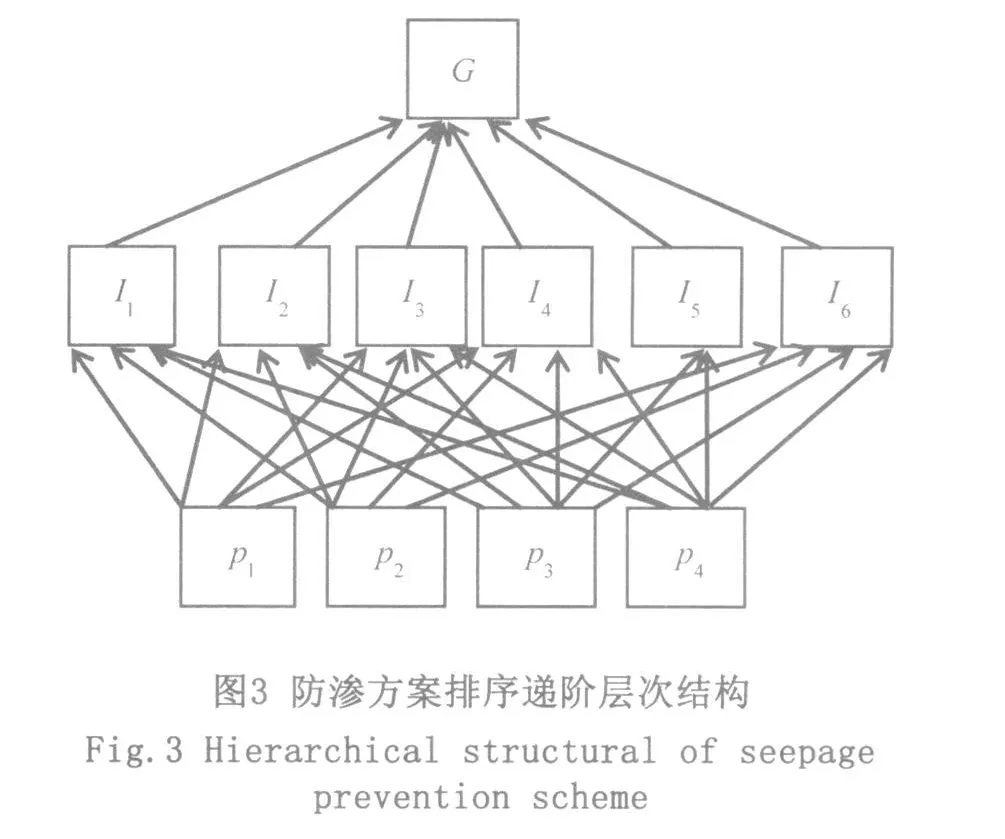
顯然圖3所示是一個復(fù)雜結(jié)構(gòu),對應(yīng)非線性序關(guān)系轉(zhuǎn)換。

在給定各方案關(guān)于6種指標(biāo)的邏輯評語集后,文獻[9]用層次分析法確定了中間層指標(biāo)I1～I6關(guān)于目標(biāo)目標(biāo)G的重要性權(quán)重向量

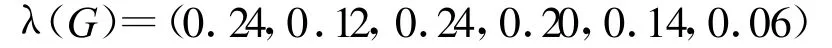
及4種方案關(guān)于6種指標(biāo)的排序度量矩陣：其中,U(G)4×6的第j列元素為各方案關(guān)于中間指標(biāo)Ij的排序度量。

方案排序步驟如下：

步驟1：構(gòu)造排序度量的隸屬函數(shù)

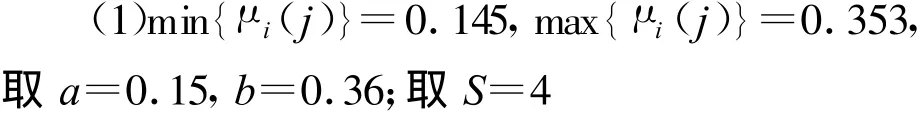
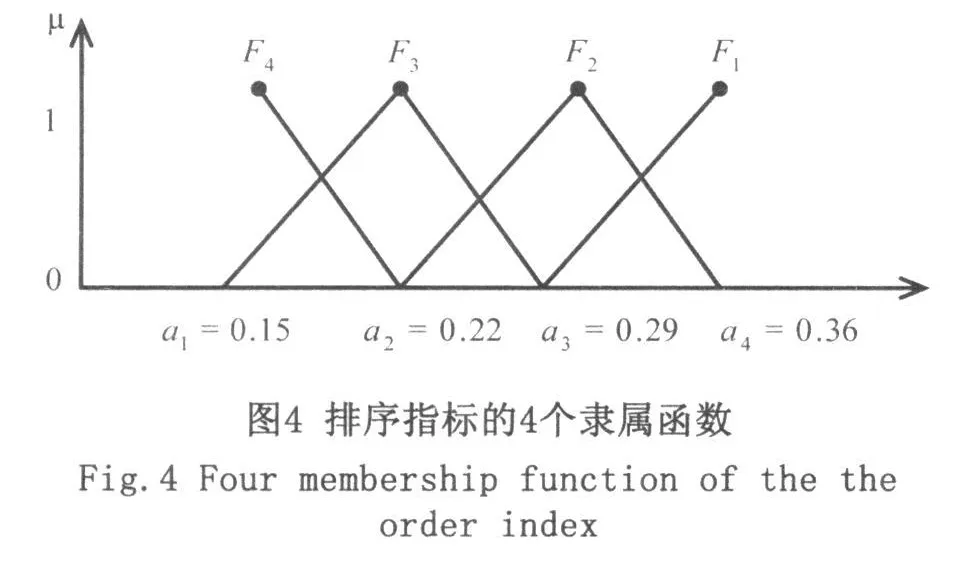
步驟2：構(gòu)建標(biāo)準(zhǔn)隸屬函數(shù)

以P1為例,P1關(guān)于6種指標(biāo)的排序度量,構(gòu)成目標(biāo)G關(guān)于P1的狀態(tài)轉(zhuǎn)移矩陣U(1)(G)：

步驟3：計算隸屬度向量

根據(jù)目標(biāo) G關(guān)于P1的狀態(tài)轉(zhuǎn)移矩陣 U(1)(G),得P1對G影響的隸屬度向量為：

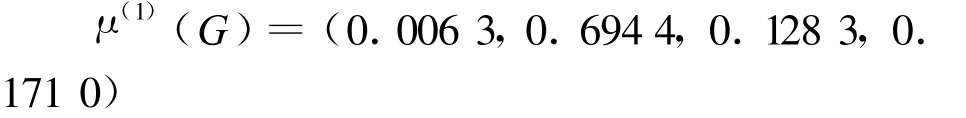
同理得方案P2,P3,P4對G影響的隸屬度向量為

步驟4：計算影響度

取F1～F4的量化值依次為4,3,2,1,各方案的影響度分別為

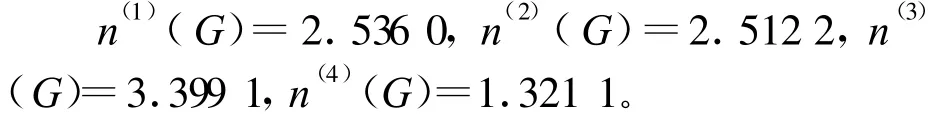
因為n(3)(G)＞n(1)(G)＞n(2)(G)＞n(4)(G),所以,方案P3最優(yōu),P1、P2次之,P4最差。

4 結(jié)語

遞階層次結(jié)構(gòu)中方案排序問題的本質(zhì)是實現(xiàn)非線性序轉(zhuǎn)換。通過把“排序度量”映射到高維狀態(tài)空間上,并利用區(qū)分權(quán)濾波算法實現(xiàn)了高維空間上隸屬度向量間的非線性轉(zhuǎn)換,可以作為解決復(fù)雜層次結(jié)構(gòu)中方案排序的一種實用方法。

[1]許樹柏.層次分析法原理[M].天津：天津大學(xué)出版社,1998.

[2]鄭賢斌,陳國明.基于FTA油氣長輸管道失效的模糊綜合評價方法研究[J].系統(tǒng)工程理論與實踐,2005, 25(2)：139-144.

[3]易俊,伍建林,史佩,等.二級模糊安全評估方法及其在油庫安全中的應(yīng)用[J].中國安全科學(xué)學(xué)報,2007, 17(6)：135-139.

[4]SAATTY T L.Decision making with the analytic hierarchy process[J].International Journal of Services Sciences, 2008,1(1)：83-98.

[5]戴佑斌,張尚根,周早生,等.模糊一致矩陣?yán)碚撛诘罔F深基坑支護方案優(yōu)選中的應(yīng)用[J].巖土工程學(xué)報,2005,27(10)：1162-1165

[6]周書敬,朱志,王飛.基于灰色層次分析的房地產(chǎn)投資決策[J].河北工程大學(xué)學(xué)報(自然科學(xué)版),2010, 27(2)：83-86.

[7]李樹文,李少雄,劉嘉瑋,等.水質(zhì)模糊綜合評價模型的改進[J].河北工程大學(xué)學(xué)報(自然科學(xué)版),2009, 26(3)：102-105.

[8]龐彥軍,周少玲,楊 珠,等.水質(zhì)模糊綜合評價模型的改進[J].河北工程大學(xué)學(xué)報(自然科學(xué)版),2007,24 (3)：89-93.

[9]陳永貴,鄒銀生,張可能.壩基防滲治理的多目標(biāo)模糊決策方法[J].湖南大學(xué)學(xué)報,2008,35(3)：15-18.