基于小波能量熵的水下目標磁場信號去噪

方 石 陳朝宏 殷正保

（1.海軍駐宜昌地區軍事代表室, 宜昌 443003； 2.中船重工集團第710研究所, 武漢 443003）

1 引言

小波變換理論為噪聲消除問題提供了一個新的思路。其主要思路是根據小波變換的線性，如果噪聲能量明顯小于信號能量，則與噪聲對應的小波系數也將明顯地小于與信號對應的小波系數；因此可通過將小于某一閾值的小波系數去除從而實現去噪。小波去噪中的關鍵問題是閾值的確定。目前主要有 MAD（Median absolute deviation）、MINIMAX（MINImaland MAXimal value）、SURE（Stein’s unbiased risk esti-mate[2]）和HYBRID（軟硬閾值混合） 等方法[3]用于確定閾值。但這些方法在確定閾值時都帶有一定的猜測性，因此去噪效果不穩定。

本文結合信息論中熵的理論，以及多尺度下小波熵的定義，在分析不同分解尺度上信號和噪聲不同的能量分布特性基礎上，通過對不同分解尺度上小波系數進行子帶分解，計算不同子帶分量的小波熵，利用最大小波熵自適應地選擇閾值，實現水下目標磁場信號的有效去噪。

2 小波變換及小波熵

設x（t）是平方可積函數，即x（t）∈L2（R），則x（t）的小波變換為：

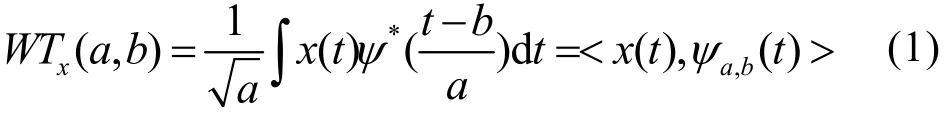
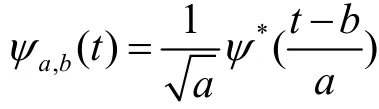
（1） 容許條件

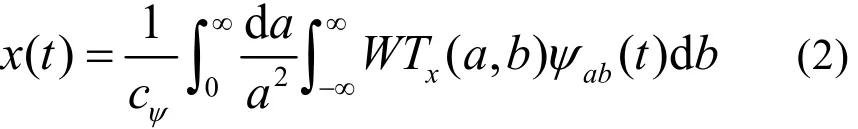
（2） 正規性條件

為使ψ（ω）在頻域上有較好的局域性能，要求|WTx（a,b）|隨a的減小而迅速減小，這就要求ψ（t）的前n階原點矩為0，且n值越高越好。即

P=1～n，且n值越大越好

對于（1）式，如果對尺度參數和位移參數按冪級數作離散化，即令a=a0j，b=ka0j則小波函數變為：

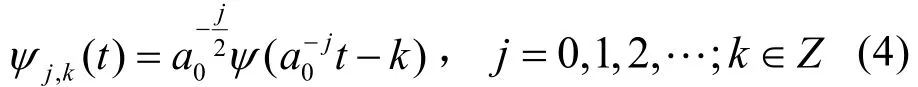
相應小波變換為

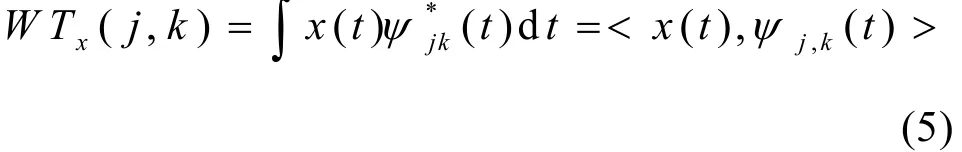
式（5）就是離散小波變換（DWT），其輸出結果便是小波序列的系數djk，信號x（t）可用小波基函數和小波系數表示為

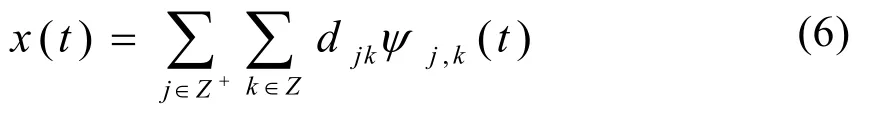
由小波標架理論可知，當小波基函數是一組正交基函數時，小波變換具有能量守恒性質，即

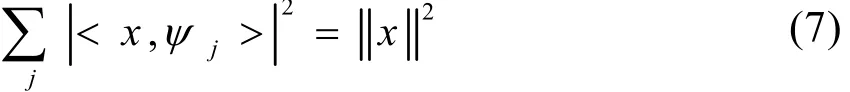
此時，單一尺度下小波系數的平方和就定義為該尺度下的小波能量[5]。

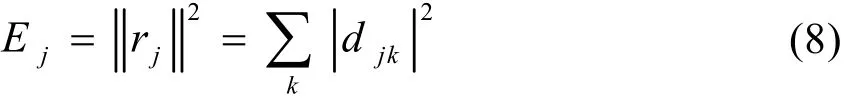
信號總能量就為各尺度下小波能量之和

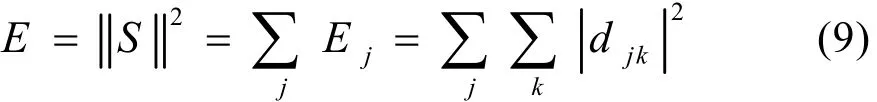
這樣，相對小波能量可定義為

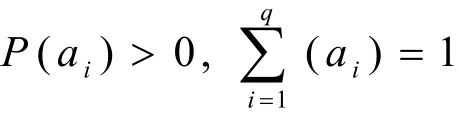
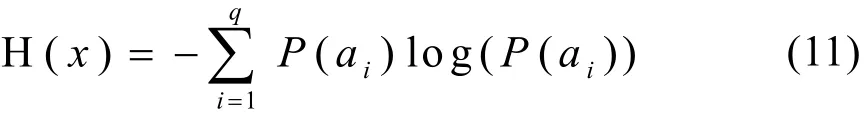
因此，信號熵值的大小實際上反映了其概率分布的均勻性，即信號的概率分布越接近無序的分布，其熵值也就越大；反之其熵值就越小。如果把小波變換的系數矩陣處理成一個概率分布序列，則由它計算得到的熵值就反映了這個系數矩陣的稀疏程度，也就是信號概率分布的有序程度，這種熵就稱作小波熵。如果將（11）式中的P（ai）換成（10）式中反映某一段信號能量強度比例的相對小波能量pj，則小波熵可定義為：

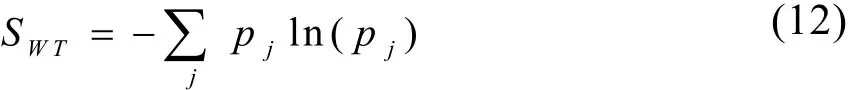
3 基于小波熵的閾值確定法

對于加性噪聲模型，經過正交小波變換后，能最大程度地去除有用信號的相關性，將能量集中在少數稀疏的、幅度相對較大的小波系數上。而噪聲對應的小波系數仍然互不相關，并將分布在各個尺度下的所有時間軸上，且幅度不是很大。如果在小波變換的各個尺度下保留那些集中了有用信號大部分能量的少數小波系數，而將其他點置零，或最大程度地減小，再利用處理后的小波系數做小波逆變換，就可實現對噪聲的抑制。因此，小波閾值在去噪過程中起到了決定性的作用，將直接影響到小波去噪的效果。

令觀察信號為

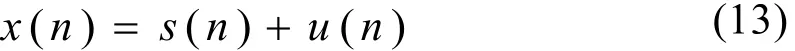
式中，s（n）為有用信號；u（n）是噪聲。記xλ是對小波系數施加閾值λ后重建的信號，uλ是xλ中殘留的噪聲，即uλ=xλ-s。由xλ近似s所產生的“風險函數”定義為

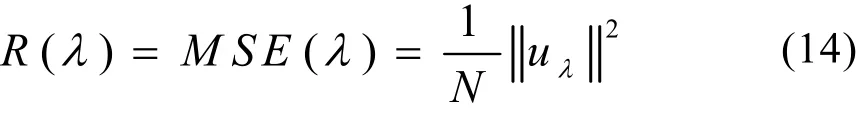
式中，MSE是均方誤差，N是數據長度。

文獻[6]和[7]證明了如果λMSE使E{R（λ）}為最小，則

式中，符號～表示漸進等效，λMSE稱為基于均方誤差的最小風險閾值。由于實際工作中最小均方誤差很難估計，因此，通常使用通用閾值

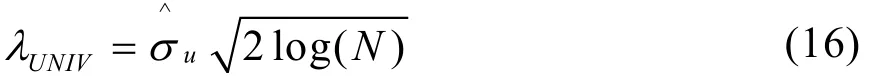
在閾值的確定過程中，將每一個分解尺度的高頻信息量都看成是一個單獨的信號源，將每一層高頻小波系數分成n個相等的小區間，計算各個小區間的小波熵，選取熵值最大的那個小區間的中值作為該尺度下噪聲的方差，再根據（16）式計算出各個尺度下的閾值，實現基于小波熵的閾值自適應選取。

3 基于小波熵的閾值確定法

采用艦船磁場仿真軟件生成一組探測距離413 m的航空磁性探潛試驗數據，如圖1所示，從圖中可以看出，目標信號完全被環境噪聲湮沒，無法進行分辨。基于Meyer小波基函數對一組信號進行5層的多尺度分析，得到的1～5層的細節信號，如圖2所示。從圖中可見，第1、2、3層細節信號的幅值較小，第4層細節信號的幅值有所增加，而第5層細節信號不但幅值增加，其包絡曲線構成的低頻成分和艦船磁場信號已非常相似。分別計算各層小波的功率譜，如圖3所示。其中，第4、5層分解信號的功率譜值較大，集中在0.04 Hz～0.2 Hz的頻帶，主要成分是背景極低頻磁干擾譜；第5層信號譜集中在0.03 Hz左右，目標信號包絡清晰可見。小波變換大大的提高了在0.5 Hz以下低頻段的頻率分辨率，且很好的將中心頻率各異的目標信號和背景信號分開來。但在0.05 Hz左右的位置信號疊加嚴重，必須選取合適的閾值進行濾波，才可以濾除幅值較大的背景噪聲，提取目標弱信號。圖4給出了基于不同閾值選取方法的小波去噪處理結果，其中（a）為采用固定軟閾值的小波去噪結果；（b）為采用SURE方法確定閾值的小波去噪結果；（c）為采用極大極小閾值的小波去噪結果；（d）為利用小波能量熵確定閾值方法的小波去噪結果。從圖中可以看出，基于小波能量熵的去噪結果明顯要由于其他三種方法。

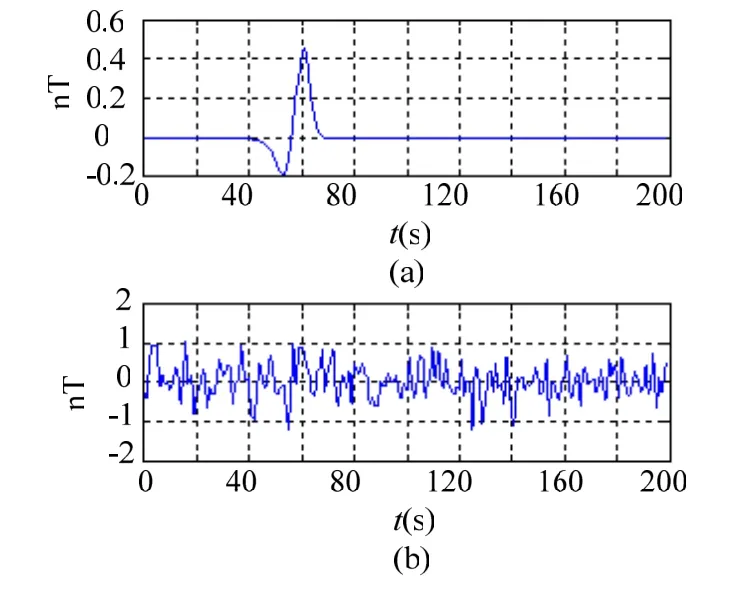
圖1 目標信號和觀測信號

圖2 目標磁場信號5層Meyer小波分析

圖3 各層小波的功率譜分析

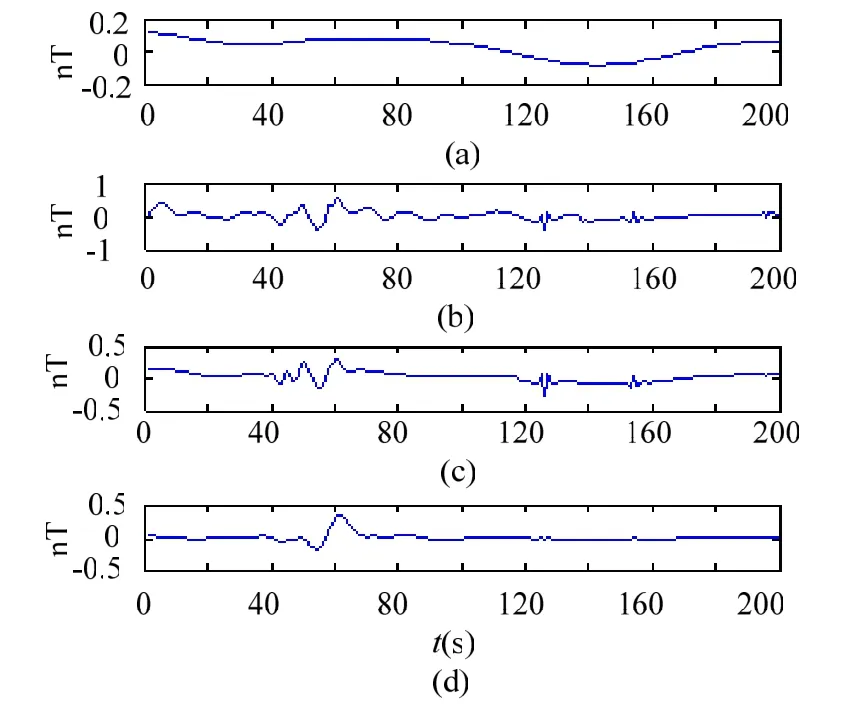
圖4 信號去噪結果

4 結束語

利用小波能量熵原理自適應地確定小波系數閾值的小波去噪方法，能夠在較強背景噪聲下實現對水下目標磁場信號的有效檢測，仿真結果表明，這種檢測方法能夠有效地提高信噪比，對水下目標磁場信號位置進行較為準確的定位，有效地提取有用信息。

[1] 葉平賢, 龔沈光. 艦船物理場[M]. 北京:兵器工業出版社, 1992.

[2] D L Donoho and I M Johnstone. Journal of the american statistical association,1995,90（432）:1200.

[3] B K Alsberg,A M Woodward,M K Winson,et al.Analyst,1997,122（7）:645.

[4] 傅祖蕓. 信息論——基礎理論與應用. 北京:電子工業出版社,2001;24-25.

[5] Svaldo A Rosso, Susana Blanco, et al. Wavelet entropy: a new tool for analysis of short duration brain electrical signals. Journal of Neuroscience Methods,2001;105:65—75.

[6] Donoho D L, Johnstone I M. Ideal de-noising in an orthogonal basis chosen from a library of bases. C R Acad Sci I-Math.1994,319:1317-1322.

[7] Jansen M. Noise reduction by wavelet three holding.New York: Springer-Verlag, 2001.

[8] 吳正國, 夏立, 尹為民. 現代信號處理技術[M]. 武漢:武漢大學出版社,2002.

[9] 印欣運, 何永勇. 小波熵及其在狀態趨勢分析中的應用[J]. 振動工程學報, 2004, 17（2）: 165-169.

[10] 張榮標, 胡海燕, 馮友兵. 基于小波熵的微弱信號檢測方法研究[J]. 儀器儀表學報, 2007, 28（11）:2078-2084.