基于水力旋流器三維數值模擬的結構參數研究
李 慧 張發廳
0 引言
水力旋流器是一種應用非常廣泛的液體非均相混合物的分離設備。自問世以來,有關其研究與應用方面的文獻已有很多,然而所涉及的大都是分級方面,應用于固—液分離方面的則比較少。由于其具有結構緊湊、成本低、處理量大、分離效率高并且可連續操作等優點,因而其在固—液分離領域的應用越來越受到關注。
單純通過實驗的方法[1,2]研究旋流器,周期長、成本較高且受到模型尺寸、人身安全和測量精度上的限制。因此,本文針對地下水除沙用的固—液分離水力旋流器,利用計算流體動力學(CFD)的FLUENT商業軟件包對其進行數值模擬。通過改變模型的結構參數,探討其對水力旋流器性能的影響,從而為水力旋流器優化結構參數,減少能耗提供一定的技術基礎和依據。
1 模型幾何結構尺寸
如圖1所示,柱體段長度h=300mm,插入深度S=100mm,旋流器錐角α=15°。
其余幾何參數如下:
a=40 mm;b=80 mm;De=85mm;D=250mm;B=60 mm; H=1 021mm。
為更符合實際工況,底流口延長一平行直管,長度為 50mm。

2 水力旋流器內流場的數值計算方法
2.1 湍流模型
目前可用于工程實際的模擬方法,仍是從Reynolds時均化方程出發的模擬方法,這就是常說的“湍流模型”[3],其基本出發點是利用某些假設,將Reynolds時均化方程中的高階湍流脈動關聯項用低階關聯項或時均量來表達,從而使Reynolds時均化方程組封閉可求解。
2.2 積分區域的離散化
在對指定的問題進行CFD計算之前,首先要將計算區域離散化,把它劃分成許多個子區域,并確定每個區域中的節點位置及該節點所代表的控制容積,從而生成網格。
2.3 求解方法的確定
將控制方程組離散變為代數方程后,接下來就是求解的問題了。水力旋流器內流場為時均定常、各向異性的強湍流旋流流動。針對水力旋流器的流場,一般采用SIMPLE,SIMPLER,SIMPLEC等系列壓力—速度修正算法求解。FLUENT軟件提供了SIMPLE,SIMPLEC和PISO三種處理壓力—速度耦合關系的算法。SIMPLEC是SIMPLE的改進算法,意為協調一致的SIMPLE算法,在該算法中可不再對壓力修正值進行欠松弛處理。PISO一般用于求解非穩態問題,而且對于動量方程與其他標量場強烈耦合的穩態問題,用PISO方法很不容易收斂。
因此,結合前人經驗,本文的研究采用穩態迭代法的 SIMPLEC算法。
3 結構參數對性能的影響
由模擬結果可分別得到各個結構參數對其性能的影響。
3.1 溢流管直徑對壓降的影響
溢流管直徑是一個很重要的結構參數,它一定程度上決定了內、外旋流的分界點位置,對壓降和分離效率的影響都較大。

表1 溢流管直徑—壓降關系表
本文在進口流量為 80 m3/h的情況下,即入口流速為6.94m/s時,對溢流口直徑分別為 70,85,95,100的旋流器進行了數值模擬,對比考察了溢流管直徑對壓降的影響。表 1列出了不同溢流管直徑下的模擬壓降值和經驗公式計算值。由數值預報的結果和經驗公式計算值可看出,隨著溢流管直徑的增大,靜壓降、動壓降絕對值、總壓降都隨之減小。作者認為,直徑較小的溢流管中流體的速度較大,即動能較大,因而靜壓能較低,靜壓降較大。同時,小直徑的溢流管的阻力損失相應也會增大,因此,總的壓降也較大。
3.2 溢流管直徑對分離效率的影響
表2列出了入口流速為 6.94m/s時,不同溢流管直徑下的模擬的分離效率和分級效率值。從表 2中可以看出,隨著溢流管直徑的增大,總的分離效率、分級效率均逐漸降低。粒徑為 3.95μm的顆粒的分離效率降低幅度較大,即所受溢流管直徑的影響較大,而粒徑為 27.2μm的顆粒分離效率幾乎不受溢流管直徑的影響。作者認為,當溢流管直徑增大時,內外旋流的分界點逐漸向筒壁外移,使得內旋流區域增大,外旋流區域減小,顆粒更容易卷入內旋流從溢流管逃逸而不能有效分離。同時,溢流管直徑的增大,使得短路流更容易發生,粒徑較小的顆粒很容易被短路流夾帶,因此對溢流管直徑變化較為敏感。盡管較小溢流管直徑分離效率較高,但是由前面的分析可知,較小的溢流管徑同時也會增大壓降,即增大能耗。因此,在實際工況中,應根據具體的生產要求,來確定所選擇的水力旋流器的溢流管直徑尺寸。
3.3 溢流管插入深度對分離效率的影響
一般情況下,固—液旋流器中的溢流管要向圓柱段內插入一定深度,來減少由于短路的作用而使進入旋流器頂部的分散相顆粒直接從溢流管排出從而降低分離效率。合理的溢流管插入深度有利于分離效率的提高。本文考察了一定進口流量的前提下,溢流管插入深度分別為80mm,100mm,105mm,125mm,150mm的情況下對分離效率的影響。表 3列出了不同插入深度下,分離效率和粒級效率的模擬計算值。
可以看出,隨著溢流管插入深度的增大,總的分級效率先增大,后又逐漸減小,其曲線出現了一個高效平緩區。該高效區大概區段在 100mm~125mm。各分級效率總體也呈現這樣一個趨勢,即效率先增大后減小,但是粒徑較大的顆粒的分離效率幾乎不受溢流管插入深度變化的影響。
因此,由數值模擬的結果可以看出,溢流管插入太淺,不利于短路流的抑制;但插入太深,會使中小顆粒不易分離,因而造成總的分離效率下降。
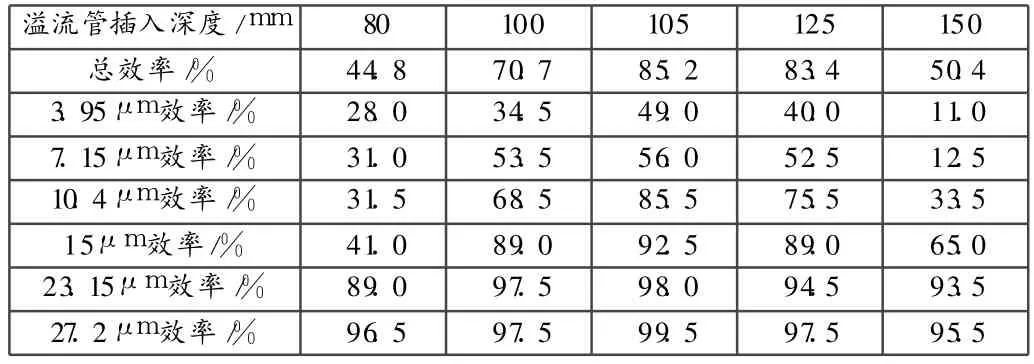
表3 溢流管插入深度—分離效率關系表
4 結語
本文使用FLUENT軟件,采用貼體坐標法的網格劃分,通過對固—液分離用水力旋流器的數值模擬,深入研究了結構參數對旋流器性能的影響。在入口流量一定的情況下,隨著溢流管直徑的增大,靜壓降、動壓降絕對值、總壓降都隨之減小,然而其分離效率也隨之減小,所以應兼顧考慮能耗與壓降這二者的關系。隨著溢流管插入深度的增大,總的分級效率先增大,后又逐漸減小。溢流管插入太淺,不利于短路流的抑制;但插入太深,會使中小顆粒不易分離,因而造成總的分離效率的下降,其插入深度存在一個高效取值區。
[1] Kelsall D.F..A Study of the Motion of Solid Particle in a Hydraulic Cyclone[J].Trans.Instn Chem.Eng.,1952,30(1):87-108.
[2] Brad ley D.,Pulling D.J..Flow Patterns in the Hydraulic Cyclone and Their Interpretation in Terms of Performance[J]. Trans.Instn.Chem.Eng.,1959,37(2):34-35.
[3] 賀友多.傳輸過程的數值方法[M].北京:冶金工業出版社, 1991:111-115.
[4] Dai.G.Q.,L.J.M.,Chen.W.M..Numerical Prediction of the Liquid Flow within a Hydrocyclone[J].Chemical Engineering Journal,1994,7(4):217-223.
[5] He.P.,Salcudean.M..A Numeirical Simulation of Hydrocyclones[J].Trans.Instn.Chem.Eng.,1999,77(Part A):429-439.
[6] 鄒 寬,楊 茱,曹 瑋,等.水力旋流器湍流流動的數值模擬[J].工程熱物理學報,2004,25(1):127-129.

