淺議自由網平差與程序設計

王娟，王東

(南通市現代測繪工程院，江蘇南通 226008)

淺議自由網平差與程序設計

王娟?，王東

(南通市現代測繪工程院，江蘇南通 226008)

簡單討論自由網平差中的秩虧自由網平差和自由網擬穩平差的原理，分析公式，結合VB語言編程，簡化自由網平差計算過程，并用實例進行水準測量數據平差處理。

自由網平差；秩虧自由網平差；擬穩平差；VB

1 秩虧自由網平差，擬穩平差以及假設檢驗的原理與公式

1.1 秩虧自由網平差原理與公式

變形觀測中，水準監測網一般可歸納為兩種類型:一是所布網中部分點是不動點或相對不動點構成基準，對網中其他點進行監測；二是網中全部點是否移動要通過觀測數據分析才能判定。對于前一類型監測網，各期都進行固定基準或擬穩基準的經典平差，但要對基準的穩定性進行假設檢驗。對于后一類型的監測網，一般先按重心基準進行秩虧自由網平差，通過觀測數據統計檢驗分析，找出網中相對穩定點，用擬穩平差對監測點的位移進行分析。

設某水準觀測數為n，必要觀測數為t，控制網中全部點數為u，秩虧自由平差的誤差方程型為:

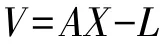
按最小二乘法原理:

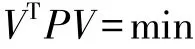
法方程為:

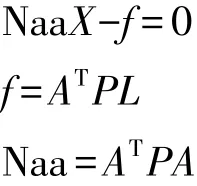
式中R(Naa)＝R(A)＝t＜u，Naa為奇異陣，其凱利逆不存在，得不到唯一解。秩虧數d＝u－t等于控制網的必要起算個數，對于水準網，必要一個點的起算高程，所以d＝1。本例采用Mittermayer1972年發表的附加條件法，運用數學工具使法方程系數陣零特征值對應的特征向量構成矩陣S。附加條件:

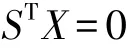
按照最小二乘原則，作函數:

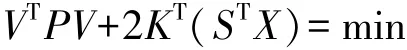
得到法方程:

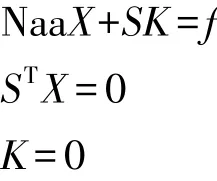
得到解為:

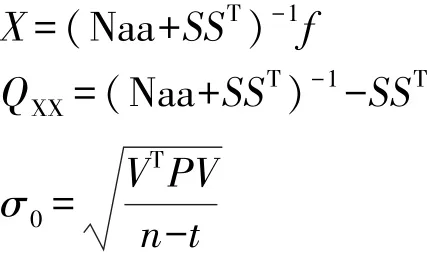
1.2 假設檢驗的原理與公式

兩期變形點坐標值之差異，并不一定反映點位的變動，它也可能是測量誤差引起的。為了探明這些差異主要是誤差干擾還是變形造成的位移，需要進行位移量顯著性檢驗，本文采用t檢驗法，步驟如下:

(1)檢驗的原假設H0是ξⅡ＝ξⅠ，即該點坐標理論值兩期相同，自然無位移存在；如果拒絕原假設H0，則接受備假設H1，認為位移存在。

(2)做統計量t，當原假設H0成立，則:

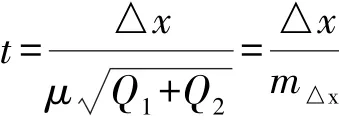
(3)選定顯著水平α，查t分布表得tα/2，如果｜t｜＞tα/2，則拒絕H0，位移顯著可信，否則，認為變形不可信。

1.3 擬穩平差的原理與公式

如果檢測網中的確有一部分點相對于另一部分點是相對穩定的，則以網中點的高程或坐標作為未知數，就有穩定未知點和不穩定知點兩類。設不穩定未知數的改正值為X1，穩定未知數的改正值為X2，設有t1個穩定點，進行擬穩平差。誤差方程為:

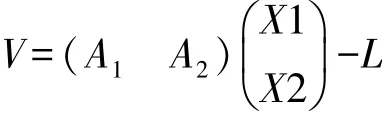
按最小二乘法原理:

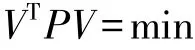
法方程為:

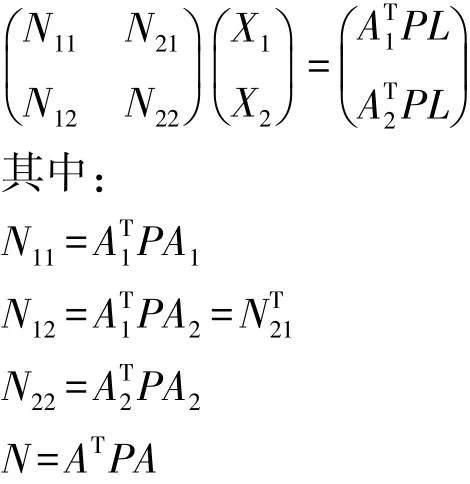
R(N11)＝t1，N11滿秩，R(N)＝r，N奇異，上式不能得到唯一解。本文中的擬穩平差解算方法采用我國周江文研究員針對變形監測網提出的廣義逆的方法。

附加X2的最小范數條件:

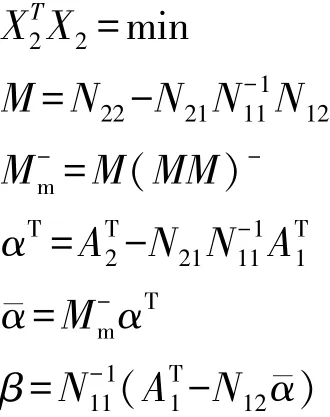
其中(MM)－為MM的廣義逆矩陣，得到方程解如下:

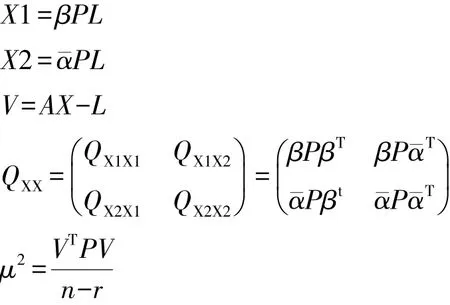
2 實例計算

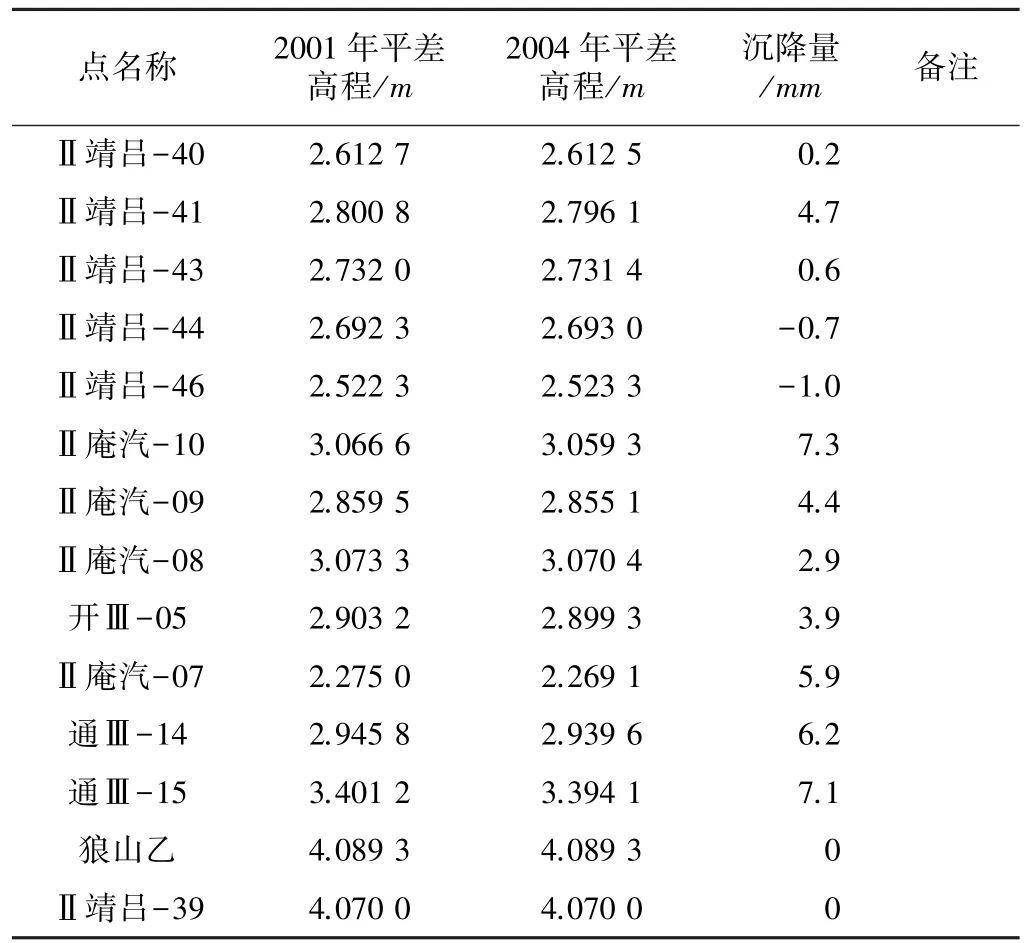
本文以江蘇南通蘇通大橋北接線區2001年和2004年兩期的地面沉降二等水準觀測數據作比較，先根據經典自由網平差結果統計點位沉降量，再用自編的秩虧和擬穩平差計算程序處理兩期觀測數據，對統計結果加以驗證，說明程序的可行性與實用性。經典自由網平差采用“Ⅱ靖呂－39”為唯一起算點、擬穩網平差選取“Ⅱ靖呂－39”和“狼山乙”兩個基巖點作為起算點，主要基于以下原因:上述兩點為南通市狼山風景區內兩個淺層基巖點，上世紀八十年代初由江蘇省測繪局選埋，自建成以來，江蘇省南通地震臺在該地區進行的斷層定點形變測量每隔一個月均聯測一次，近三十年的觀測結果顯示，點位穩定，與周圍其他基巖點的高差年變化量在1 mm以內，因此可以作為變形監測網內的所謂不動點。水準路線圖如圖1所示，兩期的野外觀測數據如表1所示。

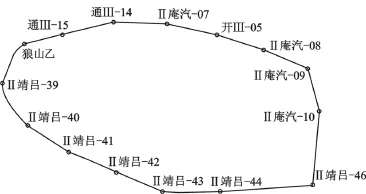
圖1 水準路線圖

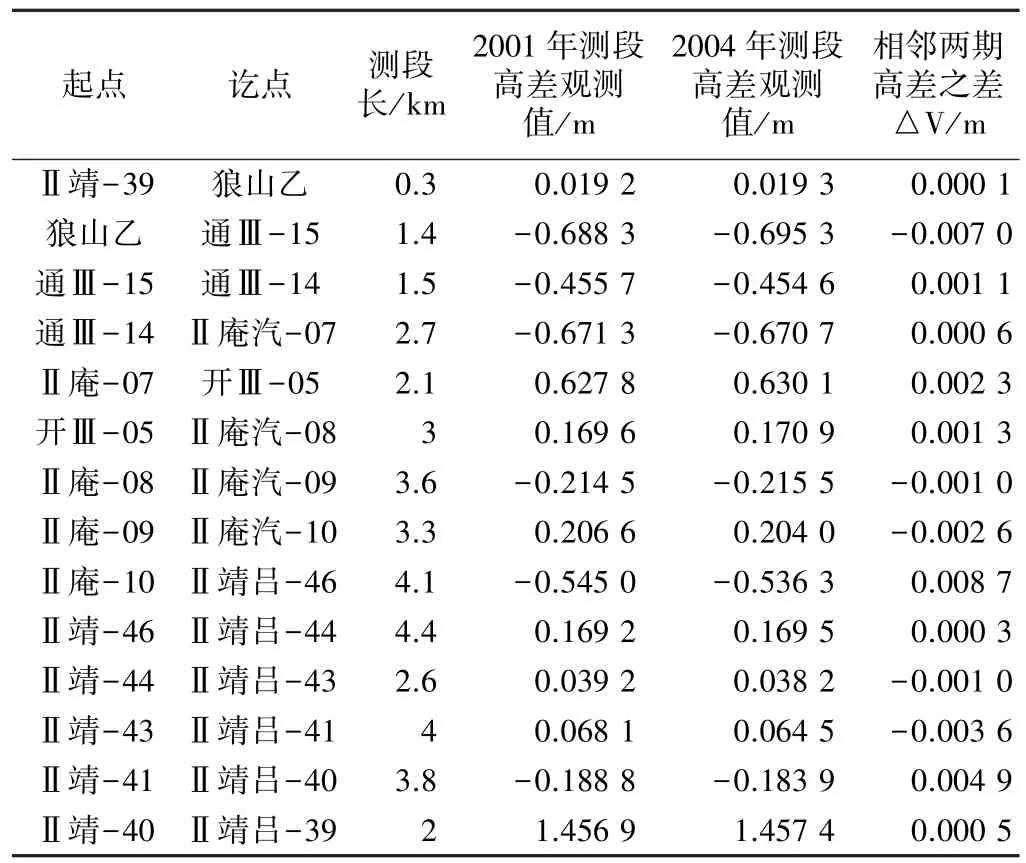
兩期觀測數據結果 表1

兩類平差的計算公式和步驟如下:

秩虧網平差，誤差方程V＝AX－L為:

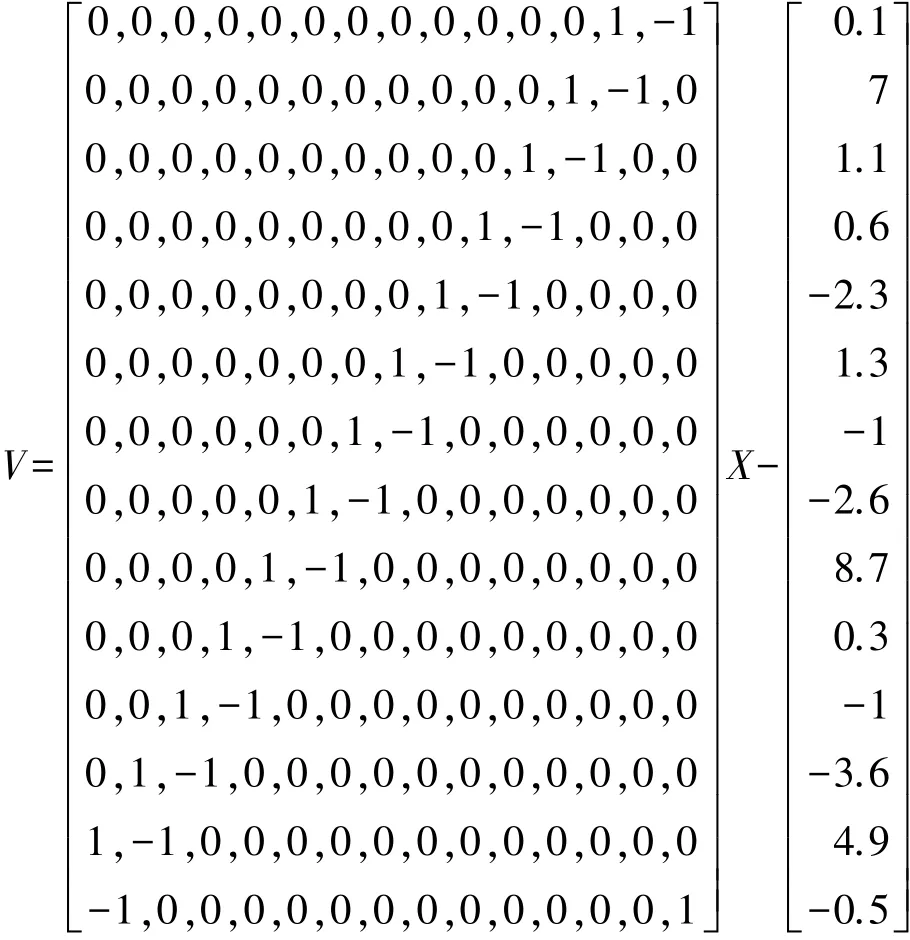
附加條件:

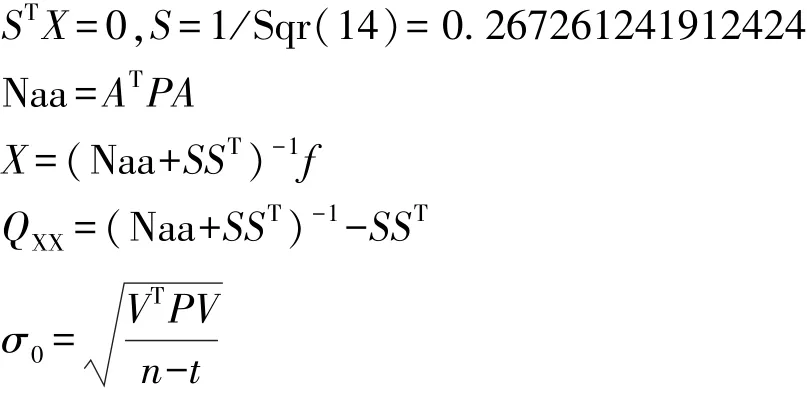
擬穩網平差，狼山乙，靖呂39為兩個已知穩定點，誤差方程為:

經典自由網平差統計結果 表2

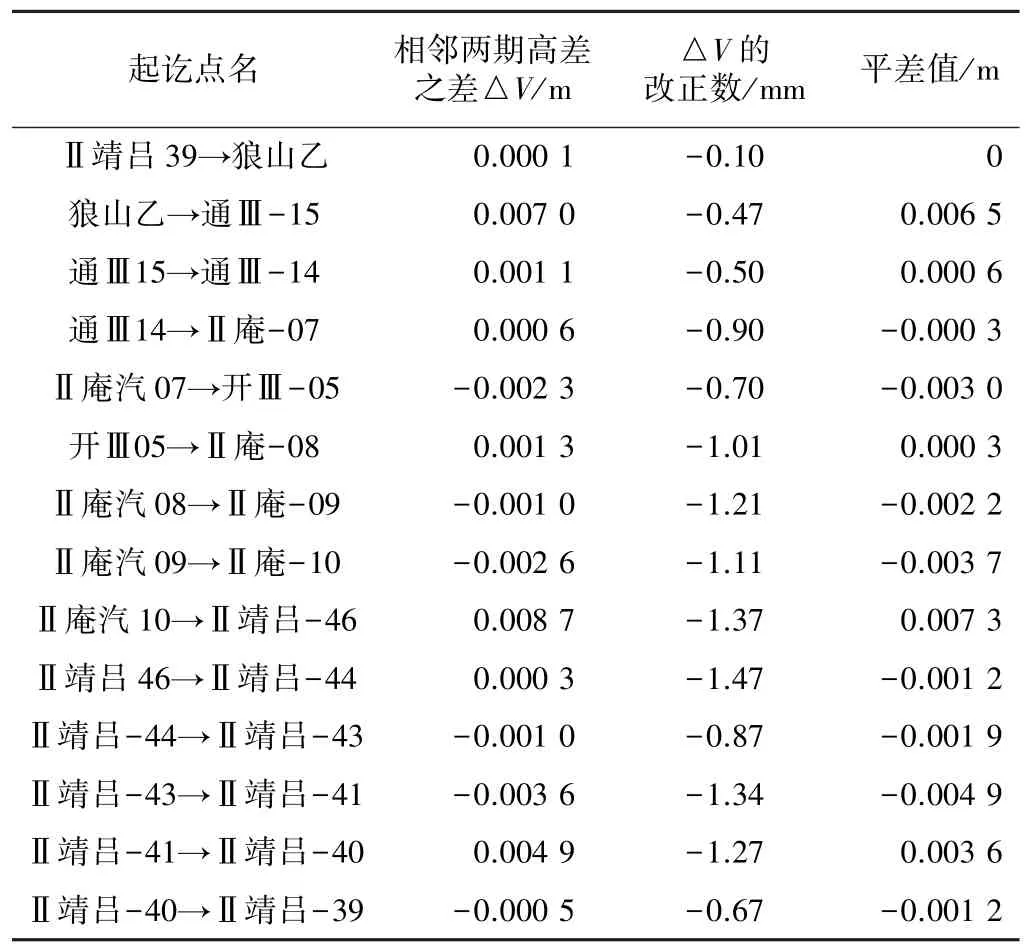
相鄰兩期測段高差變化平差結果 表3

運用上面的已知數和計算方程式，計算出△X和△V改正數如表3、表4所示，具體解算過程全部由軟件實現。數據處理時由于采用各點的近似高程值，因此可設相鄰兩期各點高程變化之差全部為零。從表3中可以看出，用以討論的擬穩與秩虧平差計算，所求得的△V的改正數相同，這是因為這兩種平差的高差之差改正數都是由公式VTPV＝min決定的。從表4中可以看出，兩類平差文件中的各點高程變化之差改正數△X的差值相同，其絕對值均為2.829 3 mm，這是兩者(一維)的基準差。而擬穩平差中的擬穩點“Ⅱ靖呂39”和“狼山乙”的△X的和為0，這是由X2的最小范數XT2X2＝min決定的。

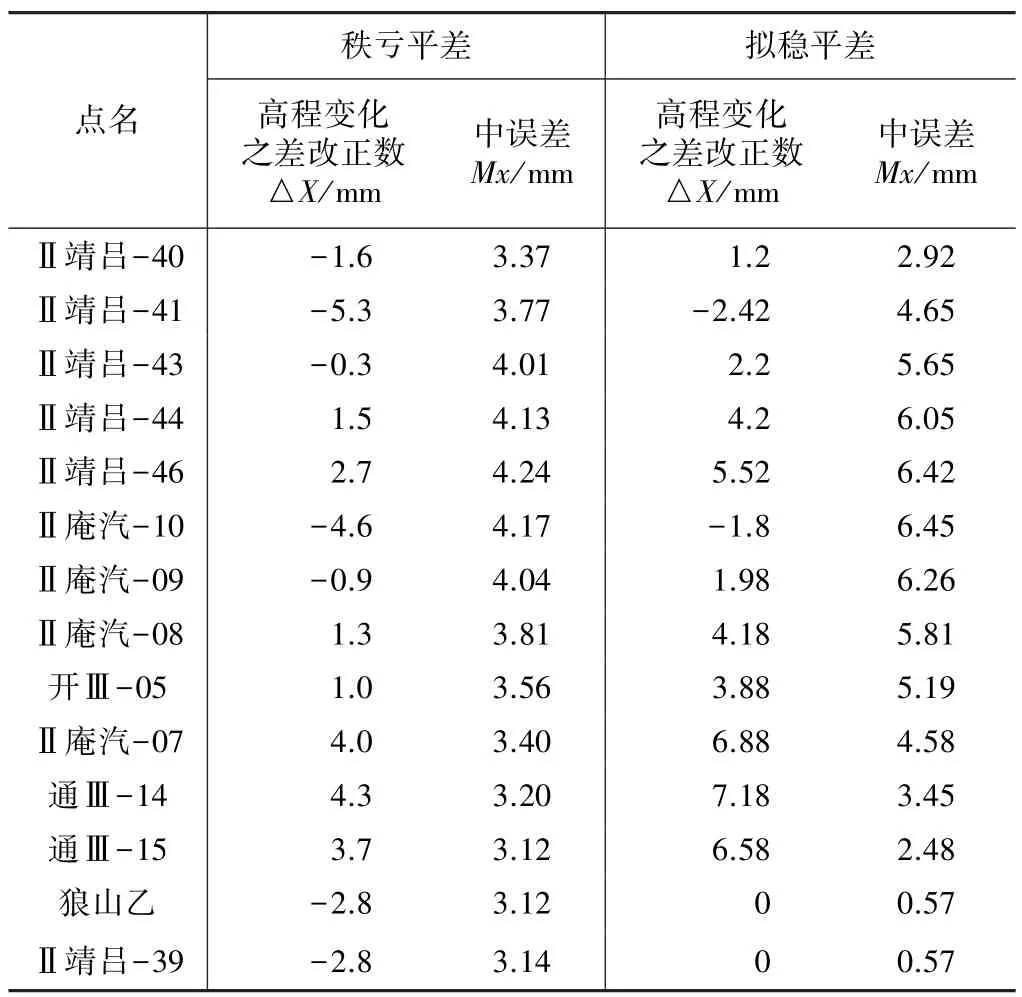
點位高程變化平差結果 表4

3 程序的實現

本文采用本人較為熟悉的VB語言編程實現秩虧和擬穩自由網平差計算，在一個程序中同時設置秩虧和擬穩平差計算，如果沒有穩定基準時先做秩虧自由網平差，通過觀測數據統計檢驗分析，找出網中相對穩定點，再用擬穩平差對監測點的位移進行分析。

4 結 語

秩虧自由網平差方程變化量相對擬穩平差要均勻。擬穩平差中擬穩點高程變化量減小，突出變形點。這一結果說明，如果在測區中的變形量變化較均勻，就應采用重心基準用秩虧自由網平差。如果擬穩點確實存在，采用重心基準將導致變形量的均勻分配而失真，采用擬穩基準就能相對正確判斷各點的變形量。本例中，在秩虧網解算中，兩個穩定的基巖標，實際上最為穩定，但是秩虧網平差中，這兩點的△X改正數并不是最小，并沒有真實反映其變形量，而采用擬穩平差計算時，兩點的變形量△X改正數為0，比較符合真實情況，這一結論在比較各點的沉降量大小(表2)與高程變化之差改正數△X的大小(表4)后得以驗證，兩者大小的絕對值基本是呈大小一致對應關系，說明程序設計運算結果是可靠的。

[1] 陳華生，牛又奇，孫建國.Visual Basic程序設計教程[M].蘇州:蘇州大學出版社，2000

[2] 計算機職業技術聯盟.Visual Basic程序設計基礎教程與上機指導[M].北京:清華大學出版社，2003

[3] 陶本藻.自由網平差與變形分析[M].北京:測繪出版社，1982

[4] 岳建平，田林亞.變形監測技術與應用[M].北京:國防工業出版社，2007

The Brief Discussion of Free net Adjustment and Program Design

Wang Juan，Wang Dong
(Nantong Modern Surveying and Mapping Engineering Institute，Nangtong 226008，China)

This paper briefly introduces the Principle of free net adjustment，including quasi－stable adjustment of rankdeficiency network and adjustment of rank deficiency free network，using the art of vb programing to solve Leveling Data adjustment.

free net adjustment；quasi－stable adjustment of rankdeficiency network；adjustment of rank deficiency free network；visual basic

1672－8262(2010)03－122－04

P207

B

2010—09—02

王娟(1982—)，女，助理工程師，主要從事軟件開發。