利用圖形分析法計算固體物質的溶解度

嚴西平 薛 磊

（江蘇省蘇州市立達中學江蘇蘇州215003）

利用圖形分析法計算固體物質的溶解度

嚴西平 薛 磊

（江蘇省蘇州市立達中學江蘇蘇州215003）

有關固體物質溶解度的計算,是初中化學中溶液知識部分的重要內容之一,也是教學難點之一,教學效果一直不是十分理想。其主要原因在于,一方面,在現用的教材中關于溶解度的計算問題只字未提,更別說解答的思路和格式的示范；另一方面,對于溶解度的概念及計算相對于溶液的溶質質量分數計算來講,較為抽象,不太容易理解與掌握。特別是遇到一些數據或過程不太直觀的計算題,很多學生都出現了捉襟見肘的尷尬情形。為此我們在教學中嘗試了“建?！薄磮D形分析法,具體如下。

一、圖形分析法的理論依據與思考過程

1.理論依據

溶液的特點就是均一性和穩定性。因此,在某一溶液中,任意一部分的溶液的組成及溶質的質量分數都是相同的。對于一定溫度下的某飽和溶液中,溶質的質量、溶劑的質量及溶液的質量之比是固定的,存在一定的比例關系。

2.思考過程

圖形分析法的思考過程,實際上就是利用數學建模的思想。利用數學的思維方式,將化學的計算題中比較抽象的情景建構成比較形象的數學圖像模型,借助于數學的思考與解題方法來處理化學的計算問題。

3.圖示思考與分析過程

如果圖1表示某溫度下的KNO3的飽和溶液,我們可以假設溶液存在一個假想的“膜”,將飽和溶液強行分割為“互不混合”的KNO3和水這兩個獨立部分,如圖2：

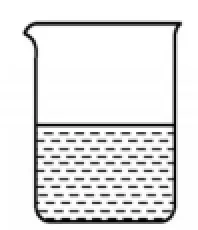
圖1

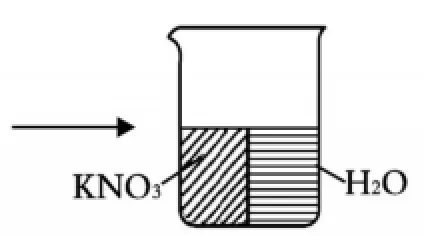
圖2

如果圖1表示某溫度下的KNO3的不飽和溶液,我們則可以將其假設分為三部分,即①KNO3固體、②能與固體恰好形成飽和溶液的水、③多余的純凈水,如圖3：

在不改變溫度的條件下,將KNO3不飽和溶液轉化為飽和溶液,可以通過蒸發溶劑或增加KNO3這兩種途徑。從圖形角度考慮,通過移去③,就變成了圖4所示的“飽和形狀”,或通過添加④填補“空缺”,也能形成如圖5所示的“飽和形狀”。

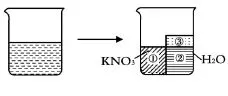
圖3

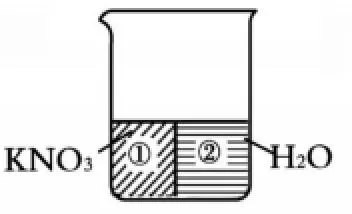
圖4

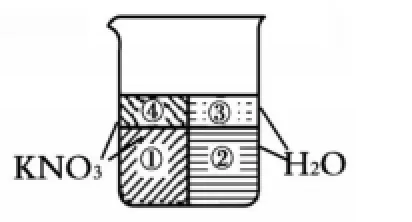
圖5

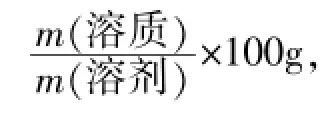
二、例題分析與解答

例1.60℃時,將90gKNO3加入75g水后充分振蕩后,仍有7.5g沒有溶解,求60℃時KNO3的溶解度。

分析與解答：根據題意,（90g-7.5g)KNO3與75g水混合,恰好能夠達到飽和,可畫出如圖6。根據固體溶解度的定義,只需將圖中水的質量“補”為100g,它所對應的KNO3質量便為該溫度下KNO3的溶解度,見圖7[其中的m4即未溶解的7.5gKNO3,m2+m3=100g,m1+m4=S（KNO3)]。

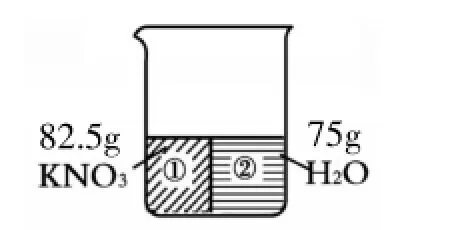
圖6

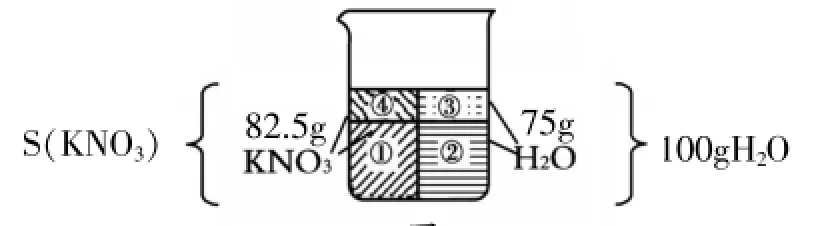
圖7

根據如圖5的討論,可得到比例式：

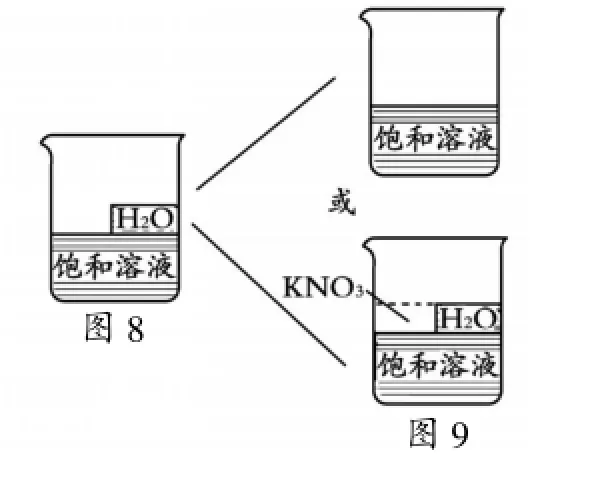
例233℃時,有250g硝酸鉀溶液,若向該溶液中加入30g硝酸鉀,則恰好達到飽和；若原溶液恒溫蒸發掉60g水,也恰好成為飽和溶液。求33℃時硝酸鉀的溶解度。

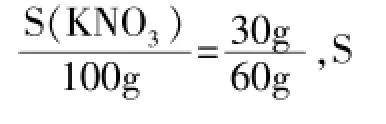
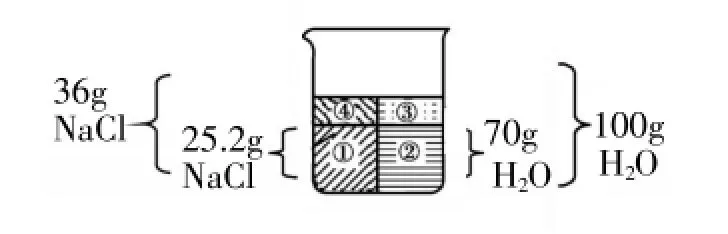
例3NaCl在20℃時的溶解度是36g。在20℃時,將30gNaCl加入到70g水中,充分溶解,所得NaCl溶液中NaCl的質量分數為（)

A.26.5%B.30%C.36%D.43%

分析與解答：利用圖形分析法,我們可以看出,m1顯然小于36g。根據比例,m1/70g=36g/100g,m1=25.2g。故可以用下式直接計算NaCl的質量分數：（當然也可以用25.2g/25.2g+70g計算,結果相同。)

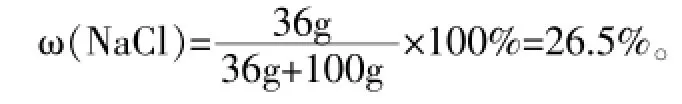
三、結論

通過構建有意義的具象,彌補了初中生抽象思維比較薄弱的不足,對于理解溶液的組成、掌握溶解度的概念和相關計算有積極的促進作用。教學效果較之傳統的“公式法”或“列表分析法”有明顯的改善,特別是學生容易掌握并能在解題中主動運用圖形分析法建構解題思路。當然該方法在用于改變溫度的情況下分析溶液的組成或計算溶解度方面還存在一定的局限,有待進一步完善。

1008-0546（2011）10-0091-02

G633.8

B

10.3969/j.issn.1008-0546.2011.10.046