鐵路鋼筋混凝土連續梁橋靜力彈塑性抗震分析

楊智玲

(沈陽鐵道勘察設計院有限公司，沈陽 110013)

我國是一個多地震的國家，鐵路橋梁作為生命線工程重要組成部分，其抗震性能好壞對于震后救援工作具有非常重要的意義。大地震發生時，結構不可避免地進入彈塑性工作階段，彈性反應譜分析無法直接反映結構的一些非線性特性。近些年來，靜力彈塑性分析作為一種簡單而有效的抗震評估方法，在建筑結構抗震設計評估中得到了廣泛應用，但在我國尚未應用于橋梁結構設計分析。本文以某鐵路鋼筋混凝土連續梁橋為例，對該橋進行靜力彈塑性抗震計算，并與彈性反應譜分析結果對比，對相關問題加以探討。

1 計算模型的建立

1.1 橋梁概況

該橋全聯長176 m，跨徑布置為(48+80+48)m預應力混凝土連續箱梁。上部結構為單箱單室單線箱梁，混凝土采用 C50。主梁頂板寬 7.2 m，底板寬4.2 m，墩頂部位梁高5.8 m，跨中部位梁高3.0 m，箱梁梁底采用1.6次曲線變化。橋墩高16 m，采用矩形實體橋墩，界面尺寸為4 m×6 m。橋墩混凝土采用C30，配筋主筋采用HRB400，直徑32 mm雙層布筋，箍筋采用HRB335，直徑16 mm，間距0.1 m。墩底采用12根直徑3 m的挖孔灌注樁基礎。

1.2 有限元模型

通過有限元方法對橋梁結構進行動力分析，首先需要建立合理的計算模型。包括上部結構和下部結構單元的選取和離散劃分、支承部位的模擬、墩臺邊界的處理以及荷載的確定。本文基于大型有限元軟件MIDAS Civil 2010，建立全橋模型。其中主梁和橋墩采用空間梁單元模擬，支座采用線性彈簧單元模擬。考慮了樁土的相互作用，采用6根彈簧表示墩底的約束條件。全橋有限元模型如圖1所示。

圖1 有限元計算模型

2 模態與反應譜分析

2.1 模態分析

結構自振特性決定結構的動力響應，同時也是反應譜計算的基礎。常規模態分析為線性的，結構自振特性主要與結構剛度與質量的分布有關。基于前述模型，綜合考慮該橋的空間特性，將結構自重與二期恒載轉換為質量。特征向量采用 Lanczos方法求解，計算階數為前100階，表1列出該橋前10階自振特性。

從上述分析結果可知，全橋第一階振型為全橋縱飄，且振型質量貢獻率達到86.97%，該振型對縱橋向影響較大。

2.2 反應譜分析

基于設計資料，橋位處地震烈度為Ⅷ度，按照Ⅸ度設防。場地土類型為中硬土，場地類別為Ⅱ類場地，特征周期為0.35 s。基于《鐵路工程抗震設計規范》GB50111—2006(2009版)，考慮多遇地震和罕遇地震兩種地震烈度情形，其基本水平地震加速度分別為0.14 g和0.64 g，反應譜圖形如圖2所示。計算中振型的組合方式采用CQC組合。

表1 結構自振特性(前10階)

圖2 地震反應譜

由彈性反應譜分析可知，多遇地震作用下，在縱向地震工況下墩頂最大縱向位移為0.013 m，橫向地震工況下墩頂最大橫向位移0.007 m;罕遇地震作用下，在縱向地震工況下墩頂最大縱向位移為0.057 m，橫向地震工況下墩頂最大橫向位移0.033 m。

3 靜力彈塑性分析

3.1 彈塑性模型的建立

以往震害資料表明，絕大多數橋梁震害主要源于下部結構的破壞，因此本文重點關注地震作用下橋梁墩柱的非線性行為。在彈塑性地震反應分析中，橋墩的恢復力模型確定是最基本的一環。使用有限元軟件MIDAS Civil 2010對橋墩模擬時，需要輸入模擬塑性鉸的非線性單元骨架曲線參數。本文采用彎矩—曲率關系定義的非線性分布式鉸模型，同時考慮軸力—彎矩交互影響，采用多軸鉸本構P—M—M模型。

首先通過Imbsen Software公司開發的專業軟件XTRACT對橋墩截面進行了彎矩—曲率分析和軸力—彎矩相互作用分析。在上部結構自重作用下，橋墩截面的軸力—彎矩相互作用如圖3所示，圖中擬合計算結果與美國ACI規范折減計算結果相同。

圖3 橋墩截面的軸力—彎矩相互作用

由上述相互關系可以確定出構件屈服面，通過軸力來計算屈服彎矩。將相關參數輸入MIDAS Civil 2010，兩個方向的彎矩和屈服彎矩滿足Bresler公式

式中，Mnx，Mny為截面 x，y方向的彎矩值;Mmax為給定軸力作用下的屈服彎矩;α決定曲面形狀，折線形取1，橢圓形取2。

在靜力彈塑性分析中，側向加載模式較為關鍵。考慮到橋墩構件沿高度方向分布較為均勻，且底部最為薄弱，本文采用加速度常量加載模式，將荷載以慣性力的形式分布作用于結構。側向力按照縱橋向和橫橋向兩種工況分別施加，采用位移控制法，每種工況計算步驟數為100，同時分析中考慮了P-delta效應。

3.2 能力譜分析

能力譜方法是靜力彈塑性分析中較常采用的方法，其基本思想是建立兩條相同基準的譜線:一條是由荷載—位移曲線轉化的能力譜曲線，另一條是由加速度反應譜轉化的ADRS譜(亦稱需求譜曲線)，將兩條線放在同一個圖中，兩曲線的交點定義為目標性能點，依此判斷結構抗震性能。

由于我國橋梁規范缺乏相關的規定，參考美國ATC-40推薦方法，同時參照《鐵路工程抗震設計規范》規定反應譜求取目標性能點，基本流程如下:

1)首先由靜力彈塑性分析求得基底剪力和墩頂位移的關系曲線;

2)將Pushover分析曲線轉化為能力譜;

3)依據規范規定的反應譜建立彈性需求譜，將能力譜與彈性需求譜繪制在同一圖中，獲知初始性能點;

4)計算性能點上的等效阻尼及有效阻尼，利用有效阻尼建立彈塑性需求譜，并獲得彈塑性需求譜與能力譜，即新的性能點;

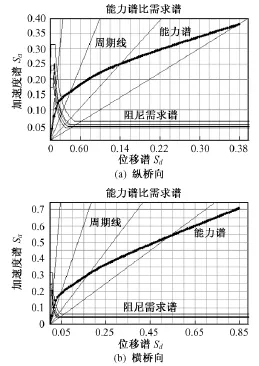
圖4 Ⅸ度多遇地震下橋墩能力曲線

在多遇地震下，縱橋向性能點為 Sa=0.122 6，Sd=0.015 5，經轉化公式得墩底剪力為 Vb=5 927 kN，墩頂位移 u=0.012 m;橫橋向性能點為 Sa=0.124 8，Sd=0.021 6，經轉化公式得墩底剪力為 Vb=4 567 kN，墩頂位移u=0.007 m。結構達到性能點狀態時橋墩構件尚在彈性范圍內。

在罕遇地震下，縱橋向性能點為 Sa=0.225 5，Sd=0.105 6，經轉化公式得墩底剪力為 Vb=10 900 kN，墩頂位移 u=0.083 m;橫橋向性能點為Sa=0.242 1，Sd=0.104，經轉化公式得墩底剪力為Vb=8 858 kN，墩頂位移 u=0.037 m。結構達到性能點狀態時橋墩墩底進入塑性狀態。從墩頂縱橫向位移反應來看，在罕遇地震下縱橋向彈塑性位移較彈性反應譜分析結果大45.61%，橫橋向彈塑性位移較彈性反應譜分析結果大12.1%。

總之，能力譜曲線與需求譜曲線均產生交點，說明該橋滿足Ⅸ度罕遇地震下結構抗倒塌要求。

5)重復以上過程，直至性能點上的位移與加速度響應滿足允許誤差。

基于上述流程，本文計算了該橋在多遇地震和罕遇地震作用下縱橋向與橫橋向橋梁響應。經過Pushover分析將能力曲線、需求曲線以及反應譜曲線按照A-D格式畫在同一張圖中，如圖4與圖5所示。

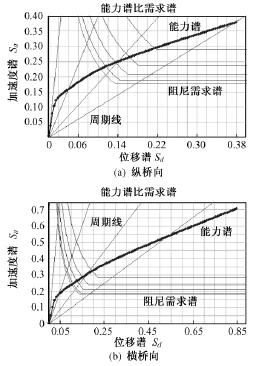
圖5 Ⅸ度罕遇地震下橋墩能力曲線

4 結語

靜力彈塑性分析方法是近年來發展較快的抗震性能評估方法，該方法既能對結構在多遇地震下的彈性設計進行校核，也能確定結構在罕遇地震下潛在的破壞機制，從中找出相對薄弱環節，設計者可以依此局部加強或修復。

［1］中華人民共和國鐵道部.GB50111—2006 鐵路工程抗震設計規范［S］.北京:中國鐵道出版社，2009.

［2］卓衛東.橋梁延性抗震設計［M］.北京:人民交通出版社，2001.

［3］王克海.橋梁抗震研究［M］.北京:中國鐵道出版社，2007.

［4］北京金土木軟件技術有限公司.Pushover分析在建筑工程抗震設計中的應用［M］.北京:中國建筑工業出版社，2010.

［5］邱順東.橋梁工程軟件 MIDAS Civil常見問題解答［M］.北京:人民交通出版社，2009.