鐵路雙線連續鋼桁梁橋豎向有載自振頻率研究
任劍瑩,李文平,蘇木標
(1.石家莊鐵道大學工程力學系,石家莊 050043;2.石家莊鐵道大學土木工程學院,石家莊 050043;3.石家莊鐵道大學大型結構健康診斷與控制研究所,石家莊 050043)
1 概述
列車上橋后,由橋梁恒載以及作用在橋梁上的活載一起確定的結構固有自振頻率稱為有載自振頻率。當作用在橋梁上活載激勵力的頻率——強迫振動頻率與橋梁的有載自振頻率吻合時,將發生共振現象[1]。文獻[2]中也指出:當列車以一定速度勻速通過橋梁時,具有相同長度的多輛車輛的軸重荷載對橋梁的動力作用相當于一個周期性荷載,如果這個周期性荷載的頻率的整數倍與橋梁某一豎向有載自振頻率相等時,車-橋系統將出現豎向共振現象,且共振峰值將隨列車速度的提高而增大。
本文將在文獻[3]的基礎上,推導鐵路雙線連續梁橋的豎向有載自振頻率的計算公式,并計算2列20輛相同參數的提速客車同時通過雙線連續鋼桁梁橋時,車-橋系統的豎向有載自振頻率,得出一些有益的結論。
2 鐵路雙線連續梁橋豎向有載自振頻率計算公式推導
2.1 車-橋系統計算模型
設列車自橋梁左側上橋通過橋梁時(t時刻),列車的第KL到第ML個輪對在橋上,車-橋系統的計算模型如圖1所示。同樣設列車自右側上橋通過橋梁時(t時刻),列車的第KR到第MR個輪對在橋上,計算模型如圖2所示。兩相鄰車輛間的聯接器設為鉸接;每輛車有4個軸,車體理想化為具有沉浮自由度和點頭自由度的剛體;轉向架的質量平均分配給車體和4個輪對;車輛的兩系豎向懸掛彈簧看作串聯線性彈簧,剛度系數用等效剛度系數代替[4];各個輪對與鋼軌始終保持接觸,保證輪對的豎向位移與相應位置的橋梁的撓度始終保持一致。車輛的計算模型如圖3所示。
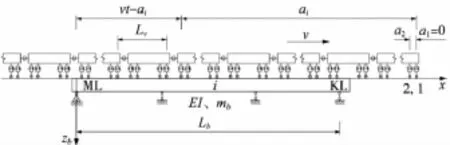
圖1 列車自左側上橋時車-橋系統計算模型
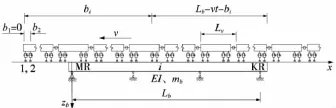
圖2 列車自右側上橋時車-橋系統計算模型

圖3 車輛計算模型
2.2 車-橋系統振動方程
由達朗貝爾原理和車輛的計算模型可得出每輛車的振動方程為[2]
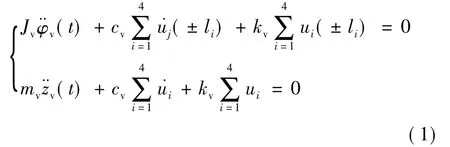
其中:ui為車輛第i軸懸掛彈簧的變形;kv、cv分別為車輛每一軸懸掛彈簧的等效剛度系數和等效阻尼系數;Jv、mv分別為車體的點頭慣性矩和質量;φv、zv分別為車體的點頭位移和沉浮位移;li的意義見圖3所示。
橋梁的振動方程為
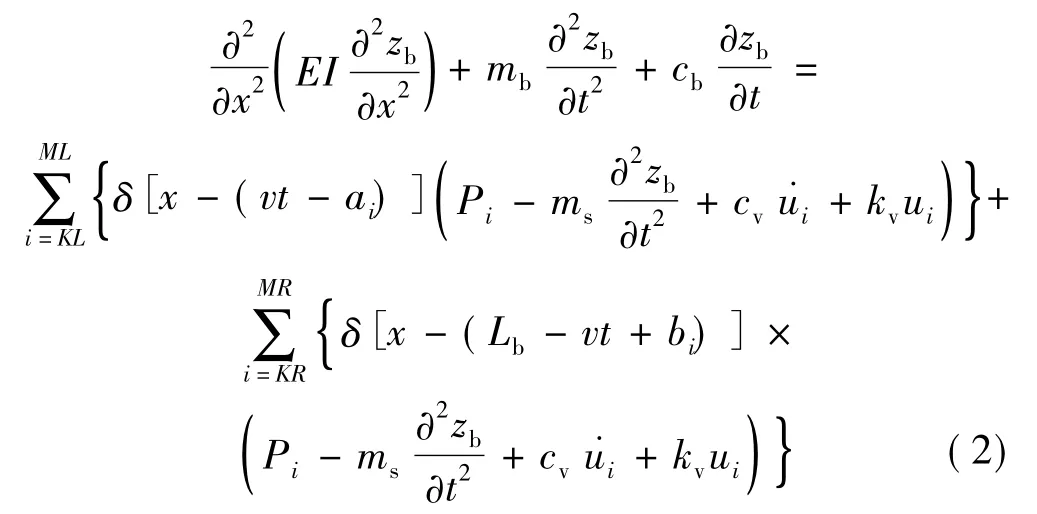
其中:EI、mb和cb分別為橋梁的豎向抗彎剛度、單位長度質量和阻尼系數;Pi為列車第i輪對的靜軸重;ms為列車第i輪對的簧下質量;cv、kv分別為列車第i輪對懸掛彈簧的等效阻尼系數和等效剛度系數;ai、bi分別為左側上橋列車和右側上橋列車的第i輪對距第1輪對的距離(列車最前端的輪對為第1輪對);ui為列車第i輪對懸掛彈簧的變形;v為列車的行駛速度;δ(x-η)是 Dirac函數。
將式(1)和式(2)聯立,可得車-橋系統的振動方程。由陣型疊加法,整理后可得車-橋系統的質量矩陣和剛度矩陣,再由Jacobi方法計算出車-橋系統的豎向有載自振頻率,具體求解方法詳見文獻[3]。
3 鐵路雙線栓焊下承式連續鋼桁梁橋豎向有載自振頻率計算
3.1 計算結果
先計算橋梁的前5個豎向無載自振頻率及其相應的陣型。由于本文只研究橋梁的豎向振動,故橋梁的有限元計算模型等效為一個豎向平面內的計算模型,采用平面桿單元,主桁每兩個結點間的桿件為一個單元,單元的剛度和質量均為等效剛度和等效質量,所有結點均為鉸接,全橋共計93個桿單元,如圖4所示。

圖4 3×64 m單線鐵路栓焊下承式連續鋼桁梁橋計算模型
當2列有20輛相同參數的提速客車分別以160 km/h的速度自橋梁的兩端同時上橋,通過3×64 m雙線鐵路栓焊下承式連續鋼桁梁橋時,自列車的第一輪對上橋時開始計時,計算得到該橋第1、第2、第3、第4、第5豎向有載自振頻率,由于篇幅所限本文僅列出了前3個豎向有載自振頻率隨時間變化的曲線,如圖5~圖7所示。
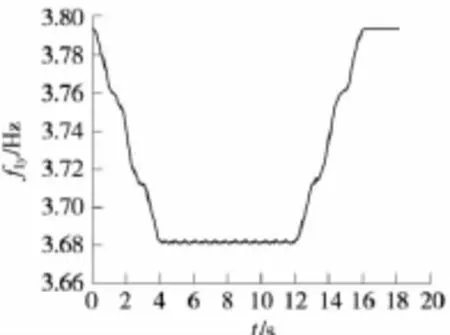
圖5 鐵路雙線連續鋼桁梁橋第1豎向有載自振頻率
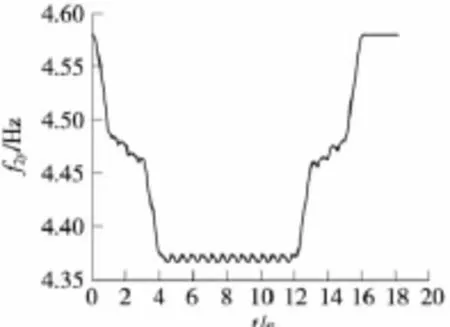
圖6 鐵路雙線連續鋼桁梁橋第2豎向有載自振頻率
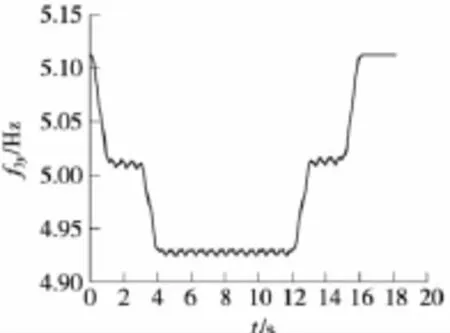
圖7 鐵路雙線連續鋼桁梁橋第3豎向有載自振頻率
3.2 結果分析
通過對該3跨雙線連續鋼桁梁橋的計算,得出與文獻[3]和文獻[6]相似的結論:列車自橋梁兩端同時上橋時,橋梁的豎向有載自振頻率就開始逐漸減小;當橋上滿布車輛時,橋梁的豎向有載自振頻率開始呈周期性變化;當列車開始下橋(由車輛滿布全橋到車輛逐步出橋)時,橋梁的豎向有載自振頻率開始逐漸增大,直至列車全部離開橋梁,橋梁的豎向有載自振頻率恢復到豎向無載自振頻率。
由圖5~圖7可見,變化曲線在下降階段和上升階段,有一個周期變化的階段。該階段是2列列車開始會車,恰好橋上滿布車輛時,和兩列列車錯車后,開始下橋時,豎向有載自振頻率的變化規律,在圖6和圖7中比較明顯。
表1列出了該連續梁橋的前5個豎向有載自振頻率的變化范圍及相應的豎向無載自振頻率值。同時列出了文獻[3]的結論。由表1及圖5~圖7可見,3×64 m鐵路雙線下承式連續鋼桁梁橋的豎向有載自振頻率與豎向無載自振頻率比較,偏差值都比相同跨度單線橋的偏差大,雙線最大偏差為6.042 5%,單線最大偏差為3.260 4%。雙線有載自振頻率的平均值和單線有載自振頻率的平均值相差不多,最大差值為0.166 9 Hz。雙線橋梁豎向有載自振頻率周期變化的范圍比較小,最大差值為0.013 7 Hz<0.1 Hz,因此鐵路雙線連續鋼桁梁橋的豎向有載自振頻率可以取其平均值代替。
4 結論
通過以上計算和分析,得到以下幾點結論:
(1)所得鐵路雙線連續鋼桁梁橋的豎向有載自振頻率的變化規律與簡支梁橋[6]以及單線鐵路連續鋼桁梁橋[3]的豎向有載自振頻率的變化規律相似。
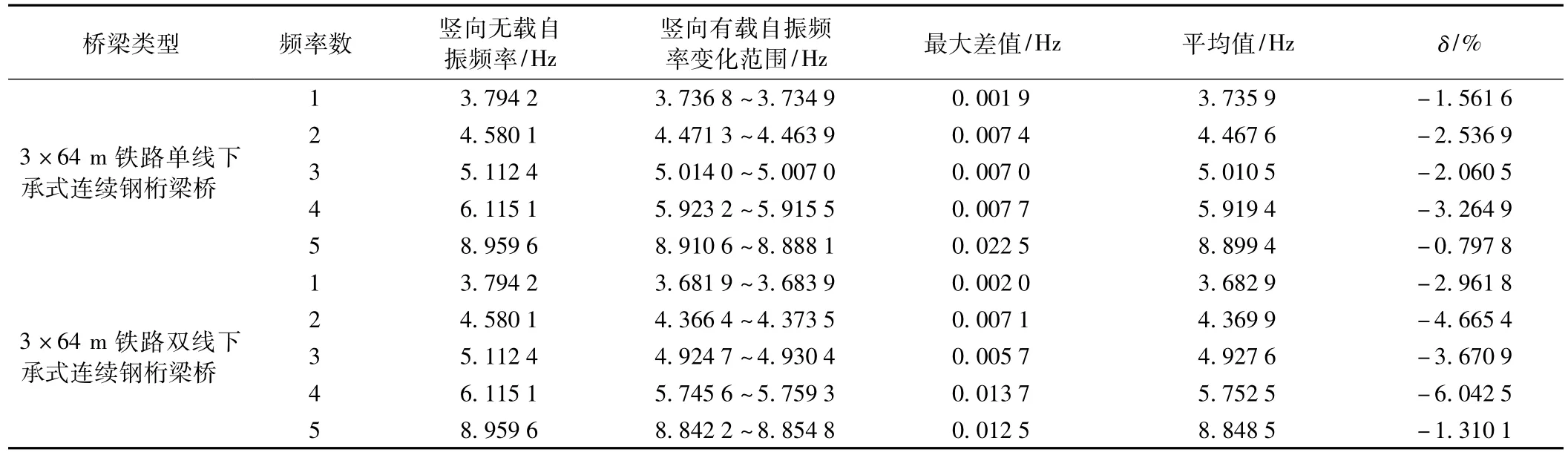
表1 鐵路連續鋼桁梁橋豎向有載自振頻率概況
(2)3×64 m鐵路雙線下承式連續鋼桁梁橋的前5個豎向有載自振頻率偏離其豎向無載自振頻率的差值最小為1.310 1%,最大為6.042 5%,因此,在實際應用時,必須計算橋梁相應的豎向有載自振頻率值。
(3)該雙線連續鋼桁梁橋滿布車輛時,豎向有載自振頻率呈周期性變化,但是變化幅度比較小,最大僅為0.013 7 Hz。因此,實際計算橋梁的豎向有載自振頻率時,可取其平均值代替。
[1]中華人民共和國鐵道部.鐵運函[2004]120號 鐵路橋梁檢定規范[S].北京:中國鐵道出版社,2004.
[2]Li Jianzhong,Su Mubiao.The resonant vibration for a simply supported girder bridge under high-speed trains[J].Journal of Sound and Vibration,1999,224(5):897-915.
[3]任劍瑩,蘇木標,李文平,梁濱波.鐵路連續梁橋豎向有載頻率研究[J].鐵道學報,2005,27(5):111-116.
[4]王福天.車輛動力學[M].北京:中國鐵道出版社,1983.
[5]蔣存煜.有限元基礎[M].北京:清華大學出版社,1984.
[6]蘇木標,李建中,梁志廣.鐵路簡支梁橋豎向有載頻率研究[J].鐵道學報,2001,23(2):76-80.

