混凝土性能預測及配合比優化系統Compos的設計與實現*

陳斌，劉西軍，張曉悅，陳曉東，劉國華

（1. 浙江水利水電專科學校，杭州，310018；2. 中國水電顧問集團華東勘測設計研究院，杭州，310014；3. 浙江大學建筑工程學院，杭州，310058）

1 引言

在給定原材料品種、質量及配合比的情況下，混凝土性能（包括強度、工作性和耐久性）具有唯一對應值，因此必然是可預測的。通過建立各種線性或非線性數學模型，使預測精度得到一定保證，則可用于混凝土配合比設計和生產質量控制等各個方面，是混凝土工程的基礎性工作之一。傳統的混凝土性能預測方法以水灰比定則（保羅米公式）為代表，其認為可塑性混凝土的抗壓強度完全受水灰比的控制，而與其他因素無關。近年來，由于混凝土不斷向高強、高性能化發展，成分不斷復雜，水灰比定則已不完全適用[1]。因而發展出各種調整方法。然而，最直接的混凝土性能預測，仍在于以原材料用量及質量為自變量，通過合適的數學模型，直接推求混凝土性能，已被證明比以各種比率指標（如水膠比、砂率、漿骨比等）為自變量推求混凝土性能更為有效[2]。筆者基于國內文獻公開發表的613組配合比，采用逐步線性回歸和支持向量機等方法，建立混凝土性能預測模型；繼而采用線性規劃的單純形法、粒子群算法建立配合比優化模型，最終集成為Compos混凝土性能預測及配合比優化專家系統。系統同時提供了按《規范》（JGJ55-2000）設計配合比和大體積混凝土溫度場分析功能。

預測、優化變量的選取見表1、表2。

2 混凝土性能預測模型的建立

2.1 線性逐步回歸模型

多元線性回歸是最簡單、最直接的變量相關性統計分析方法，具有物理意義明確、確定性強等優點。由于混凝土性能預測模型的自變量數量較多，可能并非所有的自變量都與因變量有顯著關系，換言之，部分自變量的作用可以忽略，其加入甚至可能降低模型的預測準確性。因而產生了如何從大量可能相關的自變量中挑選出對因變量有顯著影響的部分自變量的問題。逐步回歸分析方法應運而生，其基本思想是：將變量逐個引入，引入變量的條件為偏回歸平方和經檢驗是顯著的，同時每引入一個新變量后，對已選入的變量逐個檢驗，將不顯著變量剔除。這樣保證最后所得的變量子集中的所有變量都是顯著的，經若干步后，可得“最優”變量子集。有關逐步線性回歸方法的具體算法可參考相關文獻[3]，本文不贅述。Compos系統的多元逐步線性回歸界面，如圖1所示。

表1 預測、優化模型的可選自變量

表2 預測、優化模型的可選因變量

2.2 BP人工神經網絡

線性回歸模型雖然具有簡單、直接的優點，但擬合能力有限。若混凝土性能與各自變量間存在非線性關系，則需采用非線性預測模型。最常規的非線性模型當屬多項式擬合。根據泰勒定理，當泰勒級數的項次趨向無窮時，可以任意精度擬合任何函數。但是經驗表明，多項式擬合計算效率較低，但自變量數量較多時，耗時量相當大，且實際選用的項次不可能過多。近年來，人工神經網絡模型（主要為BP人工神經網絡）受到較多關注。所謂BP人工神經網絡，就是以輸入單元為自變量，輸出單元為因變量、網絡單元間的連接權值和閾值為調整參量，按最小誤差原則逐步反饋修正而使網絡達到最佳模擬狀態的一種數學算法。其拓撲結構如圖2所示[4]。

圖1 Compos系統的混凝土性能線性回歸分析界面

圖2 BP神經網絡示意

BP神經網絡的主要參數為隱含層（中間層）單元數。合適的隱層單元數選擇是一個比較復雜的問題，最佳的隱層單元數與輸入、輸出單元數，訓練集樣本數均有關系，目前尚無成熟的理論方法，基本上依賴經驗選定。隱層單元數過少，訓練達不到應有精度，容易出現“欠擬合”；隱層單元數過多，則易出現“過擬合”。筆者經過大量試驗，發現隱層單元數輸入樣本數的1/2（9個），預測精度基本已達到最優。考慮輸入、輸出層單元數的變化，基本認為隱層單元數取10，通常情況下均能適用。

為了控制過擬合，筆者進一步提出了一種“誤差跟蹤策略”，即：首先進行第一次網絡訓練和預測，以其預測誤差作為最優誤差的初始值。而后網絡每訓練一次，立即對預測樣本組進行預測，若預測誤差小于初始值，則取其為最優值并記錄發生位置，如此不斷重復計算，直至網絡訓練誤差或訓練次數達到預定值為止，見圖3。從圖上看，預測相對誤差過程線開始上揚的A點，即為訓練截止點，超過該點，網絡訓練即進入過擬合狀態。

2.3 支持向量機模型

BP人工神經網絡具有較強的非線性擬合能力，但實踐表明，其過擬合控制能力較差。所謂“過擬合”，即指模型過度擬合樣本的個別甚至錯誤信息，而偏離了對整體規律的把握。支持向量機模型（SVMs）是一種基于統計學習理論的新型算法，其建立在統計學習理論的VC 維理論和結構風險最小原理基礎上，能有效抑制過擬合，被普遍認為優于人工神經網絡[5,6]。

圖3 過擬合狀態示意

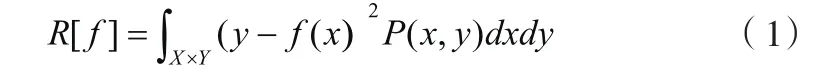
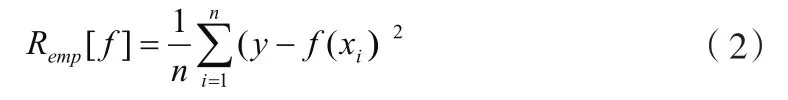
根據大數定律，式(2)只有當樣本數n趨于無窮大且函數集足夠小時才成立。這實際上是假定最小二乘意義的擬合誤差最小作為建模的最佳判據，結果導致擬合能力過強的算法的預報能力反而降低。為此，SLT用結構風險函數 ][fRh代替 ][fRemp，并證明了 ][fRh可用下列函數求極小而得：

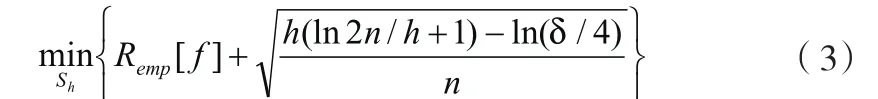
此處n為訓練樣本數目，Sh為VC維空間結構，h為VC 維數，即對函數集復雜性或者學習能力的度量。1-δ為表征計算的可靠程度的參數。

SLT要求在控制以VC維為標志的擬合能力上界（以限制過擬合）的前提下追求擬合精度。控制VC維的方法有三大類：1）拉大兩類樣本點集在特征空間中的間隔；2）縮小兩類樣本點各自在特征空間中的分布范圍；3）降低特征空間維數。一般認為特征空間維數是控制過擬合的唯一手段，而新理論強調靠前兩種手段可以保證在高維特征空間的運算仍有低的VC維，從而保證限制過擬合。

對于分類學習問題，傳統的模式識別方法強調降維，而SVM與此相反。對于特征空間中兩類點不能靠超平面分開的非線性問題，SVM采用映照方法將其映照到更高維的空間，并求得最佳區分二類樣本點的超平面方程，作為判別未知樣本的判據。這樣，空間維數雖較高，但VC維仍可壓低，從而限制了過擬合。即使已知樣本較少，仍能有效地作統計預報。

對于回歸建模問題，傳統的算法在擬合訓練樣本時，將有限樣本數據中的誤差也擬合進數學模型了。針對傳統方法這一缺點，SVR采用“ε 不敏感函數”，即對于用f (x)擬合目標值y時時，即認為進一步擬合是無意義的。這樣擬合得到的不是唯一解，而是一組無限多個解。SVR方法是在一定約束條件下，以取極小的標準來選取數學模型的唯一解。這一求解策略使過擬合受到限制，顯著提高了模型的預報能力。

3 混凝土配合比優化模型

3.1 單純形法優化混凝土配合比

當混凝土性能預測模型為線性方程，則可采用線性規劃的單純形法進行配合比優化。以1m3混凝土的成本最低為優化目標，以混凝土的設計強度、工作性或耐久性指標為約束條件，優化的數學模型表示如下：

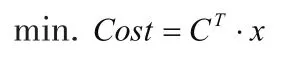
式中， A = [ aij]m×n為線性約束方程組的系數矩陣；為線性約束方程組的右端項矩陣；x = [x ,x...x]T12n為原材料的用量；C =[c1,c2...cn]T為不同原材料的價格；m為約束條件數量，n為自變量數量。

單純形法通過從可行域的一個極點出發，先判斷該點是否是極小點，如是，則運算結束；否則沿能使目標函數下降的方向搜索，抵達下一個極點；繼續執行這一過程，直到獲得最優點為止。其基本過程包括求基本可行解，換基、轉軸運算等。有關單純形法的原理和計算過程可參見文獻[7]。圖4和圖5為采用單純形法優化混凝土配合比的參數設定及計算結果界面。

圖4 Compos系統優化配合比的參數選擇界面

圖5 Compos系統優化混凝土配合比的結果輸出界面

3.2 粒子群算法優化混凝土配合比

粒子群優化算法或稱微粒群算法（PSO）是1995年Russell Eberhart和James Kennedy提出的[8]，PSO源于人工生命理論和鳥類和魚類的群集行為，是一種基于群體智能的優化技巧。與其他進化類算法相似，PSO也采用“群體”與“進化”的概念，同樣也是依據個體（粒子）對環境的適應度大小進行操作，所不同的是粒子群算法不像其他進化算法那樣對于個體使用進化算子，而是將每個個體看作是在多維搜索空間中沒有體積和重量的粒子，以一定的速度飛行搜索，并按照個體的飛行經驗和群體飛行經驗動態地調整飛行的速度，經若干代的并行搜索趨近最優解。現考慮如下的優化模型：

其中，f ( X)為定義在D維歐氏空間 ED的區域S上的實函數，設 N為群體規模，為粒子i的當前位置，為粒子i的當前飛行速度，fitnessi= f (Xi)為粒子i的適應度值，其中 i = 1 , 2 ,L,N.記pbesti和分別為粒子i曾經達到的最佳適應度值及其對應于D維空間中的位置，gbest和 Pg=(pg1, pg2,L,pgD)T分別為群體中所有粒子曾經達到的最佳適應度值及其對應位置。基本粒子群算法采用的進化方程（動態調整規則）是：

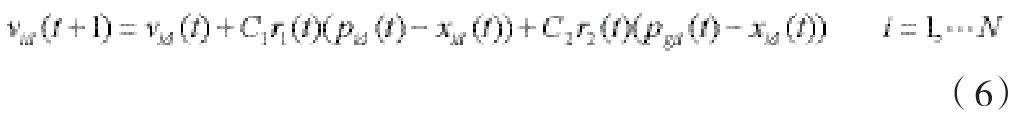
式中，下標i表示第i個粒子，d表示粒子的第d維，t表示第t代，C1,C2為學習常數，分別稱為認知參數和社會參數，通常在0～2間取值， r1～∪(0,1)和r2～∪(0,1)為兩個相互獨立的隨機數。

為了改善算法的收斂性能，1998年Y.Shi和R.C. Eberhart在速度進化方程中引入慣性權重w[9]，即：

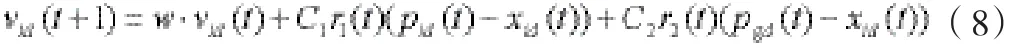
采用（6）（7）式的稱基本粒子群算法，采用（8）（7）式的稱標準粒子群算法。

取混凝土各種原材料的用量為“粒子”，可建立上述的PSO優化模型。優化模型中，需考慮強度、工作性、耐久性等約束條件。可采用適應度與違反度雙值控制法。將約束條件與目標函數分離，讓每個粒子都具有兩個函數值，一個對應于目標函數的適應度值，一個對應問題的約束條件，反映粒子關于約束的違反程度。

粒子的優劣將由上述二個函數按一定規則決定：

a.當二個粒子i和j都可行時，比較它們的適應度值fitness i和fitness j，適應度值小者為優；

b.當二個粒子i和j都不可行時，比較它們違反度值voilationi和 vo ilationj ，違反度值小者為優；

c.當粒子i可行，粒子j不可行，如果voilalionj＞e則粒子i為優；若voilalionj＜e則比較它們的適應度值fitness i和fitness j，小的粒子為優。有關PSO算法的具體過程可參見有關文獻[10]。圖6是PSO算法優化混凝土配合比的過程。

4 Compos系統的集成

以配合比數據庫為平臺，筆者集成了混凝土性能預測與配合比優化系統。系統同時包含了按《普通混凝土配合比設計規程》（JGJ55-2011）和《水工混凝土試驗規程》（SL 352-2006）設計配合比，以及基于有限元法的大體積混凝土溫度場分析的模塊。系統框架如圖7所示。

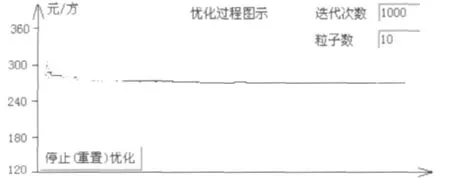
圖6 PSO算法的優化過程

圖7 Compos系統框架

系統同時具有Excel數據導入與導出、試驗調整等功能，方便用戶的整個配合比設計、試驗流程。

[1]陳斌，李富強，劉國華，等. 混凝土配合比的非線性多目標優化研究[J]. 浙江大學學報，2005, 39(1): 16-19.

[2]Dias W P S, Pooliyadda S P. Neural networks for predicting properties of concretes with admixtures[J]. Construction and Building Materials, 2001(15): 371-379.

[3]徐世良主編. C常用算法程序集（第二版）[M]. 北京：清華大學出版社，1996.

[4]劉國華，陳斌等，基于人工神經網絡和Monte-Carlo法的混凝土配合比優化設計研究，水力發電學報[J]，2003（4）：45-53.

[5]S. M. Gupta. Support Vector Machines based Modeling of Concrete Strength[J]. International Journal of Electrical and Computer Engineering, 2008,3(5): 312-318.

[6]崔海霞. 高強混凝土強度預測的支持向量機模型及應用[J]. 混凝土, 2010(5): 49-51.

[7]汪樹玉，劉國華. 系統分析[M]. 杭州：浙江大學出版社，2002.

[8]Kennedy J., Eberhart R.C . Particle swarm optimization [C].In: Proc. IEEE Int. conf. on neutral network,1995,1942-1948

[9]Shi Y., Eberhart R.C. A modified particle swarm optimizer[C]. In: IEEE world congress on computational intellegence,1998, 69-73.

[10]劉華瑩，林玉娥，王淑云. 粒子群算法的改進及其在求解約束優化問題中的應用[J]. 吉林大學學報（理學版），2005（4）：