變電站二次設備全壽命周期費用與可靠性關系模型
黃 莉,張雪松,楊衛星
(1.浙江同濟科技職業學院,杭州 311231;2.浙江省電力試驗研究院,杭州 310014;3.浙江大學電氣工程學院,杭州 310013;4.浙江省電力設計院,杭州 310012)
0 引言
目前,國家電網公司正在全面推進變電站設備的LCC(Life Cycle Cost,全壽命周期費用)管理工作。在設備初始選型階段,將不僅僅考慮其購置成本,還計及運行維護、退役等成本,從全壽命周期費用的角度對設備進行評價。從用戶的角度出發,希望設備可靠性高且全壽命周期費用盡量低,但在實際中,這個目標卻難以實現,因為高可靠性的要求必然帶來廠家的高投入,設備價格也將相應提高。因此,如何在設備可靠性和全壽命周期費用之間進行權衡是目前亟需解決的問題。文獻[1-5]針對變電設備的可靠性問題進行了研究;文獻[6-9]則研究了變電站變壓器、GIS等一次設備壽命周期費用管理問題。這些成果均未對變電站二次設備如何在可靠性基礎上進行全壽命周期成本控制進行系統分析。
本文從分析設備LCC與可靠性關系的模型入手,在保證系統可靠性的前提下,通過讓年平均費用達到最小來實現變電站二次設備LCC的最優化,為解決變電站二次設備管理中存在的問題開辟了一條新途徑。
1 設備壽命周期費用定義及計算方法
設備的壽命周期是指設備從論證開始到退役為止所經歷的全部時期,一般可分為論證、方案、工程研制、生產、使用及退役6個階段。設備的壽命周期費用則是指在設備整個壽命周期內各個階段所需支付的費用總和。電力公司是設備使用者,一般不參與生產和科研,因此,電力公司對設備進行全壽命周期費用分析時,按照二次設備壽命周期的運行規律,將設備標準運行狀態及關鍵控制點作為全過程管理的重點,依據LCC理論并根據變電二次設備的相關費用支出情況構建相應的計算模型:
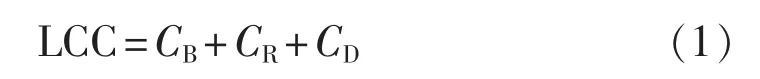
式中:LCC為全壽命周期費用;CB為購置費,包括采購費用和安裝時花費的運輸、人工、調試等費用;CR為運行維護費,即為了保證設備正常運轉而發生的費用,包括運行費用以及在壽命期內檢修、維護、試驗等所需要的材料費、人工費和交通費等維護費用;CD為退役處置費用,即變電設備退役后拆除、運輸等費用。
設備的全壽命周期管理就是在滿足可靠性、安全性的前提下,以LCC最小為目標的管理方法。因此,LCC的估算是全壽命周期管理工作最基礎、最重要的工作。
目前,LCC的估算方法有工程估算法、類比估算法、參數模型估算法和專家判斷估算法[10]。
(1)工程估算法
工程估算法是最傳統的LCC估算法,依據LCC的分解結構,對設備在購置、使用維護及報廢等不同階段的各個環節和過程中需支出的費用加以測算,逐項疊加后得出整個系統各階段的總費用,最后集成為壽命周期費用,其特點是詳盡、具體、繁瑣、費時,但精度較高,可達90%。
(2)類比估算法
類比估算法一般用于新研制設備與現有設備具有類似功能、且其結構和性能特征與現有設備又是可比的情況。將新研制設備與現有設備(已有準確費用數據和技術資料)在技術、使用與維護方面進行比較,分析兩者的異同點及其對費用的影響,根據經驗判斷求出新研制設備相對于現有設備的費用修正方法,再計算出新研制設備的費用估計值。
該方法適用于研制的早期階段,在不能采用參數估算法和工程估算法時使用,也經常用于驗證參數估算法的估算結果。利用該方法可以估算壽命周期費用或某項主要費用和單元費用,或者某一個主要分系統或設備的費用。
對現有系統各有關費用作有針對性的修正(即考慮到配置上的差異),即可得到新系統所需費用。但是這種修正主要憑借經驗,誤差較大,所以很少獨立使用。
(3)參數模型估算法
參數模型估算法是利用同類設備歷史統計數據導出的數學關系來估算新設備費用的方法,即利用匯集起來的具有類似用途的硬件與軟件的現有大量數據庫,僅用系統少量設計參數或特征量來表達費用的參數方程,然后把一系列費用估算關系方程有機地編排和組合在一起,構成費用模型,通過計算機處理,即可得出相應的費用。
費用估算關系式可能很簡單,也可能很復雜,即可反映設備研制、生產和使用維護費用,又能反映這些費用的個別部分或幾個部分的組合。因此,系統級或分系統級均可采用此法來估算費用。
參數模型估算法特別適用于設備招標計劃的早期階段。該方法要求輸入的參數少,估算快,費用省,因此有助于分析各種選型方案變化時的費用。其估算精度取決于基本費用數據的質量和預期的外推精度。但是,由于新的設備在技術、生產工藝、采購策略、生產率或工業基礎等方面都將發生很大變化,不易把歷史統計數據調整到統一的基礎上,因此系統級的估算精度不高,而分系統級由于有更多的技術數據輸入,其精度預計可以達到很高。
(4)專家判斷估算法
專家判斷估算法是由專家根據經驗估算設備壽命周期費用的方法,可由多個專家分別獨立估算,再加以綜合,以提高估算精度。一般在數據不足或沒有足夠的統計樣本以及難以確定參數費用的關系式時使用,或用于輔助其它估算方法。
2 二次設備可靠性與LCC關系模型
系統可靠性對LCC有很大影響,主要體現在:購置費CB依賴于可靠性指標的高低,可靠性指標的高低對運行維護費CR產生重大影響,主要體現在對CB和CR的影響呈現兩種相反的趨勢。可靠性的提高即產品成本提高,導致CB不斷提高,而CR卻大幅度降低;可靠性較低,即CB降低,但CR卻要升高。設備退役處置費則可認為是一常數。因此LCC將呈“浴盆”曲線,如圖1所示,因而存在一個可靠性優化區域,即圖1中R1與R2之間的區域。可靠性并不是越高越好,而應以LCC最低為目標,因此,在考慮可靠性與LCC關系時,應遵循合理性、方便性的原則。選用故障率λ作為參與因子,式(1)中認為CD是與可靠性無關的常數,因此主要考慮購置費CB和運行維護費CR與λ的關系。
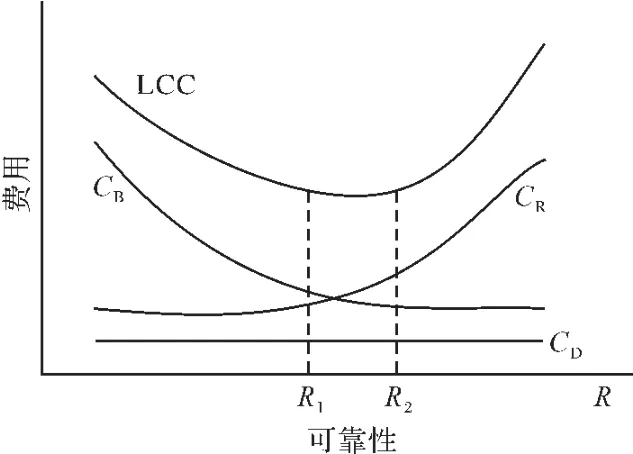
圖1 壽命周期費用LCC與可靠性R關系曲線示意圖
對某指定設備來說,當考慮可靠性對相關費用的影響時,設其它說明性的變量與可靠性不相關,作為常數處理,即:
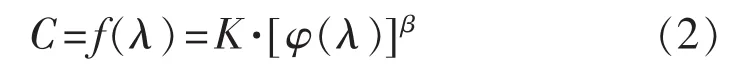
式中:C為相關費用;λ為故障率;K,β與λ無關,是待定系數。
設購置費 CB=fB(λ)=K1·[φB(λ)]α, 如果要求故障率很低,廠家的設計、研制及試驗的費用將增加,設備的購置成本很高如果只要求很低的可靠性,則購置費會很低,也就是說 fB(λ)應滿足:
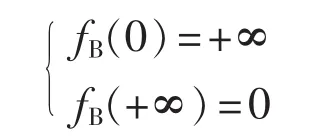
顯然fB(λ)為減函數, 且K1, α 為與 λ 無關的正常數,因此φB(λ)≥0且為關于可靠性R的增函數, 也滿足根據函數論,φB(λ)滿足上述兩個條件的最簡單的形式為:
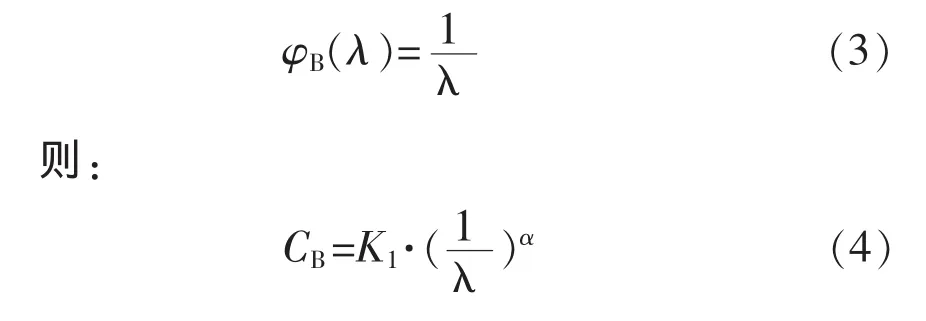
對于檢修費用CR,情況則有些不同,它不僅與 λ有關,而且和時間t有關,即CR=fR(λ)·t=K2·[φR(λ)]β·t。fR(λ)應滿足:
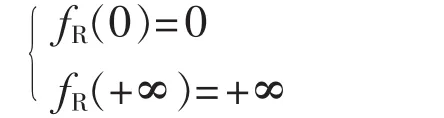
φR(λ)≥0且為關于 λ 的增函數,K2, β 為與λ無關的正常數,其滿足條件的最簡單形式為:
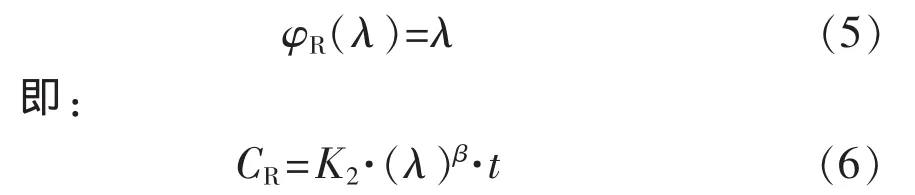
將式(4)、 (6)代入式(1)得:
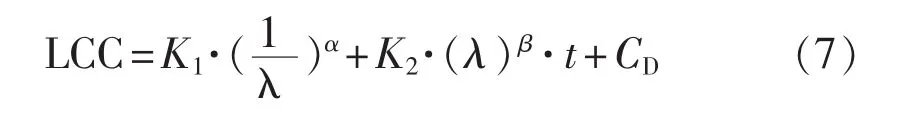
式(7)中K1, K2, α, β 是待定系數, 可通過回歸分析來確定,主要步驟為:
(1)可靠性數據、全壽命周期費用的收集、分析整理。
(2)將式(7)的非線性方程線性化,主要方法是兩端取自然對數,方程轉化為關于lnK1,lnK2,α,β的線性方程。
(3)利用可靠性數據、壽命周期費用數據,通過線性回歸方法(如最小二乘回歸)來給出K1,K2,α,β的值。
3 設備壽命周期費用優化
由式(7)可知,設備的LCC是與MTBF(平均無故障時間)和服役時間t都相關的函數,而在考慮LCC最優時,還需要將其歸算到同一時間間隔下才有意義,因為服役時間越長,其LCC越高,但平均到每年,其平均費用不一定高。因此,本文引入年平均費用YC的概念,通過實現YC的最優,來實現LCC的最優化。
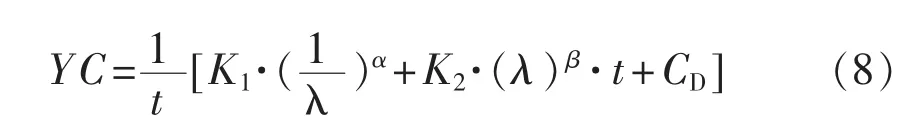
首先考察在給定λ時,YC隨時間t的變化規律, 由式(8)得:
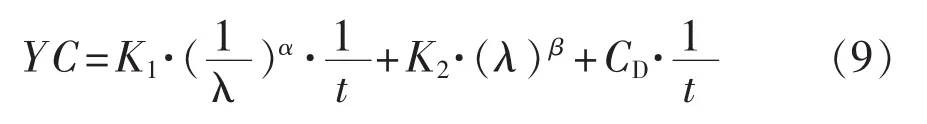
可見,此時YC是關于t的減函數,也就是說,在設備壽命范圍內,服役時間越長,年平均費用越低。電子產品的壽命取決于其薄弱部件的壽命,以保護產品為例,典型設計壽命一般都≥10萬h,不考慮技術升級的因素時,其服役時間可選擇接近其壽命值。
當設備的服役周期t0給定時,考察YC隨時間λ的變化規律,對式(8)兩邊關于λ求導,得:
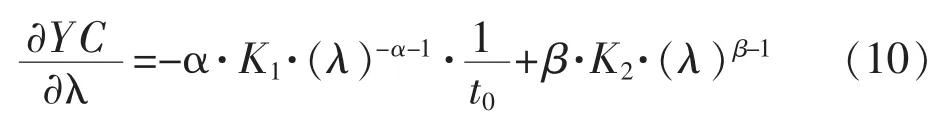
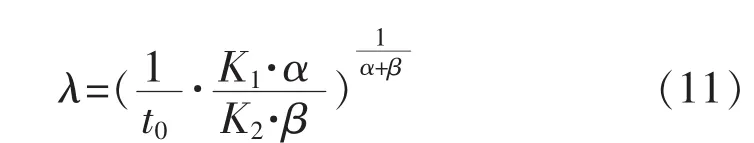
轉化成平均無故障工作時間:
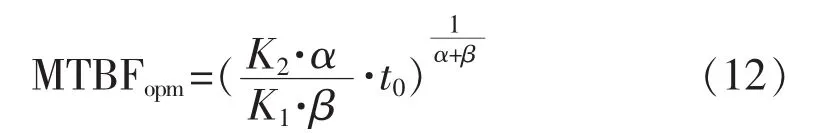
在實際應用中,求得的MTBFopm不一定符合一次系統對二次設備可靠性要求,此時則應按系統要求確定MTBF,以保證可靠性前提下的費用最優。
4 結語
在深入分析設備壽命周期費用與可靠性關系的基礎上,給出了一種可靠性與LCC的關系模型,并通過引入平均年費用YC,對故障率一定和服役時間一定兩種情況下的費用優化作了深入探討。本文給出的模型在實際應用中還會遇到較多的問題,需要在實踐中不斷完善。
[1]張雪松,吳志力,程曉東,等.基于環境應力分析的變電站二次設備可靠性評估[J].浙江電力,2009(3):16-19.
[2]邱仕義.電力設備可靠性維修[M].北京:中國電力出版社,2004.
[3]郭永基.電力系統及電力設備的可靠性[J].電力系統自動化,2001,33(17)∶53-56.
[4]丁堅勇,鄧瑞鵬,李江.發電設備的檢修策略及可靠性管理研究[J].電網技術,2002,26(3)∶72-75.
[5]殷天雷,史進淵.發電設備可靠性與設備檢修管理策略的研究[J].動力工程,2001,29(4)∶1303-1305.
[6]郭基偉,謝敬東,唐國慶.電力設備管理中的壽命周期費用分析[J].高壓電技術,2003,29(4)∶13-15.
[7]姚明,陳紅兵,李莉華,等.全壽命周期成本(LCC)方法在500 kV地下變電站GIS采購中的應用[J].中國電力,2008,41(8)∶32-34.
[8]姜益民,馬駿.變壓器的全壽命周期成本分析[J].變壓器,2006,43(12)∶30-34.
[9]李璐.電力一次設備全壽命周期組合化管理模式及實施[J].供用電,2009,26(2)∶13-15.
[10]李向榮,郭廣生,徐宗昌.武器裝備壽命周期費用估算方法研究[J].科技導報,2008,26(15)∶84-88.

