隨機振動功率譜再現自適應控制算法研究

關廣豐，王海濤，熊 偉

(大連海事大學 機械工程系，大連 116026)

振動模擬實驗的目的在于考核設備或試件在振動環(huán)境下保持其原有性能的能力，為試件的性能測試和技術改進提供實驗依據。試件在工作環(huán)境中經受的振動形式大多為隨機振動，振動信號的頻率不局限在確定的頻率點上，其特征經常用功率譜密度等統(tǒng)計特性描述［1］。隨機振動功率譜再現實驗的目的，就是在實驗臺上高精度再現實測的功率譜密度信號(即參考譜信號)，研究試件的結構可靠性和操縱可靠性［2］。

液壓振動模擬系統(tǒng)負載能力大，易實現低頻大位移、大推力的振動激勵，常用于大型工程結構或試件的模型及實物的振動模擬試驗［3，4］。但受系統(tǒng)頻寬的限制及液壓系統(tǒng)非線性因素的影響(如油溫變化等)，僅采用伺服控制很難滿足隨機振動實驗的精度要求。為了提高控制精度，更準確地再現參考譜信號，需要通過振動控制對驅動信號進行迭代補償，減小響應信號的功率譜密度與參考譜信號的差別，形成一種真正意義上的振動閉環(huán)控制［5］。

傳統(tǒng)的隨機振動控制算法大多基于頻響函數的離線辨識結果對驅動譜進行修正，再通過頻域隨機化和時域隨機化方法將功率譜信號轉換為時域信號，驅動平臺運動［6，7］。時域隨機化后生成信號的頻譜存在泄漏現象，在頻率分辨率之間可能產生欠試驗或過試驗，影響系統(tǒng)的控制精度。而且，由于傳統(tǒng)控制算法為離線迭代算法，當實驗過程中系統(tǒng)特性發(fā)生變化時，很難保證實驗的控制精度。

基于自適應濾波理論辨識系統(tǒng)的阻抗特性，并依據實時辨識結果修正驅動信號，將有利于提高隨機振動實驗的控制精度。Karshenas等［8］基于快速塊LMS自適應濾波算法，應用自適應逆控制技術實現了沖擊波形的高精度再現。Groud等［9］應用LMS自適應濾波器設計了電動振動臺隨機振動控制器，并通過仿真驗證了算法的有效性。

LMS算法實現簡單，但收斂速度慢。基于遞歸最小二乘估計的RLS算法可以將自適應濾波算法的收斂速度提高一個數量級。進一步研究表明，RLS算法實際上只是Kalman濾波算法在無激勵線性動態(tài)系統(tǒng)模型假設條件下的一種簡化，基于線性動態(tài)系統(tǒng)狀態(tài)空間模型的Kalman濾波算法更適合于進行系統(tǒng)辨識［10］。因此，研究基于Kalman濾波的隨機振動控制算法有利于進一步提高控制算法的實時性。

本文首先提出基于濾波器設計理論的時域驅動信號生成方法，基于參考譜的信息設計FIR濾波器，通過對白噪聲信號的濾波生成時域驅動信號。然后利用Kalman濾波器辨識系統(tǒng)的阻抗特性，基于自適應逆控制方法對激振系統(tǒng)的輸入信號進行補償，使得系統(tǒng)的響應信號能夠實時再現時域驅動信號，進而實現參考譜的高精度再現。最后通過隨機振動實驗對算法的有效性進行驗證。

1 時域驅動信號生成方法

圖1所示為基于濾波器設計理論的時域驅動信號生成過程原理圖。利用參考譜設計FIR濾波器，通過對白噪聲信號的濾波生成時域驅動信號。

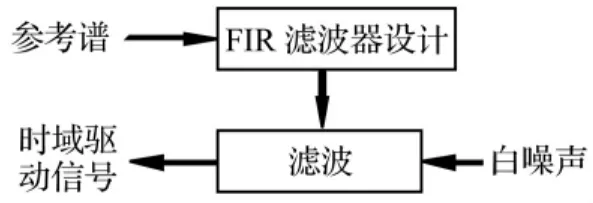
圖1 時域驅動信號生成方法Fig.1 Time domain drive signal generation

定義Gdd(f)為系統(tǒng)輸入信號功率譜密度估計值，Gcc(f)為系統(tǒng)響應信號自譜密度估計值，H(f)為系統(tǒng)的頻率響應函數。由隨機過程理論可知:

式中，上角標H表示復向量的共軛轉置。

取驅動信號為白噪聲信號，則其功率譜密度Gdd(f)可近似看為常數。設Gdd(f)=b，式(1)可簡化為:

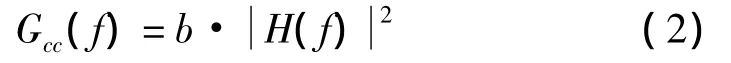
由式(2)可得:

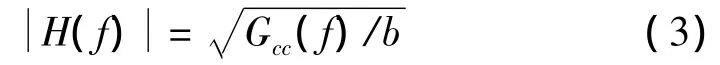
實驗中，設定白噪聲輸入信號的功率譜密度為b，令參考譜信號為Gcc(f)，由式(3)計算所設計的FIR濾波器的幅頻特性。

取線性相位φ作為FIR濾波器的相頻特性，有:

式中，M為FIR濾波器的階數。

已知濾波器的幅頻特性和相頻特性，基于Parks-McClellan方法，通過最小化FIR濾波器頻率特性和期望頻率特性之間的最大誤差，利用Matlab信號處理工具箱中的Remez函數設計等紋波FIR濾波器［11，12］。

利用所設計的FIR濾波器對白噪聲信號進行濾波，生成時域驅動信號。由于白噪聲信號的功率譜均勻分布在整個頻段內，因而大大減小了濾波生成的時域驅動信號的頻譜泄漏現象。

2 自適應阻抗辨識

基于單步預測的Kalman濾波算法辨識振動實驗系統(tǒng)的阻抗特性，利用自適應逆控制技術對系統(tǒng)的輸入信號進行修正，使得系統(tǒng)的響應信號能夠再現參考信號。

2.1 Kalman濾波器

Kalman濾波器基于隨機狀態(tài)空間模型給出了線性動態(tài)系統(tǒng)狀態(tài)向量的最小均方估計。取狀態(tài)向量的估計值為FIR濾波器的權值向量，圖2給出了Kalman濾波器的實現框圖［13］。

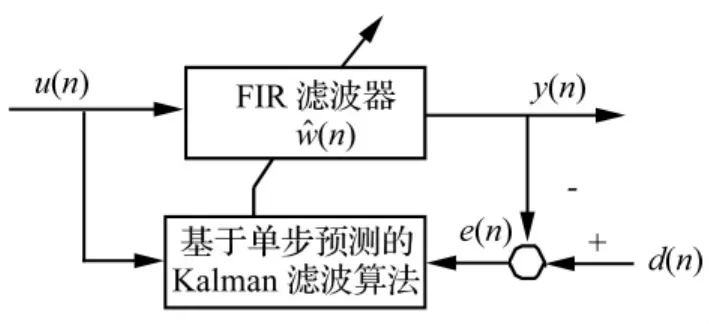
圖2 Kalman自適應濾波器Fig.2 Kalman adaptive filters

圖2中u(n)和y(n)分別為濾波器的輸入和輸出信號，d(n)為期望信號，e(n)為偏差信號，w^(n)為FIR濾波器權值向量的估計值。由圖可知:

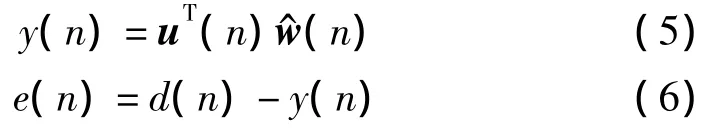
對于線性定常系統(tǒng)，Kalman濾波器的單步狀態(tài)轉移矩陣為常值。由于穩(wěn)態(tài)時FIR濾波器的權值收斂于常數，或處于緩變狀態(tài)，因此取單步狀態(tài)轉移矩陣為單位陣［14］?；跇藴蔏alman濾波算法可得

式中，g(n)為Kalman增益矩陣，K(n)為狀態(tài)估計誤差的相關矩陣，QM為測量噪聲的相關矩陣，Qp為過程噪聲的相關矩陣。基于e(n)和g(n)更新FIR濾波器權值向量的估計值:

式(5)～式(9)給出了基于單步預測Kalman濾波算法的FIR濾波器權值的最小均方估計遞推公式。迭代過程趨于穩(wěn)態(tài)時，FIR濾波器即為u(n)與d(n)之間脈沖傳遞函數的最優(yōu)估計。

2.2 阻抗辨識

激振系統(tǒng)的輸出信號往往存在噪聲。由Kalman自適應濾波器原理可知，將系統(tǒng)輸出信號作為濾波器的輸入信號直接辨識系統(tǒng)阻抗時，無法得到阻抗特性的最優(yōu)估計。而系統(tǒng)輸出信號的噪聲不影響自適應濾波器辨識傳遞函數的精度。因此，基于自適應逆控制原理，首先利用自適應濾波器辨識系統(tǒng)的傳遞函數，再通過辨識傳遞函數的逆得到系統(tǒng)的阻抗特性［15］。圖3給出了基于Kalman自適應濾波器的阻抗辨識方法原理圖。

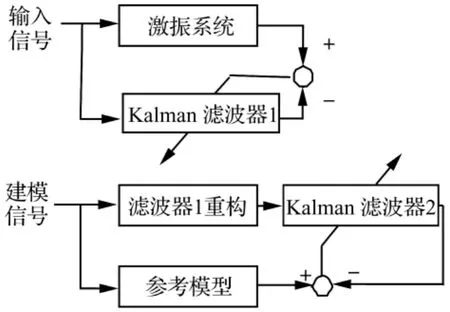
圖3 基于自適應濾波器的阻抗辨識Fig.3 Inverse modeling based on adaptive filters

將激振系統(tǒng)的輸入信號作為Kalman濾波器1的輸入信號，系統(tǒng)的輸出信號作為濾波器1的期望信號，基于單步預測Kalman濾波算法辨識激振系統(tǒng)的傳遞函數。

取限帶白噪聲信號作為建模信號，基于Kalman濾波器1的辨識結果，通過復制濾波器的權值重構濾波器1并對建模信號進行濾波，所得輸出作為Kalman濾波器2的輸入信號。將建模信號經參考模型之后的輸出信號作為Kalman濾波器2的期望信號，基于單步預測Kalman濾波算法辨識Kalman濾波器1的阻抗特性?？芍瑸V波器2的辨識結果為參考模型和激振系統(tǒng)級聯后的阻抗特性。

3 隨機振動自適應控制算法

取延遲環(huán)節(jié)z－m(m為正整數)作為參考模型，圖4給出了基于6自由度運動平臺的隨機振動自適應控制算法原理圖。

圖4中“運動學反解”和“運動學正解”模塊用于在6自由度位姿信號和6路液壓缸信號之間進行相互轉換［16］。

利用參考譜的信息設計FIR濾波器，通過對白噪聲信號濾波生成時域驅動信號。將時域驅動信號作為Kalman濾波器2的建模信號，通過復制Kalman濾波器2的權值重構濾波器2并對時域驅動信號進行濾波修正，所得輸出作為6自由度運動平臺的位姿輸入信號。由2.2節(jié)分析可知，平臺的位姿輸出信號將再現延遲后的時域驅動信號。信號的延遲不改變其功率譜密度，因而使得6自由度運動平臺的響應譜能夠高精度再現參考譜信號。

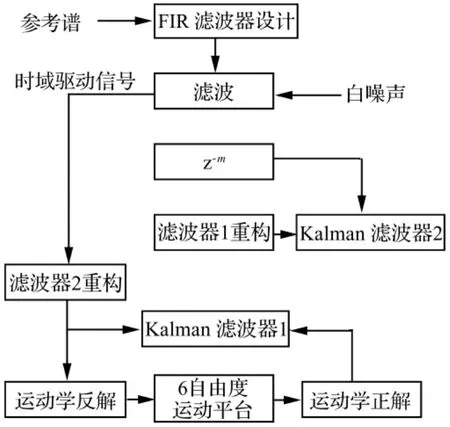
圖4 隨機振動自適應控制算法Fig.4 Random vibration adaptive control

4 實驗研究

為驗證隨機振動自適應控制算法的有效性，在圖5所示6自由度運動平臺Z方向上進行兩組隨機振動實驗。

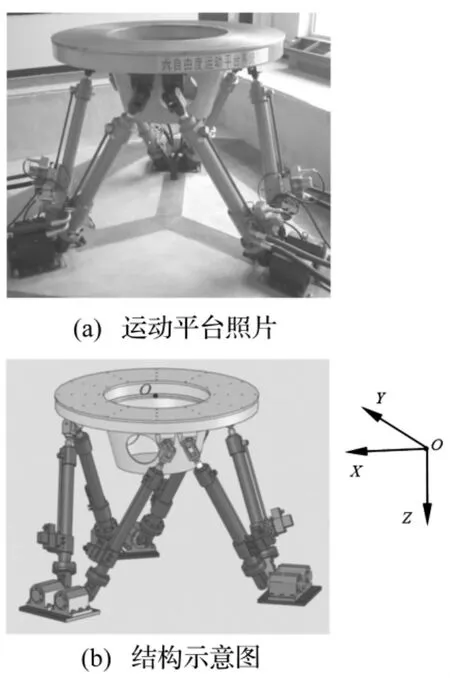
圖5 6自由度運動平臺Fig.5 6 Degree-of-freedom platform

參考譜由兩段組成，在0.1 Hz～20 Hz為平直譜，20 Hz～25 Hz為下降譜，平直譜功率譜密度為7×10－9m2/Hz。取參考譜的±3 dB作為隨機振動實驗控制精度的容差限［17］，實驗一中不修正時域驅動信號，將其直接作為6自由度平臺的位姿輸入信號，測量系統(tǒng)的響應信號。實驗二中采用圖4所示隨機振動自適應控制算法控制平臺運動。兩組實驗中均采用Welch方法估計響應信號的功率譜密度。

圖6給出了參考譜和白噪聲信號經FIR濾波器濾波后所得時域驅動信號功率譜的對比圖。

由圖6可知，經濾波生成的時域驅動信號的功率譜均在參考譜的±3 dB容差限內，表明基于濾波器設計理論的時域驅動信號生成方法是可行的。

圖7給出了兩組隨機振動實驗中的功率譜再現實驗曲線。

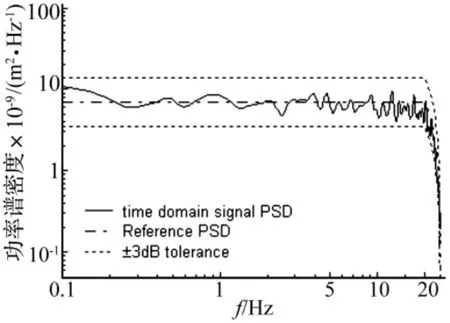
圖6 參考譜與時域驅動信號功率譜Fig.6 PSD of reference signal and time domain drive signal

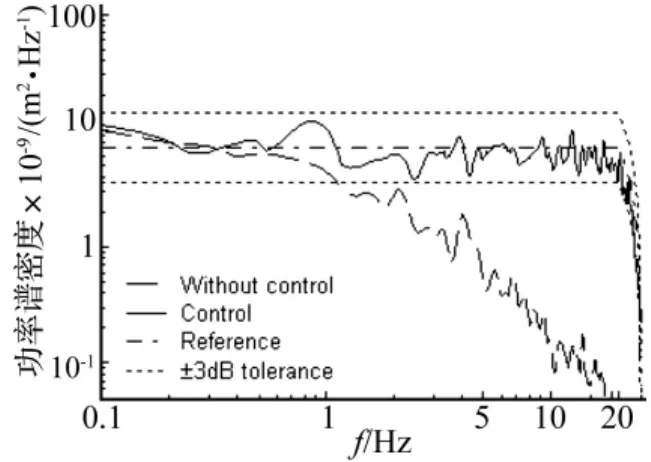
圖7 隨機振動實驗結果Fig.7 Random vibration test results

由圖7可知，無迭代補償時系統(tǒng)的響應譜遠遠超出參考譜的±3 dB容差限，高頻時(20 Hz附近)響應譜衰減甚至超過30 dB。采用隨機振動自適應控制算法時，響應譜在整個頻段內均控制在參考譜的±3 dB容差限內，實現了參考譜的高精度再現。

5 結論

提出了一種基于自適應濾波器的隨機振動自適應控制算法。基于濾波器設計理論將參考譜轉換為時域驅動信號，利用Kalman自適應濾波器實時在線辨識振動實驗系統(tǒng)的阻抗特性，并對時域驅動信號進行濾波修正，通過再現時域驅動信號的方法再現參考譜信號。隨機振動實驗結果表明基于自適應濾波器的隨機振動控制算法能夠有效的拓展系統(tǒng)頻寬，實現參考譜信號的實時高精度再現。

文中參考功率譜信號的頻帶為20 Hz。隨著參考信號頻帶的提高，要求算法的運算周期隨之減小。因此，進一步研究提高隨機振動自適應控制算法收斂性及收斂速度的方法，將有利于高頻參考譜信號的高精度再現。另一方面，設備或試件在實際工作環(huán)境中經受的振動是多維的，在多個軸向上同時存在。因此基于自適應濾波理論的多軸隨機振動實時自適應控制算法也是后續(xù)的研究方向之一。

［1］Edwin A S.Vibration control system［P］.United States，4989158.1991－01－29.

［2］陳章位，于慧君.振動控制技術現狀與進展［J］.振動與沖擊，2009，28(3):73－77，86，200.

［3］韓 強，杜修力，劉晶波，等.多維地震作用下隔震橋梁地震反應(I)——模型結構振動臺試驗［J］.振動與沖擊，2008，27(9):59－65，182－183.

［4］楊志東，叢大成，韓俊偉，等.基于擴展型準牛頓優(yōu)化算法的單軸正弦掃頻振動控制［J］.振動與沖擊，2008，27(3):99－103，112，182－183.

［5］Stroud R C，Hamma G A.Multiexciter and multiaxis vibration exciter control systems［J］.Sound and Vibration，1988，22(4):18－28.

［6］Smallwood D O.Random vibration testing of a single test item with a multiple input control system［C］.Proceedings of the Institute of Environmental Sciences'28th Annual Technical Meeting，USA，Dallas，TX，1982:42－49.

［7］Stroud R C，Hamma G A，Underwood M A，et al.A review of multiaxis/multiexciter vibration technology［J］.Sound and Vibration，1996，30(4):20－27.

［8］Karshenas A M，Dunnigan M W，Williams B W.Adaptive inverse control algorithm for shock testing［J］.IEEE Proc-Control Theory and Applications.2000，147(3):267 －276.

［9］Groud D R，Gupta H O，Agarwal P.Design of random vibration controller using adaptive filtering［J］.International Journal of Recent Trends in Engineering，2009，2(5):75－79.

［10］Sayed A H，Kailath T.A state-space approach to adaptive RLS filtering［J］.IEEE Signal Processing Magazine.1994:18－60.

［11］The MathWorks，Inc.Filter design toolbox:designing advanced filters:optimal filter design solutions.Matlab Help Document［CP/CD］.US，MA:The Math Words，Inc，2002.

［12］McClellan J H，Parks T W.A personal history of the Parks-McClellan algorithm［J］.IEEE Signal Processing Magzine.2005，22(2):82－86.

［13］Haykin S.自適應濾波器原理［M］.第四版.鄭寶玉等譯.北京:電子工業(yè)出版社，2003，369－389.

［14］Qureshi S U H.Adaptive equalization［C］.Proceedings of the IEEE，1985，73(9):1349－1387.

［15］Widrow B，Walach E，Adaptive inverse control-a Signal processing approach［M］.Reissue ed.Hoboken，New Jersey:John Wiley＆ Sons，Inc.，2008，138－144.

［16］張尚盈，趙 慧，韓俊偉.六自由度運動平臺實時控制的正/反解算法［J］.機床與液壓，2003，(3):133－135，123.

［17］JB/T 8288－2001.中華人民共和國機械行業(yè)標準［S］.液壓振動臺.北京:中國機械工業(yè)聯合會，2001.