煤塊沖擊破碎速度研究

劉 瑜，杜長龍，付 林，高魁東

(中國礦業大學 機電工程學院，徐州 221116)

煤塊破碎是煤炭洗選的一個重要生產環節，它可以使原煤更適合洗選加工，也可以使產品煤滿足用戶對粒度的需求［1］。沖擊破碎具有破碎比大和能耗低的優點，同時兼有中碎和細碎的雙重作用，是煤塊破碎的主要方法［2］。為提高沖擊破碎的能量利用率，增加沖擊破碎的生產能力，需要對煤塊沖擊破碎過程進行分析，確定其主要設計參數——沖擊破碎速度的取值范圍。

目前國外學者［3－6］對沖擊破碎的研究多集中于沖擊式破碎機的破碎性能，都沒有對破碎時自由煤塊與沖擊板沖擊碰撞過程進行分析，無法準確獲得破碎所需的沖擊速度。國內已有一些學者進行了沖擊速度的研究，但多是采用數值模擬和計算機仿真方法。房琳等［7］用有限元方法通過MSC.Dytran軟件對板錘沖擊煤塊的過程進行了仿真，得到了沖擊過程中使破碎力損失較小的沖擊速度。LI Fang-wei和 LI Yan-huan等［8］通過LS-DYNA軟件對煤巖沖擊破碎過程進行模擬，得到破碎煤需要的沖擊速度值約為10 m/s。由于煤塊形狀的隨機性和內部結構及材料性質的復雜性，通過計算機建立的沖擊模型對煤塊的形狀、結構等進行了簡化，與實際煤塊存在差異，分析結果的必然與實際情況存在誤差。曾洪茂和周恩普［9］從Hertz的沖擊破碎基本定律出發，推導了沖擊速度的數學表達式，但是在他們的推導過程中沒有考慮破碎的能量損失，因此得到的理論沖擊速度小于實際沖擊速度。

本文將對自由煤塊與沖擊板沖擊破碎過程進行分析，基于非線性接觸模型［10，11］和裂縫假說確定煤塊破碎所需的沖擊速度，并通過煤塊沖擊破碎試驗，修正沖擊速度的理論表達式，得到與煤塊自身物理性質相關的沖擊速度計算模型，為煤塊破碎時沖擊速度的初選提供理論依據。

1 煤塊沖擊破碎速度

1.1 煤塊沖擊過程動力分析

為便于理論分析，首先做如下假設:

(1)煤塊是半徑為R的球體，且在沖擊過程中不發生破碎。

(2)沖擊板為剛性無限大平板，碰撞時不產生變形。

煤塊與沖擊板的沖擊碰撞過程如圖1所示，圖中v1為煤塊的沖擊速度，δ為煤塊沖擊過程中的最大變形量，v2為煤塊反彈后的速度。從圖1可以看出，煤塊與沖擊板的碰撞過程可以分為壓縮和恢復兩個階段，這兩個階段以煤塊變形量最大的時刻為分界點。

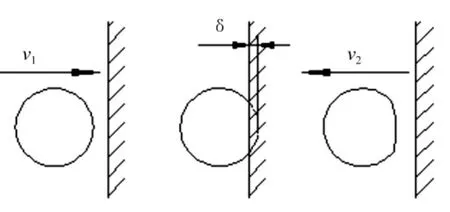
圖1 煤塊沖擊過程分析Fig.1 Analysis of impact for lump coal

煤塊是非線性脆性材料，內部存有裂隙，在碰撞階段裂隙被壓密會產生不可恢復的塑性變形。根據文獻［10］的論述，脆性材料碰撞并且產生塑性變形的應該選擇分段塑變碰撞模型。因此，煤塊和沖擊板的沖擊過程用非線性接觸模型來表示［11］:

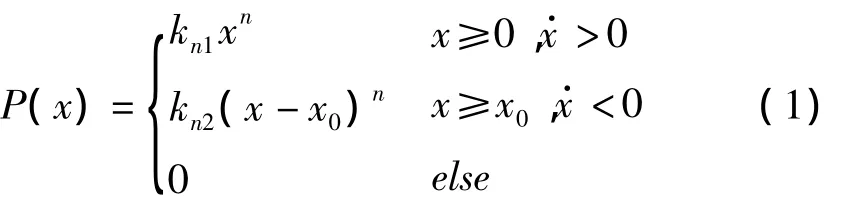
式中:P(x)為接觸力;x為變形量;n為變形量冪次，n=;kn1為壓縮階段的接觸剛度［12］，對于煤塊和沖擊板的沖擊過程有，i=1，2，其中Ei和vi分別為兩接觸體的彈性模量和泊松比，下標"1"表示煤塊，下標"2"表示剛體;kn2為恢復階段的接觸剛度;x0為煤塊的不可逆變形量。

根據壓縮階段能量守恒，可以得到最大變形量xmax和最大接觸力Pmax的表達式:

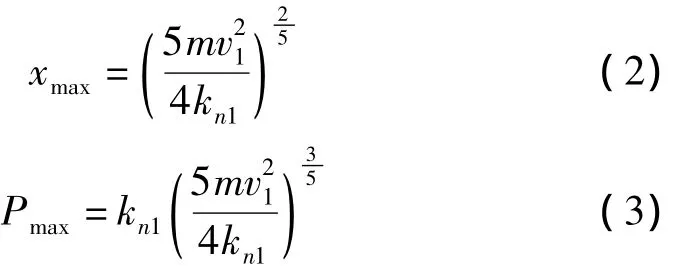
對應的內應力為:

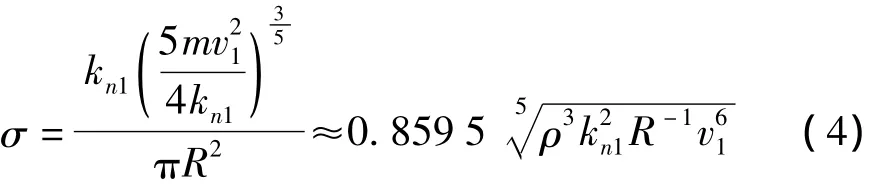
式中:m為煤塊的質量;ρ為煤塊的密度。

1.2 煤塊沖擊破碎速度范圍

煤塊若要發生破碎，必須滿足內應力大于煤塊開始破碎時的極限應力，根據文獻［13］中的分析，煤塊破碎的極限應力為:

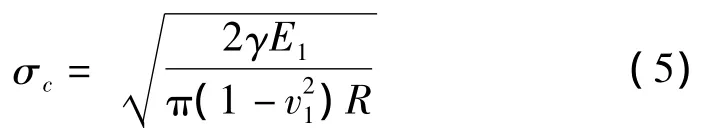
式中:γ為煤塊增加單位表面積所需的表面能。

煤塊沖擊破碎所需要的應力必須滿足σ≥σc，結合公式(4)，可以得到煤塊發生破碎需要的沖擊速度范圍:

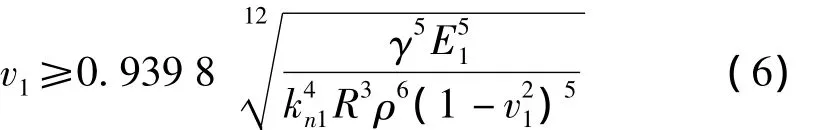
該公式為煤塊發生破碎所需要的最小沖擊速度，當沖擊速度大于該數值時，煤塊才有可能發生破碎。對于煤塊的破碎，人們關心的是破碎后煤塊的粒度，為此需要得到煤塊被破碎到指定粒度所需要的沖擊速度。

1.3 煤塊破碎到指定粒度需要的沖擊速度

常用的煤巖破碎理論有面積假說、體積假說和裂縫假說。由于實際煤塊中存在很多裂隙，適合選擇裂隙假說進行煤塊的沖擊破碎速度計算。

根據裂縫假說將體積為V的煤塊從粒度Dp破碎到粒度dp所需的功耗為:

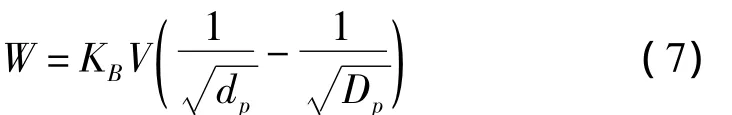
式中:KB為裂縫假說系數，可由試驗得來。

煤塊沖擊碰撞過程中的能量轉化關系有下面兩種情況:

(1)煤塊與沖擊板沖擊但不發生破碎。在這種情況下，煤塊的初始能量——動能，在壓縮和恢復兩個過程中，被內部阻尼所損耗，因此初始的動能主要轉變為阻尼損耗的能量和碰撞后煤塊的動能，阻尼損耗的能量通過恢復系數體現。

(2)煤塊與沖擊板沖擊且發生破碎。在這種情況下，內部阻尼僅在壓縮階段損耗能量，在壓縮結束時煤塊的內應力達到破碎應力，煤塊發生破碎，其初始動能主要轉變為壓縮階段的阻尼損耗能量和使煤塊破碎的能量。

壓縮階段阻尼消耗的能量可以近似認為是壓縮和恢復兩個階段阻尼所損耗的總能量的一半，即:

式中:WYZ為壓縮階段阻尼損耗的能量;WZ為整個沖擊過程阻尼損耗的能量，e為碰撞恢復系數。

沖擊破碎過程中的能量轉化可以表示為:

式中:ET為煤塊的初始能量，ET=12mv21;W為煤塊的破碎能量。

由式(6)～式(7)可得用沖擊破碎方法將質量為m的煤塊由粒徑Dp破碎到粒徑dp所需的功耗為:

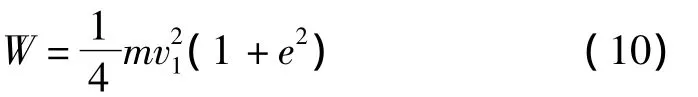
將式(5)代入式(8)，可以得到將煤塊由粒徑Dp破碎到粒徑dp的沖擊速度:

通過式(6)和式(11)可以確定煤塊破碎需要的沖擊速度。對于沖擊式破碎機，其最小沖擊速度可以通過式(6)獲得，如果需要獲得指定破碎粒度的產品煤，則需要結合式(11)來確定具體的沖擊速度。

2 沖擊破碎速度的試驗修正

2.1 沖擊試驗設計

從新汶礦業集團協莊煤礦采集煤塊進行試驗，研究煤塊破碎情況。試驗之前，對煤的性質進行測量，得到試驗煤塊的平均普氏硬度為1.364，抗壓強度為13.5 MPa。

依據重復原則、隨機化原則和區組控制原則將試驗確定為雙因素四水平不等重復試驗，且重復試驗次數原則上不少于7次。結合常用破碎機破碎煤塊的粒度分布情況和式(6)、式(11)理論沖擊速度計算值，確定破碎粒度和沖擊速度的四個水平值，如表1所示。共試驗煤塊235塊，破碎121塊，試驗時量取煤塊破碎前后的最大尺寸，并記錄試驗沖擊速度，為后續研究提供依據。

表1 沖擊破碎試驗影響因素的水平值Tab.1 Level of factors in impact crushing expe riment

2.2 沖擊破碎速度擬合公式

式(9)的等號右邊由常數組成，在進行沖擊速度公式修正時，將式子右邊的前半部分視為一個未知數。式中含有兩個不相關的量，即破碎前后的粒度值，因此必須進行多元回歸分析。

常用的多元回歸分析方法有線性和非線性兩種。通過試算，線性回歸方法得到的估計結果與試驗測量的速度值誤差太大，故采用非線性的多元回歸分析。Matlab中的"nlinfit"函數專門用于非線性的最小二乘數據擬合，通過多次驗證，采用如下形式的非線性模型能夠較好的擬合試驗數據:

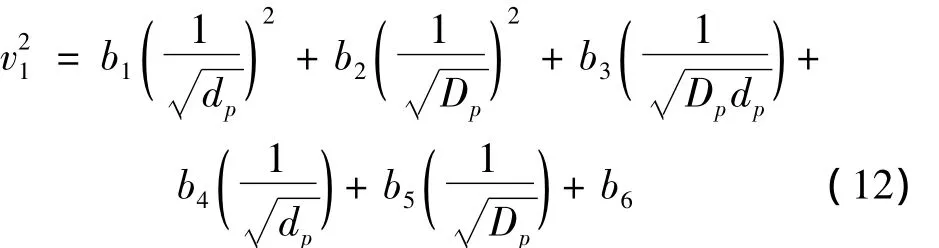
式中:bi為常系數，i=1，2，…，6，可以通過試驗數據獲得。用協莊礦煤塊的破碎試驗數據進行擬合，可以得到適合于該煤礦的擬合系數:

將協莊礦擬合數據繪制曲面并與試驗值對比，如圖2所示。經計算有53.92%的擬合沖擊速度值和試驗值的誤差小于5%，88.23%的擬合值與試驗值誤差小于10%，精度較高。

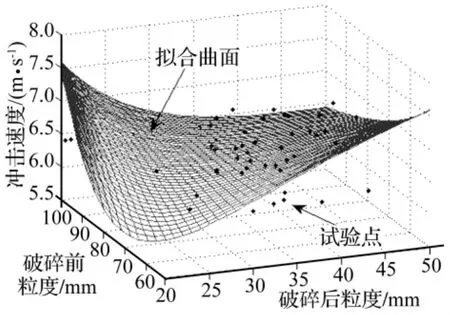
圖2 擬合曲面與試驗散點對比Fig.2 Comparison of fitting surface and experiment points

2.3 沖擊破碎速度公式修正

式(12)擬合精度高，但是結構形式比較復雜，并不適合作為沖擊破碎速度的初選公式，因此要利用試驗數據對理論公式進行修正，得到適合工程應用的沖擊破碎速度初步選擇依據。

式(9)表明沖擊破碎速度是破碎前后粒度的一次函數，經計算實際沖擊破碎速度與理論速度相差不大，因此考慮在理論計算公式上添加修正系數，即:

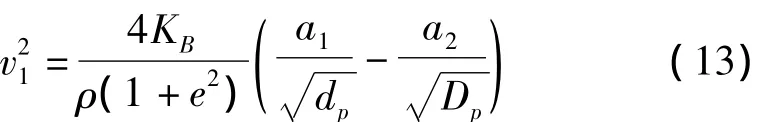
式中:ai為常系數，i=1，2，可以通過試驗數據獲得。結合試驗數據，對于協莊煤礦的煤塊，有a1=0.075，a2=－0.493。

將修正后的沖擊破碎速度理論值與試驗值進行比較，有50%的理論值與試驗值誤差小于10%，70%的理論值與試驗值誤差小于15%，85%的理論值與試驗值誤差小于20%。這表明理論修正公式具有較高的精度，可以作為沖擊破碎速度初選的理論依據。

3 結論

考慮煤塊的脆性以及碰撞過程中的塑性變形，采用分段塑變模型得到了煤塊與沖擊板碰撞過程中的接觸力。以裂縫假說為基礎推導了煤塊沖擊破碎速度的理論公式，并以此為基礎進行了沖擊破碎試驗。通過對試驗數據的分析，得到沖擊破碎速度的試驗擬合公式和理論修正公式。通過兩個公式的比較得出，試驗擬合公式精度很高，但結構形式復雜，可以作為精確破碎的速度選擇依據，理論修正公式能夠滿足工程應用所需的精度要求，且結構形式簡單，適合作為初級破碎時沖擊破碎速度的理論選擇依據。

［1］智玉蓮，韓志強，龐 怡.石料的篩分與破碎［M］.北京:人民交通出版社，1991.

［2］全國煤炭技工教材編審委員會.選煤機械［M］.北京:煤炭工業出版社，2002.

［3］Sadrai S，Meech J A，Ghomshei M，et al.Influ-ence of impact velocity on fragmentation and the energy efficiency of comminution［J］. International Journal of ImpactEngineering，2006，33(1－12):723－734.

［4］Nikolov S.Aperformance model for impact crushers［J］.Minerals Engineering，2002，15(10):715－721.

［5］Nikolov S.Modelling and simulation of particle breakage in impact crushers［J］. InternationalJournalofMineral Processing，2004，74(1):219 －225.

［6］Tavares L M，Carvalho R M.Impact work index prediction from continuum damage model of particle fracture［J］.Minerals Engineering，2007，20(15):1368－1375.

［7］房 琳，王武龍，李曉楠.基于仿真反擊式破碎機破碎力與沖擊速度的研究［J］.礦業快報，2007，457(5):42 －45.

［8］Li Fangwei，Li Yanhuan，Xu Zhenliang，et al.Numerical simulation on the impacting and comminuting of coal based on LS-DYNA［J］.Journal of Coal Science and Engineering，2008，14(4):644－647.

［9］曾洪茂，周恩普.沖擊破碎機沖擊速度、沖擊時間和沖擊力的確定［J］.礦山機械，1994，1:2－6.

［10］秦志英，陸啟韶.基于恢復系數的碰撞過程模型分析［J］.動力學與控制學報，2006，4(4):294 －298.

［11］秦志英，趙月靜，侯書軍.物料沖擊破碎過程的一種非線性力模型［J］.振動與沖擊，2006，25(2):35 －38.

［12］徐秉業.接觸力學［M］.北京:高等教育出版社，1985.

［13］徐小荷，余 靜.巖石破碎學［M］.北京:煤炭工業出版社，1984.