基于模態應力恢復的車架疲勞壽命計算研究

錢立軍 吳道俊 祝安定 章 適

合肥工業大學，合肥，230009

0 引言

汽車零部件疲勞壽命是汽車設計的一個重要目標。已有的疲勞壽命的預測方法有試驗法和CAE技術分析法。采用試驗法，準確性較好，但周期長，費用高。采用CAE技術，可以在汽車開發初期計算零部件的疲勞壽命并進行改進，有利于縮短開發周期、節省開發費用。但是，以往的CAE分析方法中，采用多剛體動力學模型難以獲得準確的零部件載荷譜，雖效率較高，但誤差較大［1］。如何獲取準確的零部件的載荷歷程成為制約CAE疲勞分析精確性的關鍵因素。

本文采用模態應力恢復（modal stress recovery，MSR）方法進行疲勞壽命計算。首先采用有限元分析車架模態信息，對剛柔耦合整車模型進行試驗場路面仿真，利用模態應力恢復（MSR）理論，精確復現車架在汽車運行中所受載荷歷程，從而計算出車架的疲勞壽命。

模態應力恢復方法是CAE疲勞分析中十分有效的方法，能快速獲得很好的疲勞分析結果，達到縮短開發周期和節省費用之目的。

1 基于模態應力恢復的疲勞壽命計算理論及技術路線

1.1 基于模態分析的柔性體動力學求解

在ADAMS柔性體模型中，賦予柔性體一個模態集，柔性體模型的彈性采用模態表示，用模態矢量和模態坐標的線性組合來表示彈性位移［2］。

定義q為柔性模型上任一點的廣義坐標：

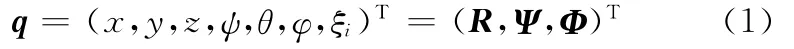
式中，x、y、z為局部坐標系在總體坐標中的位置；ψ、θ、φ為局部坐標系在總體坐標系中的歐拉角；ξi為柔性體的第i階模態位移；R、Ψ為兩坐標系中坐標的矢量表達；Φ為ξi的矢量表達，即模態位移矢量。

由拉格朗日方程表示的模型的動力學方程為

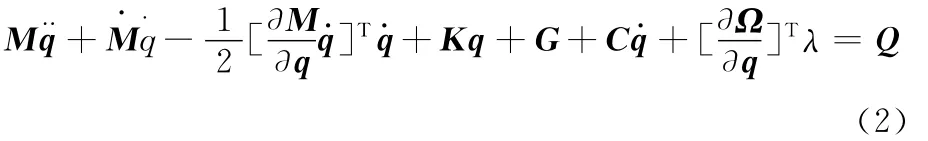
式（2）可簡化為

式中，K、M分別為剛度矩陣和質量矩陣；C為柔體的阻尼矩陣；G為重力；λ為約束方程Ω的拉格朗日乘子；Q為廣義力矩陣；FT為外力矩陣［3］。

由式（2）可解得q，從而可得到式（1）中的模態位移矢量Φ及其各階ξi。

1.2 模態應力恢復

利用有限元（柔性體）模型模態分析得到第i階固有圓頻率ωi、模態振型矢量φi，結合剛柔耦合模型仿真得到模態位移矢量Φ及其各階模態位移ξi，按照模態應力恢復算法可以得到有限元模型上節點的應力σ和反作用力F［4-5］。

模態應力：

式中，σ為節點的應力；Eσ為模態應力矩陣，矩陣中各元素的值與材料彈性模量、泊松比有關，由有限元模型決定。

反作用力：

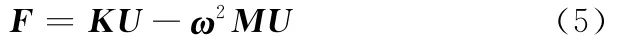
式中，ω為模態圓頻率，為ωi的矢量表達；U為節點位移，是基于模態振型矢量φi和模態位移矢量Φ進行定義的。

由式（4）、式（5）即可分別得到節點應力σ與F的歷程。σ與F即反映出汽車虛擬道路行駛試驗時在零部件上的載荷歷程，可用于零部件的疲勞壽命計算。

1.3 疲勞壽命計算

由于大多數汽車零部件疲勞失效模式是高周疲勞，所以本文中疲勞壽命計算采用適用于高周疲勞的名義應力壽命法（S－N 法）［6］。

按照Miner損傷累積法則，疲勞損傷及疲勞壽命計算式分別為

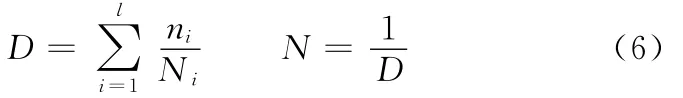
式中，l為變幅載荷的應力水平級數；ni為各應力水平下的循環次數；Ni為各應力水平下的疲勞壽命；D為總疲勞損傷；N為疲勞壽命。

1.4 基于模態應力恢復的車架疲勞分析技術路線

圖1所示為基于模態應力恢復的疲勞計算技術路線圖。

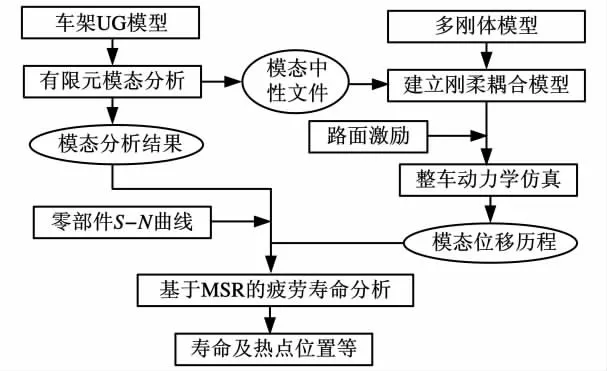
圖1 基于模態應力恢復的疲勞分析技術路線

2 模態分析及整車剛柔耦合模型仿真

2.1 車架模態中性文件的建立及模態分析結果文件的生成

模態分析采用Block Lanczos法，它不僅精確，而且速度較快，不但適用于大型模型，還能提取較多的模態［7］。

建立車架有限元模型時，焊縫采用剛性單元連接，鉚接采用裝配點處單點連接。在對某車架進行模態計算時，由于車架的模態參數只與自身結構有關，計算時將邊界約束條件和外部載荷忽略。

利用有限元軟件建立車架模態中性文件MNF，直接讀取到ADAMS中建立柔性體。在柔性體的轉動中心（與剛性體的連接處）必須有節點存在，此節點在ADAMS中將作為外部節點使用，如果在連接處柔性體為空洞，則需在此處創建一節點，并使用剛性區域處理此節點（外部節點）與其周圍的節點。在車架有限元模型的基礎上建立好的連接點，用于ADAMS整車模型中與其他部件相連接，以Nastran為求解器，得到模態中性文件（．mnf）和Nastran的結果文件Output file（．op2），供后續仿真和疲勞計算使用［8－9］。圖2所示為車架的部分階數的Nastran計算結果。

2.2 建立整車剛柔耦合模型

由于車架模態模型自由度較多，可在ADAMS中檢查MNF的模態振型并對模態進行取舍。取舍標準為：模態頻率要盡可能覆蓋主要的頻率范圍，模態振型要能代表模型主要的變形模式。本文取前15階為有效頻率。

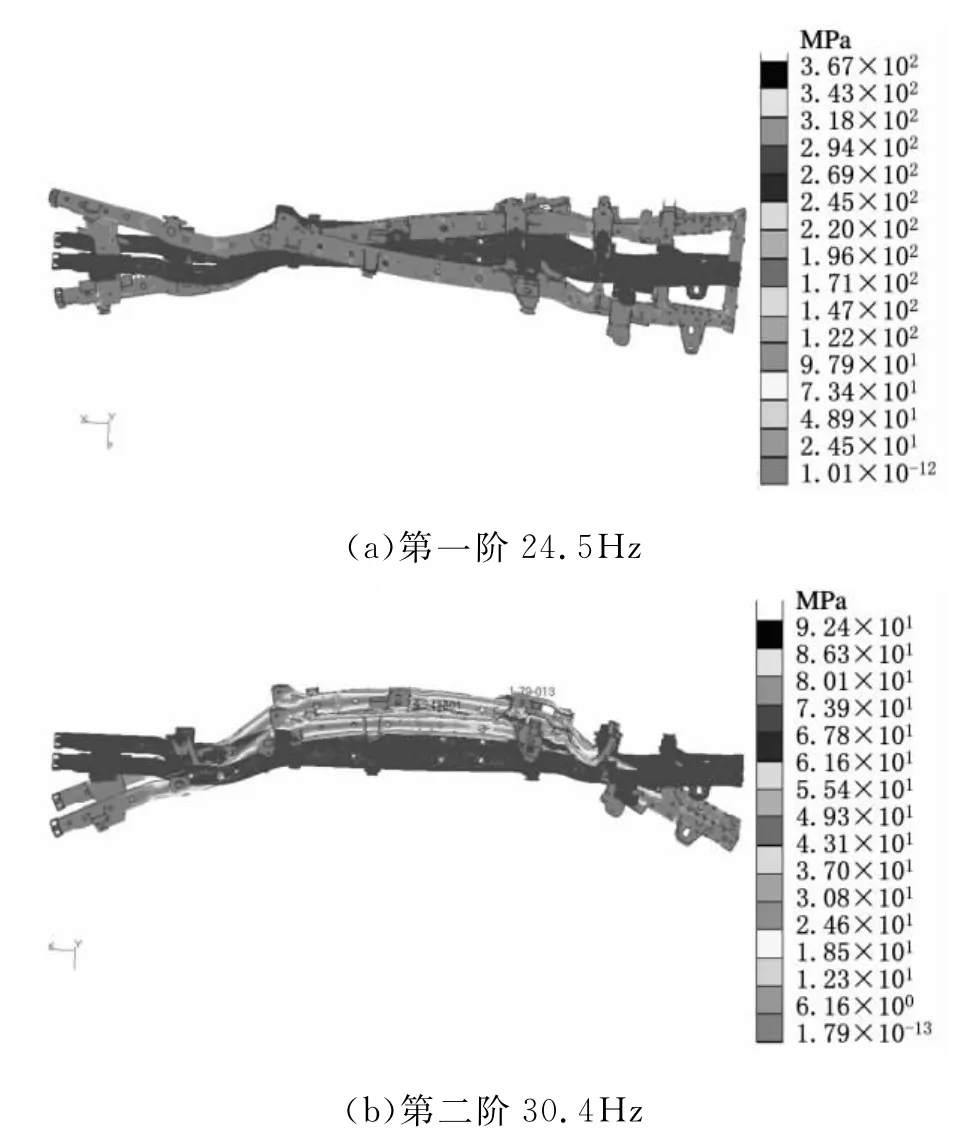
圖2 Nastran模態分析結果

在ADAMS／Car子系統模板中按照整車數據分別建立好整車的轉向系、四輪、前后懸架、前后穩定桿、制動盤、發動機、車身、車架。再直接生成各子系統模型，組裝得到的整車的剛柔耦合模型如圖3所示。模型中，連接處的橡膠塊采用非線性橡膠襯套（bushing）來模擬。

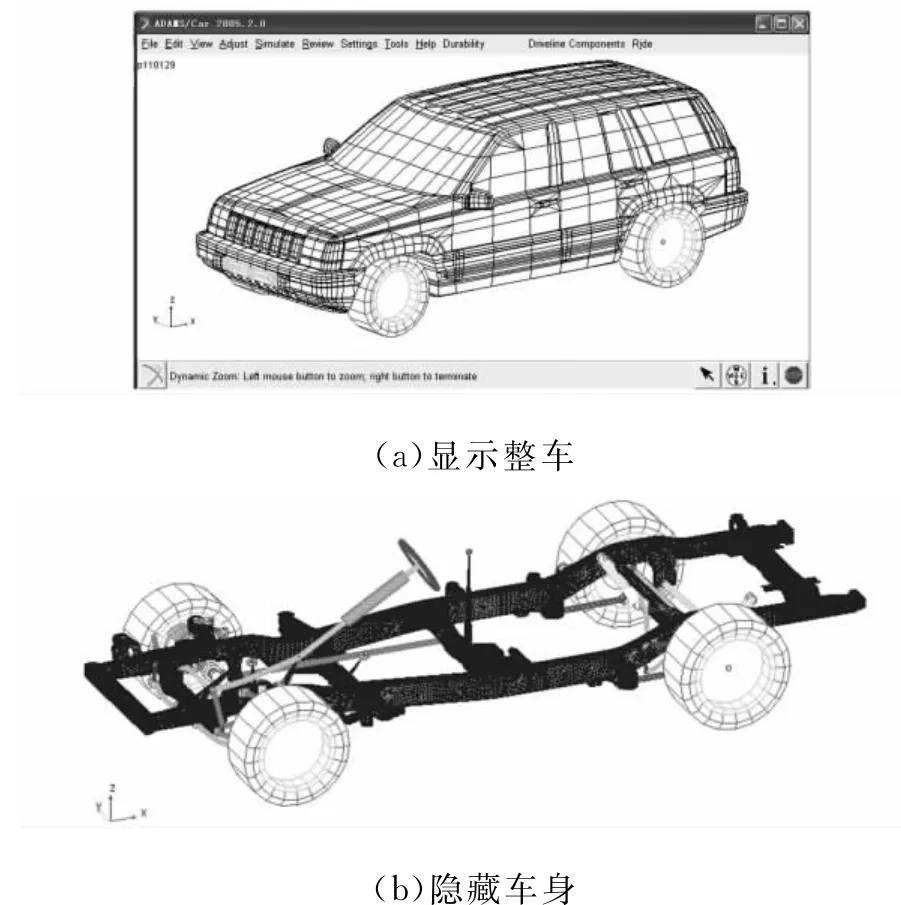
圖3 整車剛柔耦合模型

2.3 整車動力學仿真和模態應力恢復得到車架應力歷程

ADAMS／Car Ride提供了基于四柱試驗臺的各種仿真試驗，即將車輛模型放置到四柱試驗臺上，對試驗臺輸入力或位移的RPC3格式數據文件，從而對車輪施加激勵，實現整車模型仿真試驗，可以用實時采樣的數據模擬汽車行駛在粗糙路面的響應特性。使用ADAMS／Car Ride必須基于一個現存的符合ADAMS／Car規范的模型或子系統數據庫。圖4所示是對2．2節建立的剛柔耦合整車模型進行的強化路面仿真分析。

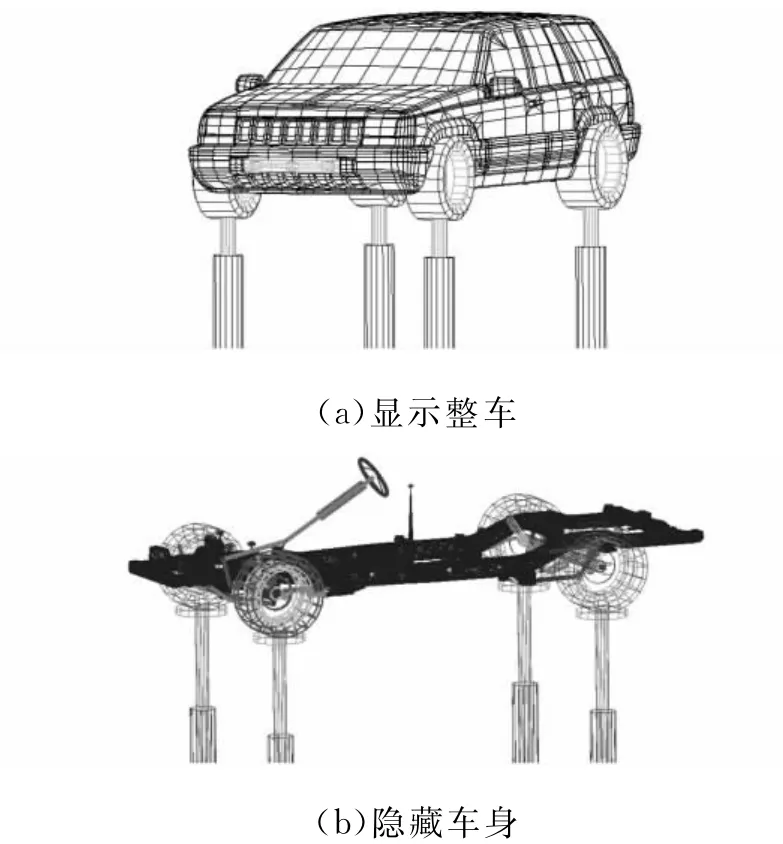
圖4 在四立柱試驗臺上的整車模型

本文采用在試驗場采集的數據整理而得的四輪接觸面位移譜作為四柱試驗臺的輸入，其中一輪位移如圖5所示。模擬試驗時間共計500s左右，對應試驗場一個循環6．56km。

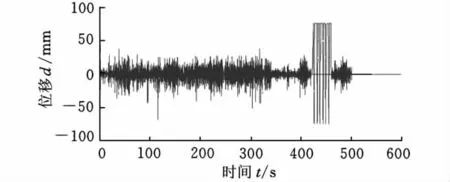
圖5 強化路面右后輪胎接觸面位移譜

由于MNF文件生成的柔性體車架模型中包含模態分析所得的全部模態信息，整車在強化“路面”上“行駛”6．56km（即一個循環）后，柔性車架可以記錄下各階模態位移的時間歷程。由于前6階為零件的剛體模態，將其關閉。值得注意的是，模態位移是無單位標量。圖6所示為其中一些模態位移時間歷程。

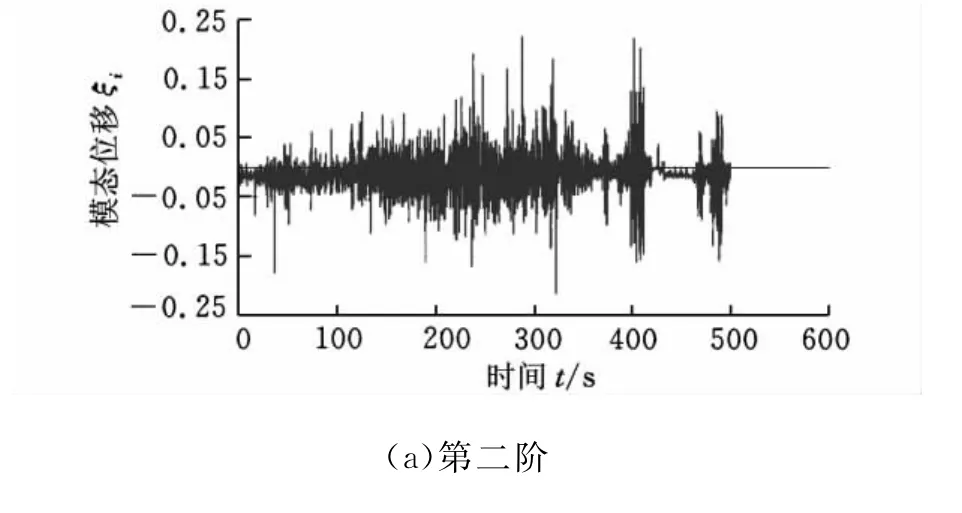
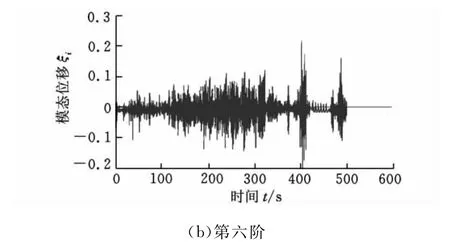
圖6 模態位移時間歷程

按照模態應力恢復理論，在MSC．Fatigue軟件中進行模態應力恢復，即可得到車架每個節點在500s內的應力時間歷程，圖7所示為其中一些點的應力時間歷程。

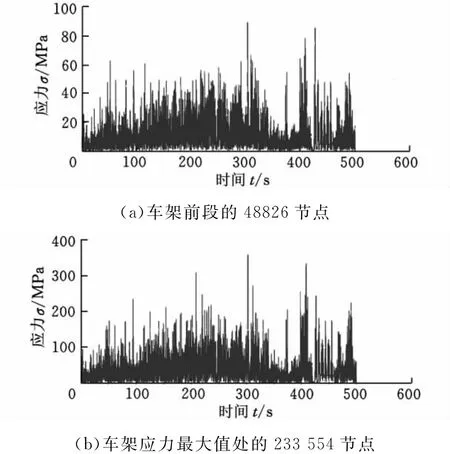
圖7 某些節點的應力時間歷程

在強化路面500s的仿真過程中，最大應力出現在303s時的233 554節點處，最大應力達到379．389MPa。仿真得到的車架應力時間歷程即可用于后期的疲勞計算。

3 車架疲勞壽命分析

準確的S－N曲線是計算正確性的重要因素。本文中車架材料是16Mn鋼。從文獻［10］中16Mn鋼的疲勞性能試驗可得到50%存活率下的疲勞壽命數據，如表1所示，表中S為應力幅值。

表1 16Mn鋼試樣各應力幅值水平下的疲勞壽命［10］

另外，16Mn鋼試樣存活率為50%的疲勞極限是327MPa。

采用冪指數方程描述S－N曲線：

S＝SRI1（N）b

式中，SRI1為y 的插值；b為斜率［6］。

擬合創建材料的S－N曲線如圖8所示，第一個斜率由表1擬合所得，轉折點為疲勞極限值，第二個斜率為零。

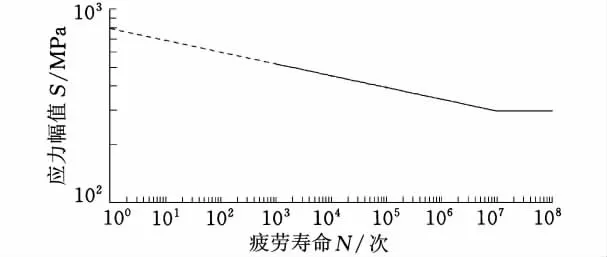
圖8 車架材料的S－N曲線

考慮車架零部件疲勞缺口系數、尺寸系數、表面質量系數、加載方式修正系數，對車架材料的S－N曲線進行修正。將模態分析結果和各階模態位移的．dac文件作為載荷輸入，選擇名義應力法，在 MSC．Fatigue中對車架進行虛擬疲勞分析。采用Goodman圖對平均應力影響進行修正。求得的車架疲勞壽命云圖如圖9所示。

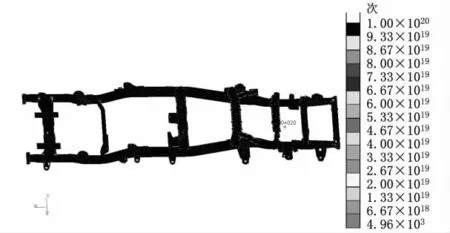
圖9 強化路面車架疲勞壽命云圖

車架最危險點處的循環為4．96×103次，出現在車架最后一根橫梁和縱梁的交接處。已知強化路面一次循環路程，將壽命換算成里程，最危險點的疲勞壽命為32 538km。廠方實際車架在試驗場強化路面的試驗結果為31 050km。

圖10為車架其中三處的仿真結果和道路試驗真實車架試驗結果的對比，從圖中可看出仿真結果與真實車架疲勞壽命較短處（真實車架裂紋處用白線標注）的對應情況。

圖10 仿真結果與道路試驗結果對比（3分圖中上圖為仿真結果，下圖為道路試驗結果）

從試驗結果里程和疲勞壽命危險點的分布上看，仿真結果接近道路試驗結果。

表2列舉出車架最危險點的疲勞壽命計算結果。分析表明，車架的橫梁與縱梁交接處疲勞壽命最低，其余位置整體壽命集中在1019以上。

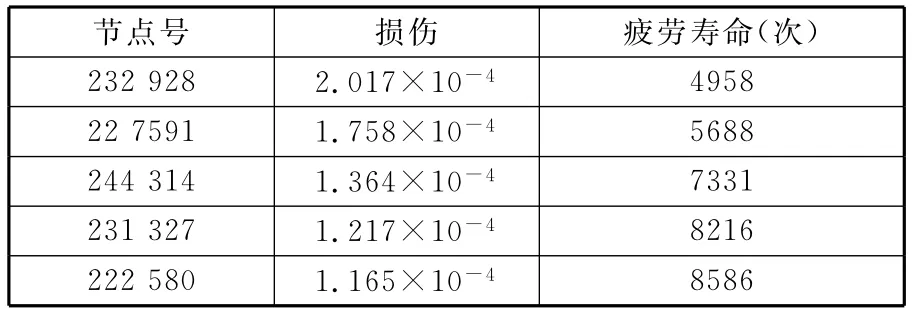
表2 車架最危險點的疲勞壽命計算結果

4 結論

（1）指出了建立用于模態應力恢復的柔性體的關鍵步驟；采用模態應力恢復方法的疲勞計算，比以往的靜態、準靜態疲勞計算能更好地獲取零部件載荷歷程。

（2）在ADAMS中建立了整車剛柔多體模型，采用ADAMS／Car Ride，可以利用現實道路試驗數據（如試驗場路面激勵）作為對汽車的激勵，使路面激勵更具真實性，仿真結果可以與試驗場試驗及室內道路模擬試驗進行對比。

（3）在MSC公司提供的系列軟件環境下，集成地完成車架的疲勞測試，最大限度地減少了由于軟件兼容問題帶來的試驗誤差，有利于快速地評價車架等零部件的疲勞壽命。

（4）采用模態應力恢復方法得到車架的載荷應力，不同于以往的疲勞分析，即不需施加約束條件，排除了該環節產生的誤差對疲勞分析結果的影響。

（5）模態應力恢復的疲勞分析結果與試驗場道路試驗結果在失效位置和疲勞壽命方面有較好的一致性。

［1］ 劉獻棟，曾小芳，單穎春．基于試驗場實測應變的車輛下擺臂疲勞壽命分析［J］．農業機械學報，2009，40（5）：34－38．

［2］ 蔣國平，周孔亢．旅行車獨特懸架系統的運動特性［J］．機械工程學報，2008，44（4）：217－220．

［3］ 叢楠．軍用工程機械虛擬疲勞試驗研究［D］．湖南：國防科技大學，2006．

［4］ MSC．Documentation［M］．California：MSC．Software，2005．

［5］ 孫宏祝，叢楠，尚建忠．基于模態應力恢復的汽車零部件虛擬疲勞試驗方法［J］．汽車工程，2007，29（4）：274－278．

［6］ 王國軍．疲勞分析實例指導教程［M］．北京：機械工業出版社，2009．

［7］ 章適．基于模態應力恢復的車架疲勞壽命計算［D］．安徽：合肥工業大學，2010．

［8］ 李邦國．Patran2006與Nastran2007有限元分析實例指導教程［M］．北京：機械工業出版社，2007．

［9］ 馬愛軍．Patran和Nastran有限元分析專業教程［M］．北京：清華大學出版社，2005．

［10］ Lee Y L，Pan J，Hathaway R，et al．Fatigue Testing and Analysis［M］．New York：Elsevier Inc．，2005．