空氣彈簧在機械振動臺中的應用

趙曉敏

(西安三潤環境設備科技有限責任公司，西安 710068)

空氣彈簧是在一密閉容器中存儲壓力空氣，利用空氣的可壓縮性實現彈簧作用。空氣彈簧通常由彈簧本體、附加氣室和高度控制閥三部分組成。根據結構，可分為囊式和膜式兩種。囊式空氣彈簧可根據需要設計成單曲、雙曲和三曲；膜式空氣彈簧則有約束膜式和自由膜式兩種。機械振動臺上使用的是約束膜式空氣彈簧，約束膜式空氣彈簧的優點是剛度小，并且特性曲線容易通過約束裙的形狀來控制，缺點是由于橡膠簧的工作狀況復雜而使耐久性差。

在機械振動臺單自由系統中，空氣彈簧的作用主要為系統的支撐，作為系統的剛度和固有頻率計算的重要環節和依據。所以，空氣彈簧在機械振動系統中的應用以支撐剛度為主，減振隔振為副。

空氣彈簧作隔振用時有以下優點：

（1）空氣彈簧的剛度隨載荷而變，因而在任何負載下自振頻率幾乎保持不變，使彈簧裝置具有幾乎不變的性能；

（2）空氣彈簧具備非線性特性，能有效控制振動位移幅值；

（3）通過高度控制閥，可使空氣彈簧的工作高度在任何載荷下保持一致，也可使彈簧在同一載荷下具有不同的高度，因此，有利于適應囊式和膜式多種結構上的要求；

（4）空氣彈簧的剛度可以根據需要，借助于改變氣室的容積進行選擇，而且可以選擇的很低；

（5）同一空氣彈簧，能同時承受軸向和徑向載荷，也能傳遞扭矩，而通過內壓力的調整，還可以得到不同的承載能力，因此能適應多種載荷的需要；

（6）空氣彈簧各個方向吸振效果好，吸收高頻振動和隔音的性能好；

（7）在空氣彈簧本體和附加空氣室之間設一節流孔，能起到阻尼作用，如果節流閥孔徑選擇適當，可不設減振器。

1 空氣彈簧受力分析

空氣彈簧在機械振動臺上使用時，其“約束膜式”受力模型如圖1。

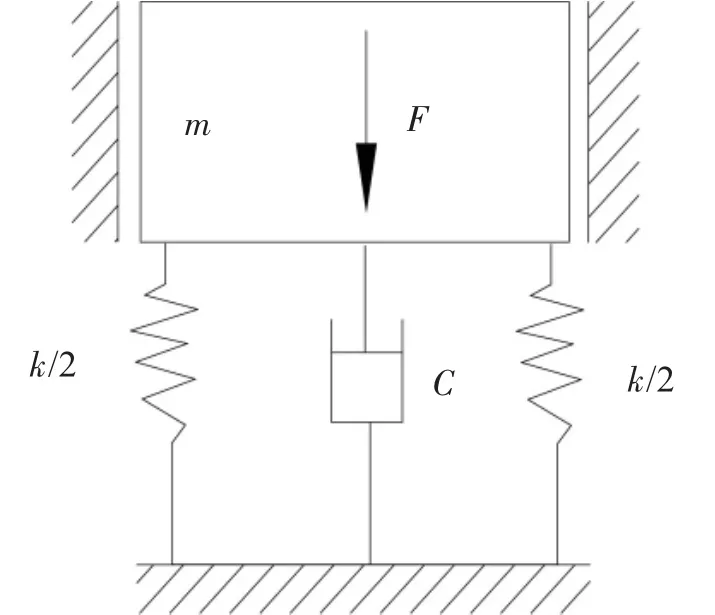
圖1 空氣彈簧在機械振動臺上使用時受力模型

此受力模型為單自由度受迫振動系統，當振動體受垂直方向激振力Fsinωt的作用時，位移為usin ωt，其運動方程為：

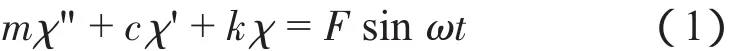
受迫振動的特解可表示為：

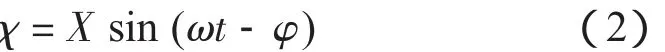
（1）、（2） 式中：m為質量，c為阻尼系數，k為剛度，X為振幅，χ為X的解，t為時間，Fsinωt為激振力，ω為激振頻率，φ為相位差。

其中，振幅：

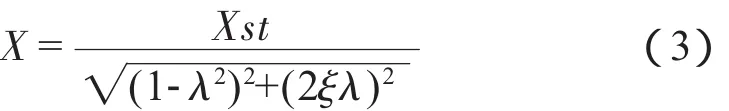
相位差為：

在以上的振幅和相位差計算公式中：

Xst=F/h——在與激振力幅值相等的靜力P作用下系統的靜位移

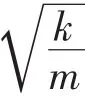
Cc=——臨界阻尼系數。

可得：

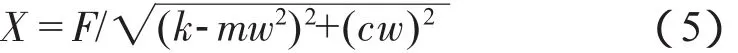
所以，傳至地面的力不是Fsinwt，而是彈簧力kx和阻尼力cx'的和：

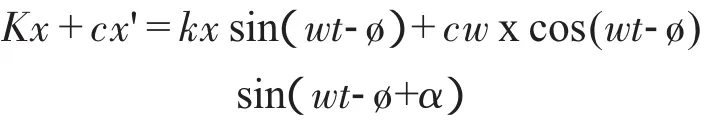
其幅值為：

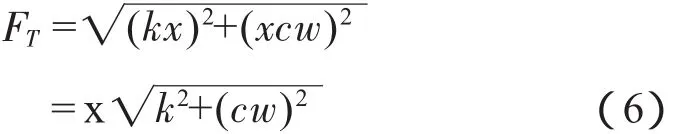
將式(5）帶入式(6），得:

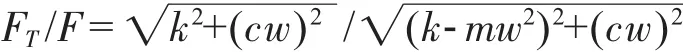
因為 ξ=c/2ωnm，γ =ω/ωn，所以

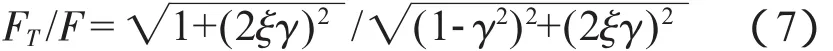
倘若阻尼忽略不計，則（式2-7）變化為：

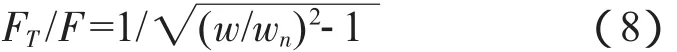
FT/F實際傳遞力的幅值與不平衡力的力值之比，稱為傳遞率。分析式(8）可知，要使振動臺的不平衡力不傳遞到底座，或者，要使底座的力不傳到振動臺，傳遞率FT/F要盡可能的小，即ω/ωn要盡可能大，也就是說ωn越小越好，即空氣彈簧的一階諧振頻率盡可能低。

2 空氣彈簧的設計

根據GB 2423.10《電工電子產品基本環境試驗規程試驗Fc：振動(正弦)試驗方法》，機械振動臺的工作下限頻率f1小于或等于5 Hz。一般取空氣彈簧一階諧振頻率f0≤（1/3-1/2）f1，空氣彈簧受力簡圖如圖2。

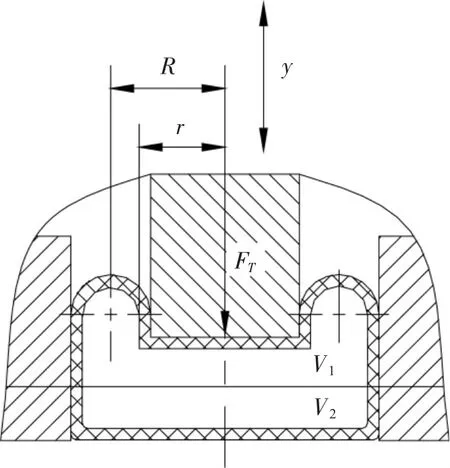
圖2 空氣彈簧受力時分析圖

假定，空氣彈簧變形前后，其橡膠囊經線（縱剖面）方向上斷面保持不變；斷面長度保持不變。

其中：

FT為空氣彈簧承受的力；

Y為振動臺振動時不平衡力作用引起空氣彈簧振動，其位移幅值為y；

V1為空氣彈簧標準狀態下內容積；

V2為附加氣室標準狀態下內容積。

在標準狀態下，根據靜力學平衡原理，有：

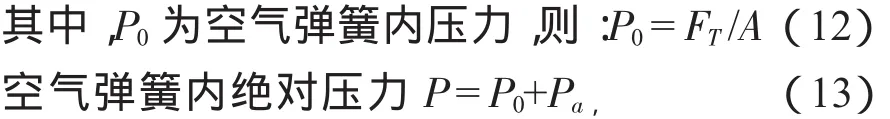
其中，Pa為大氣壓力，一般取1 kgf/cm2

當空氣彈簧以位移幅值y振動時，空氣彈簧內容積的變化量為：

當空氣彈簧向上振動時，內容積增大，壓力減小，其內容積變為：

其壓力變為：Pmin=P(V0/Vmax)m

其中，m為多變指數，1≤m≤1.4，在等溫過程中，m=1；在絕熱過程中，m=1.4。

當空氣彈簧向下振動時，內容積減小，壓力增大，其內容積變為：

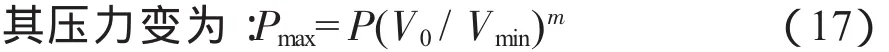
為使空氣彈簧具備理想的非線性，可調整附加氣室內容積V2，那么空氣彈簧的軸向剛度為：

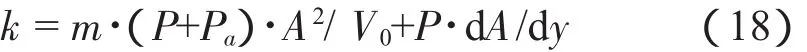
其中，dA/dy為有效承載面積變化率，根據前面受力分析時假定的條件，dA/dy=0，則空氣彈簧的軸向剛度為：

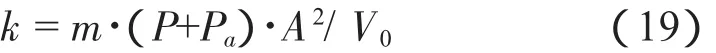
同理，空氣彈簧的徑向剛度為：

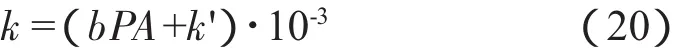
其中，b為空氣彈簧形狀系數，b=π/(4r)；

k'為簧囊本身徑向剛度；

A為空氣彈簧的有效承載面積。

式中，g為重力加速度，一般取981 cm/s2。

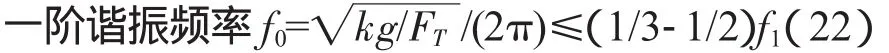
在機械振動臺上，4個空氣彈簧分別連接4個氣室，這4個氣室又串聯在一起，一階諧振頻率約5×(1/3)=1.78 Hz，所以機械臺的一階諧振頻率較低。

所以，空氣彈簧必須滿足條件：

3 幾個影響因素分析

氣室與附加氣室容積的比例，空氣彈簧形狀、材料、尺寸，以及氣室與附加氣室之間的節流孔的大小，對系統剛度和固有頻率都有一定的影響。

（1）附加氣室容積對系統剛度和一階諧振頻率的影響。由式（19）可看出，有效容積越大，軸向剛度越低。所以給空氣彈簧連一附加空氣室，可減少空氣彈簧的軸向剛度。

以空氣彈簧為彈性元件的空氣懸架系統表現出了諸多的優越性，如果在此基礎上再增加一附加氣室組成帶附加氣室空氣彈簧系統，還可以進一步提高懸架系統的減振性能。橡膠空氣彈簧與附加空氣室相連，可使橡膠空氣彈簧裝置的固有振動頻率降低到0.5～3 Hz。在任何載荷的作用下，橡膠空氣彈簧都可以保持較低而近乎相等的振動頻率。

研究結果表明，附加氣室容積為主氣室容積的2倍時，附加氣室與空氣彈簧間的節流孔由小變大過程中，可以使系統等效剛度降低60%左右，系統固有頻率降低0.5～3 Hz，系統等效阻尼比呈現先增大后減小的趨勢。附加氣室容積的增大使得系統等效剛度和固有頻率降低，但當附加氣室容積大于主氣室容積2～3倍后，附加氣室容積的增大對系統的等效剛度和固有頻率影響便不再明顯。

另外，改變附加氣室容積對系統的位移傳遞率、動載荷及響應加速度也具有顯著的影響，在附加氣室容積小于主氣室容積2倍的范圍之內時，附加氣室容積的增大能夠顯著降低系統在共振頻率點的位移傳遞率、加速度均方根值以及最大動載荷，但當附加氣室容積超過主氣室容積2倍時，附加氣室容積的增大對以上3個指標的影響不再明顯。

（2）簧囊橡膠材料本身剛度對系統一階諧振頻率的影響。試驗證明，橡膠氣囊材料本身剛度對空氣彈簧剛度影響極大，這是造成空氣彈簧剛度理論值與試驗值差異較大的原因。橡膠氣囊材料剛度越大，空氣彈簧的剛度就越大，其一階諧振頻率越高，其結果提高了系統工作時最小工作頻率。所以，橡膠氣囊隔震系統應當減小材料剛度，減小自振頻率，使得空氣彈簧隔振器的承載能力留有足夠的余量情況下，系統最小工作頻率盡可能低。

（3）振動臺橫向振動時，簧囊橡膠材料剛度要大得多。橡膠空氣彈簧的本體結構柔軟，因此具有軸向、橫向和旋轉向的綜合隔振作用。機械式振動臺橫向振動時，簧囊橡膠材料剛度要大得多。

（4）在空氣彈簧和附加氣室之間設一節流孔，當空氣流過節流孔時，由于阻力而吸收一部分振動能量，從而起到減振阻尼的作用。除了影響系統的剛度和固有頻率之外，節流孔的大小主要影響了系統的阻尼。

試驗證明，系統剛度隨節流孔開度增大而減小，阻尼隨節流孔的增大先增大后減小，附加氣室容積的增大能使系統剛度減小并使阻尼比增大，激勵頻率的增大會增大系統剛度并減小系統阻尼比，靜載荷的變化對系統振動特性影響不大。

4 結束語

本文所述是一個針對機械振動臺單自由系統中空氣彈簧作為支撐時和減振隔振時系統的剛度和固有頻率計算，實用性很強。

需要指出的是：文中的原理示意圖及結構示意圖是實際系統的簡化，旨在說明原理，而并非是實際系統的復現。

[1]季文美，方同，陳松淇.機械振動[M].北京：科學出版社.1985.51-59.

[2]陳英會.彈簧[M].北京：機械工業出版社.1986.36-57.

[3]機械設計手冊編委會.第二卷/機械設計手冊（第3版）[M].北京：機械工業出版社.2004.