四邊固支功能梯度板中波的傳播

孫 丹，羅松南

(湖南大學 力學與航空航天學院，長沙 410082)

功能梯度材料(FGM)是一種近期發展的新型材料，它一般由兩種性質不同的材料介質沿空間按不同組分復合而成，形成材料性質和功能沿厚度呈梯度變化，從而滿足材料構件不同部位對材料不同性質的要求。同時，由于功能梯度材料組成和結構在空間上呈連續變化，不存在明顯的界面和性能突變，因此具有明顯優于一般復合材料的特性［1－3］。它的出現對于推動材料科學的發展具有重大的意義。

梯度功能材料中波的傳播性質的研究已備受國內外學者的關注，張立剛等［4－5］研究了梯度功能材料中SH波的傳播問題，利用WKBJ理論求出了梯度功能材料位移的近似解，還對均勻覆層梯度功能半空間中的Love波頻散問題進行了研究;劉睫［6］和王子昆［7］研究了梯度材料層狀結構中的Love波和梯度介質半空間Rayleigh面波的傳播性能;Li［8］利用彈性波理論和WKB方法研究了壓電功能梯度層中Love波傳播的問題;Han［9］應用分層理論研究了SH波在功能梯度板中傳播的問題，分析了功能梯度材料對SH波傳播的影響;Arkadi Berezovski［10］討論了二維應力波在功能梯度層中的傳播;Chen［11］研究了功能梯度板中彎曲波的彌散問題;Chakraborty［12］應用有限元對功能梯度梁中波的傳播問題進行了研究。

本文研究了波在四邊固支各向同性功能梯度板中傳播的問題。考慮剪切變形和轉動慣性的影響，采用一階剪切變形板理論和小應變的應變－位移關系，利用Hamilton原理建立了動力學基本方程式，應用伽遼金法消除偏微方程式的空間變量，由運動控制方程推得頻散方程。分別給出了頻率﹑相速度和群速度隨波數變化的曲線，分析了材料的功能梯度指數對頻率﹑相速度和群速度的影響規律。

1 動力學基本方程式

考慮彈性波在如圖1所示的各向同性功能梯度板中傳播。計及剪切變形和轉動慣性的影響，采用一階剪切變形板理論和小應變的應變－位移關系。

圖1 功能梯度板模型Fig.1 The model of the FGM plate

根據一階剪切變形板理論，位移場分量假設為:

式中u0，v0，w0是板的中面位移，φx和 φy分別為中面法線在x方向與y方向的轉角。

依據小應變的應變－位移關系，應變分量為:

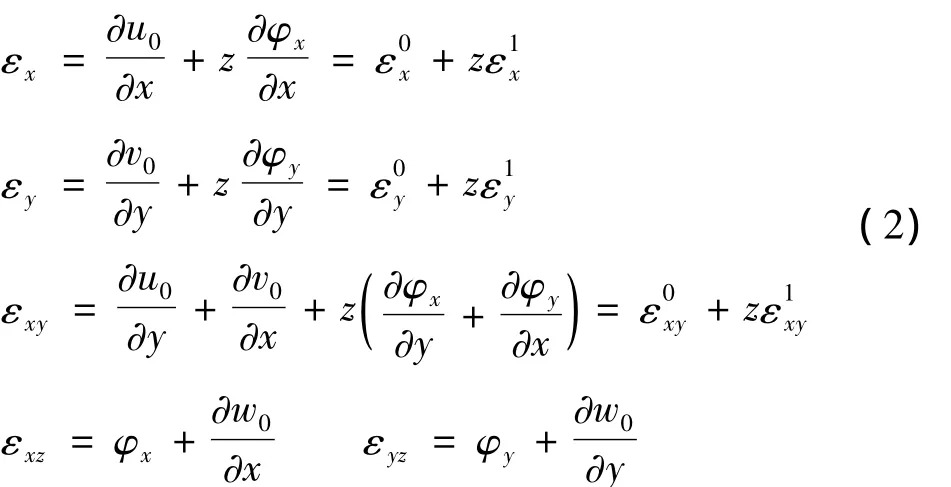
材料的應力－應變關系可表示為:

其中:

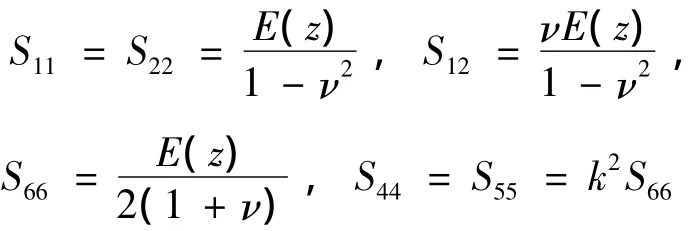
k2是剪切修正因子。

功能梯度板的內力與應力關系為:

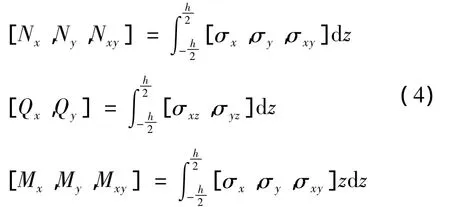
其中 Nx，Ny，Nxy是膜力，Qx，Qy是橫向剪力，Mx，My，Mxy是彎矩和扭矩。

將式(3)代入式(4)中，并應用式(2)，得功能梯度板的本構關系:

以及

式中

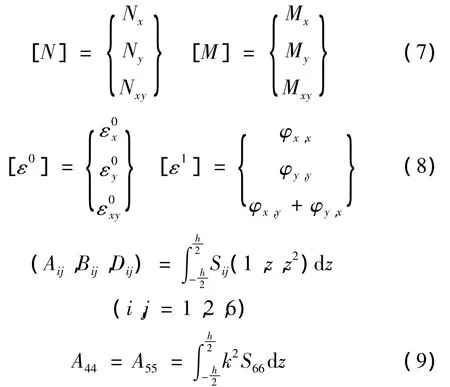
這里Aij，Bij和Dij分別是功能梯度板的薄膜剛度﹑耦合剛度和彎曲剛度。

在忽略體力和不存在面力的情況下，利用Hamilton原理可推得運動控制方程

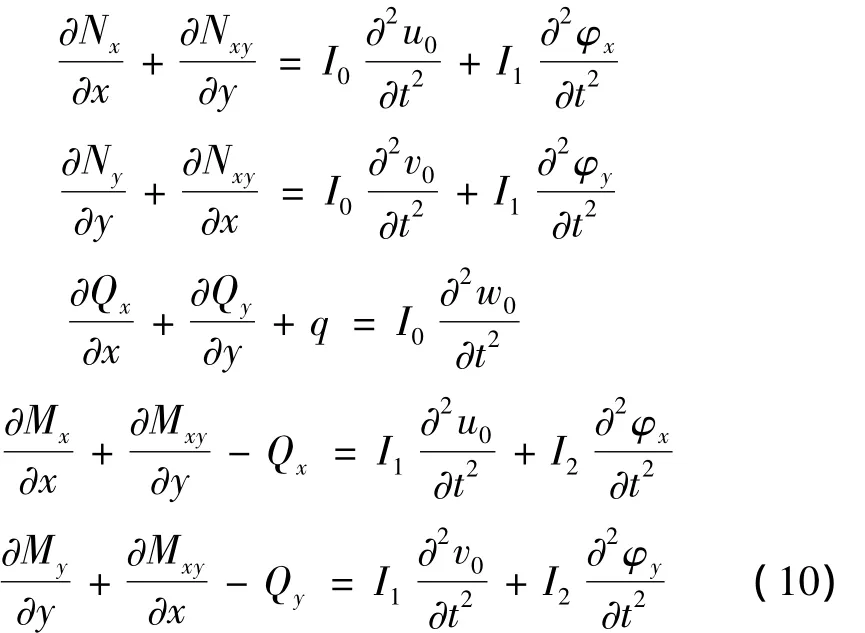
其中:

應用本構關系(5)，運動控制方程(10)可進一步推得為:

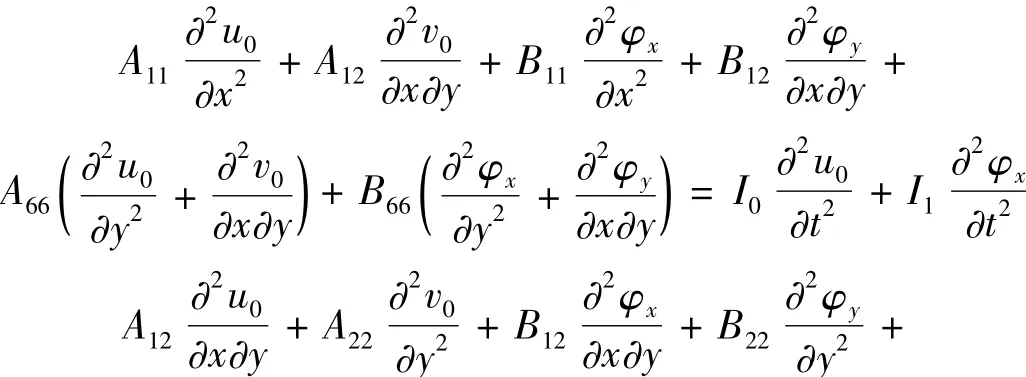
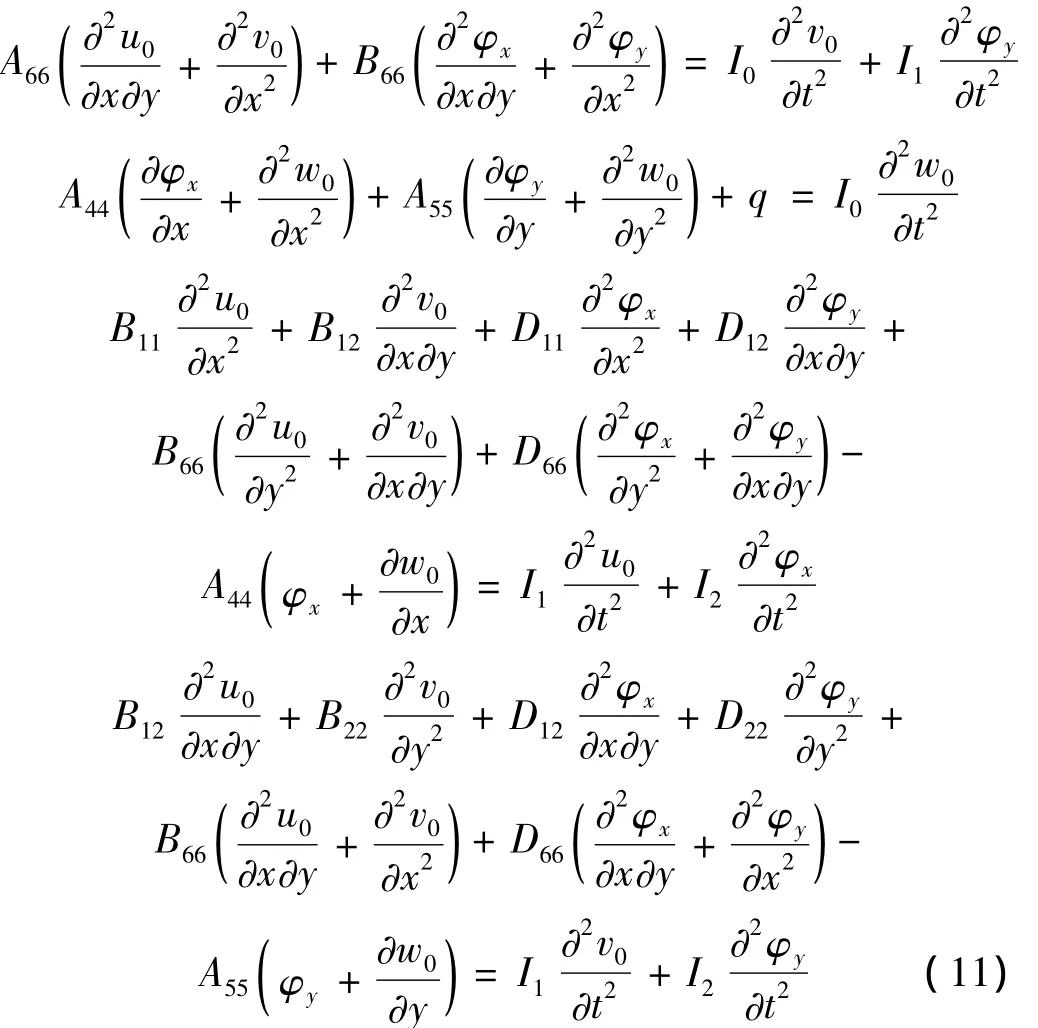
四邊固支板的邊界條件為:

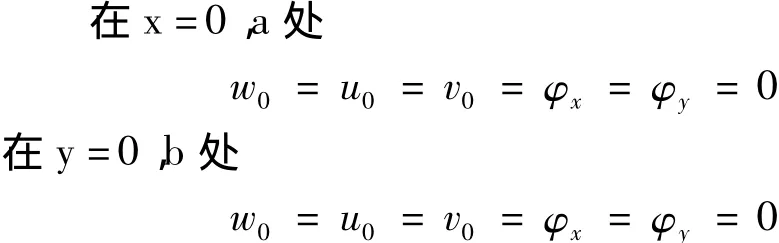
2 頻散方程

當彈性波在功能梯度板中傳播時，為尋求方程組式(11)滿足邊界條件的解，取位移形函數為:

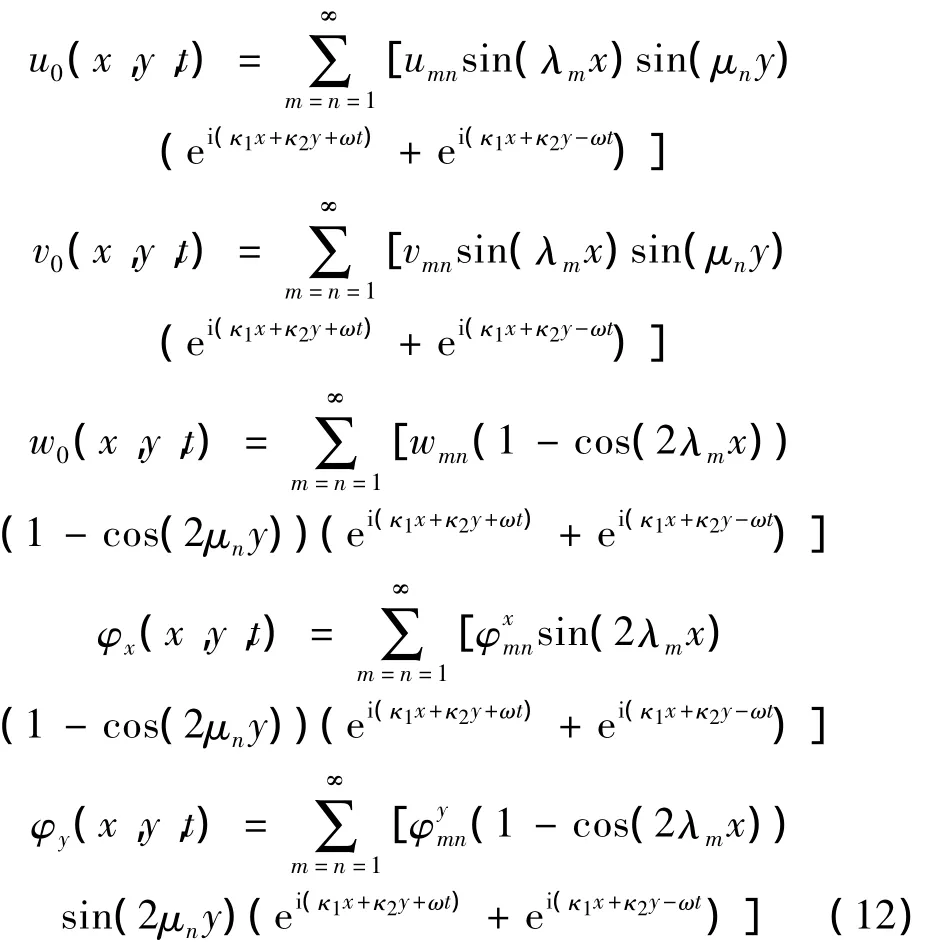
其中，umn，vmn，wmn，分別 為波幅系數，sin(λmx)，sin(μny)，sin(2λmx)，sin(2μny)，cos(2λmx)和，分別為梁的振形函數，和μ=n，κ和κ分別為波數 κ在x軸向和y軸向的分量，12ω為諧波頻率。

把位移型函數(12)式代入運動控制方程組(11)，對結果方程組的第一﹑二式分別乘以 sin(λrx)·sin(μjy)，第三式乘以(1 － cos(2λrx))(1 － cos(2μiy))，第四式乘以 sin(2λrx)(1 －cos(2μiy)，第五式乘以(1－cos(2λrx))sin(2μjy)，然后分別對坐標x從0到α積分和對坐標y從0到b積分，且利用梁振形函數的正交性條件，可將運動控制方程組(11)表示為:

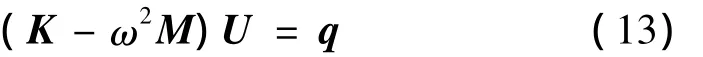
令板所受外荷載為零，且取m=n=1，可得:

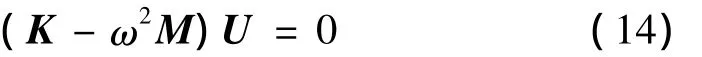
其中:

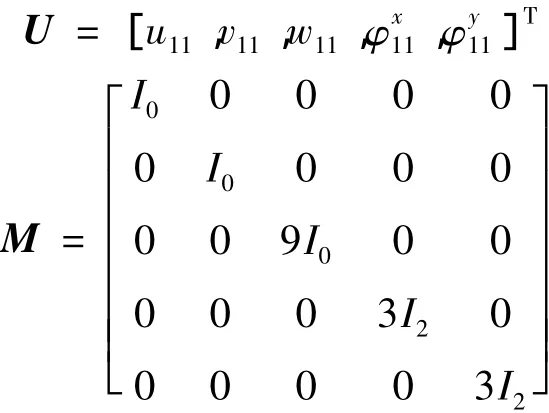
K為5×5矩陣，其元素均為與波數相關已知常數。

要使U有非零解，則必有:

式(15)就為頻散方程。

κ1和 κ2可用波數 κ 表示為:κ1=κcosφ，κ2=κsinφ，，考慮到材料在x，y方向具有同性性質，設。相速度，群速度從頻散方程(15)可求得五對解，它們分別對應五種模態，這五種模態分別為 T0，T1，T2，T3和 T4，其中 T0，T3和T4對應于彎曲波，T1和T2對應于膨脹波。

3 數值計算和分析

功能梯度板中功能梯度材料的參數可表示為:

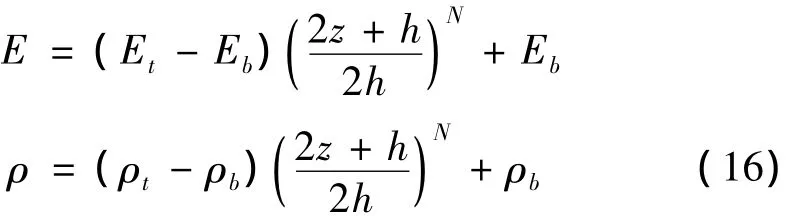
其中，N(N＞0)為功能梯度指數，N=0時為均質材料;Et，Eb，ρt，ρb為板的頂部和底部的彈性模量和質量密度。

取 a=0.2 m，b=0.2 m，h=0.02 m;彈性模量Et=151 GPa，Eb=70 GPa，密度 ρt=3000kg/m，ρb=2707kg/m;泊松比 νt=0.3，νb=0.3 的梯度功能板進行計算和分析。

圖2和圖3給出了均質板(N=0)和不同功能梯度指數(N=1，2)的功能梯度板的頻散曲線。從圖2中可以看到在波數κ相同時，波在均質板(N=0)中傳播的頻率明顯的大于波在N=1的功能梯度板中傳播的頻率;在圖3中也可以看到，在波數 κ相同時，波在N=1的功能梯度板中傳播的頻率也大于波在N=2的功能梯度板中傳播的頻率。可見，當波數κ相同時隨著功能梯度指數N的增加，波在板中傳播的頻率隨著減小，而波在均質板(N=0)中傳播的頻率最大。

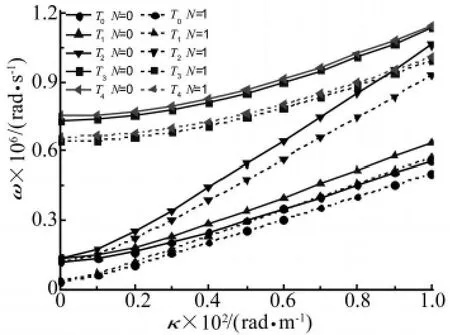
圖2 N=0和N=1時的頻散曲線Fig.2 The dispersion curves of FGM plate when N=0 and N=1

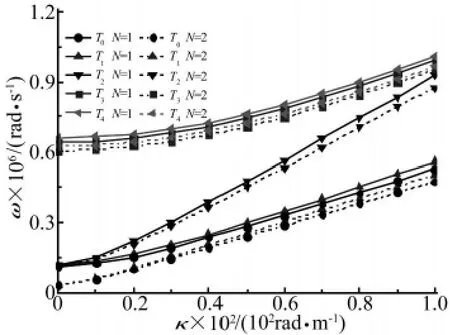
圖3 N=1和N=2時的頻散曲線Fig.3 The dispersion curves of FGM plate when N=1 and N=2

相速度C隨波數κ變化的曲線如圖4和圖5所示。從中同樣可以看到，當波數κ相同時，波在均質板(N=0)中傳播的相速度相對最大，波在N=1的功能梯度板中傳播的相速度次之，波在N=2的功能梯度板中傳播的相速度相對最小。

由上可知，當波數κ相同時隨著功能梯度指數N的增加，波在板中傳播的相速度隨著減小，而波在均質板(N=0)中傳播的相速度最大。

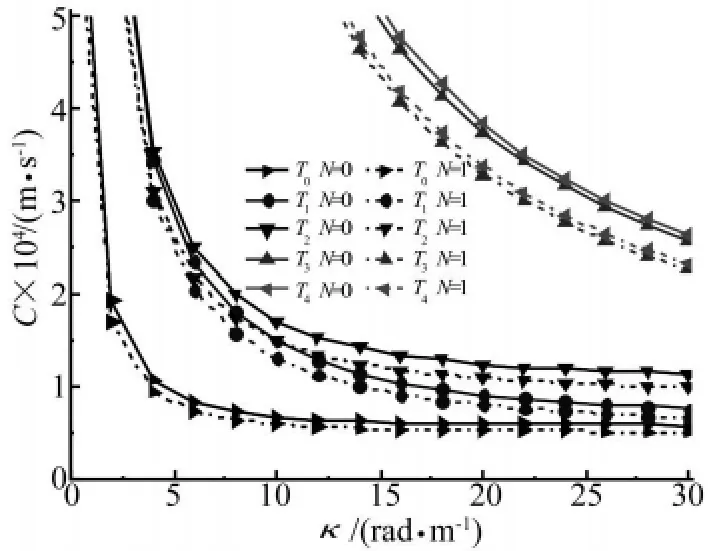
圖4 N=0和N=1時的相速度C隨波數κ變化曲線Fig.4 The phase velocity curves of FGM plate when N=0 and N=1

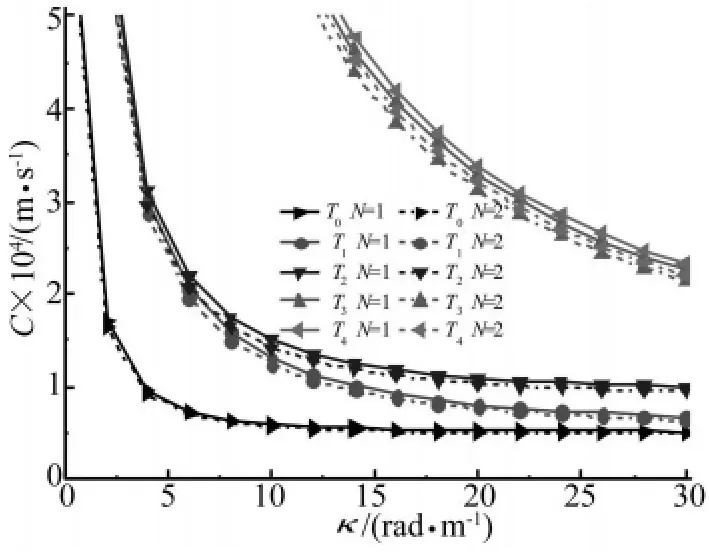
圖5 N=1和N=2時的相速度C隨波數κ變化曲線Fig.5 The phase velocity curves of FGM plate when N=1 and N=2

群速度Cg隨波數κ變化的曲線如圖6和圖7所示，從圖中可以看到當波數κ相同時，波在均質板(N=0)中傳播的群速度最大，在N=1的功能梯度板中傳播的群速度次之，在N=2的功能梯度板中傳播的群速度最小。由此可見，當波數κ相同時，同樣的隨著功能梯度指數N的增加，波在板中傳播的群速度也隨著減小，而波在均質板(N=0)中傳播的群速度最大，功能梯度材料的非均勻性對波的傳播具有阻礙作用。

圖6 N=0和N=1時的群速度Cg隨波數κ變化曲線Fig.6 The group velocity curves of FGM plate when N=0 and N=1

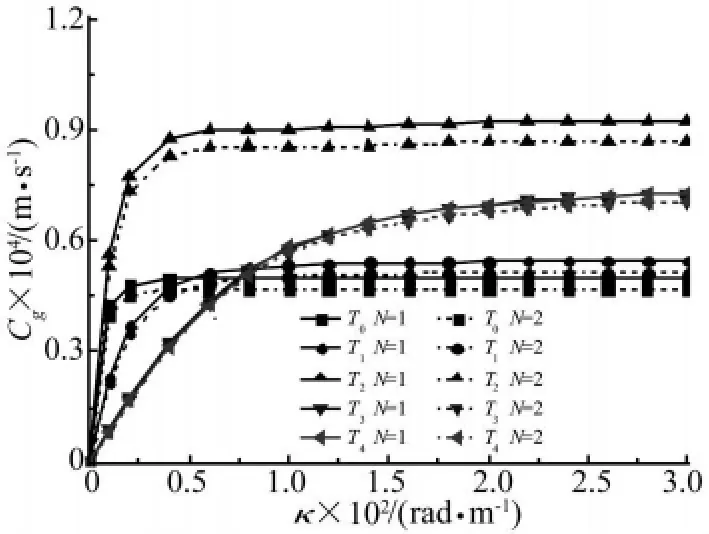
圖7 N=1和N=2時的群速度Cg隨波數κ變化曲線Fig.7 The group velocity curves of FGM plate when N=1 and N=2

4 結論

本文考慮剪切變形和轉動慣性的影響，采用一階剪切變形板理論，利用Hamilton原理推得運動控制方程，并應用伽遼金法消除空間變量，利用特征方程式得到了頻散方程。分別給出了頻率﹑相速度和群速度隨波數變化的曲線。分析了隨著材料性質指數(功能梯度指數)的變化，材料性質對波傳播的影響規律:當波數相同時，隨著功能梯度指數的增大，波在梯度板中傳播的頻率﹑相速度和群速度都隨著減小，且波在均質板中(N=0)傳播的頻率﹑相速度和群速度最大。可見，功能梯度材料的非均勻性對波的傳播具有阻礙作用，且隨著功能梯度指數的增大阻礙性越強。這些結論都為制備和使用功能梯度材料提供了理論依據。

［1］Koizumi M.The concept of FGM［J］.Geramic Trans，Functionally Gradient Materials，1993，34:3－10.

［2］Hirai T，Chen L.Recent and prospective development of functionally graded materials in Japan［J］.Mater Sci Forum，1999，308－311:509－514.

［3］張宇民，赫曉東，韓英才.梯度功能材料［J］.宇航材料工藝，1998，5:5－10.

［4］張立剛，蓋秉政，朱 虹.梯度功能材料中SH波的傳播［J］.哈爾濱商業大學學報，2007，23(1):80－83.

［5］張立剛，蓋秉政，朱 虹.均勻覆層梯度半空間中的Love面波［J］.西安交通大學學報，2007，41(3):372－376.

［6］劉 睫，王子昆，張 陵.梯度材料層狀結構中的Love波［J］.固體力學學報.2004，25(2):165－170.

［7］劉 睫，王子昆.梯度介質半空間Rayleigh面波傳播性能研究［J］.應用力學學報，2004，21(3):106－109.

［8］Li X Y，Wang Z K，Huang S H.Love wave in functionally graded piezoelectric material［J］.International Journal of solids and Structures，2004，41:7309 －7328.

［9］Han X，Liu G R.Effects of SH waves in a functionally graded plate［J］.Mechanics Research Communications，2002，29:327－338.

［10］Berezovski A，Engelbrecht J，Maugin G A.Numerical simulation of Two-dimensional wave propagation in functionally graded materials［J］.European Journal of Mechanics A/Solids，2003，22:257 －265.

［11］Chen W Q，Wang H M，Bao R H.On calculating dispersion curves of waves in a functionally graded elastic plate［J］.Composite Structures，2007，81:233－242.

［12］Chakraborty A，Gopalakrishnan S.A spectrally formulated finite element for wave propagation analysis in functionally graded beas［J］.International Journal of solids and Structures，2003，40:2421－2448.