帶網(wǎng)狀筋壁板彎曲中性層近似計(jì)算方法

邊洪錄，趙長(zhǎng)喜，賴(lài)小明

（北京衛(wèi)星制造廠(chǎng)，北京 100190）

0 引言

隨著我國(guó)載人航天事業(yè)的發(fā)展，長(zhǎng)期有人居住的空間站計(jì)劃已經(jīng)被列入日程。空間站主結(jié)構(gòu)為大型密封艙結(jié)構(gòu)，由整體壁板焊接而成。根據(jù)北京衛(wèi)星制造廠(chǎng)現(xiàn)有壁板的制造流程，彎曲后的壁板外形不再進(jìn)行機(jī)械加工，因此對(duì)于壁板的彎曲展開(kāi)尺寸精度要求較高。確定壁板彎曲后展開(kāi)中性層與彎曲內(nèi)表面的距離（簡(jiǎn)稱(chēng)中性層位置）成為壁板制造過(guò)程中的關(guān)鍵步驟。

本文分析了整體壁板的結(jié)構(gòu)特點(diǎn)，介紹了中性層位置計(jì)算的簡(jiǎn)化原則，通過(guò)計(jì)算確定了整體壁板中性層的位置，并與彎曲試驗(yàn)實(shí)測(cè)結(jié)果進(jìn)行了比對(duì)，證明了該計(jì)算方法的有效性。這為今后結(jié)構(gòu)近似的壁板展開(kāi)計(jì)算提供了可靠的依據(jù)。

1 壁板的結(jié)構(gòu)特點(diǎn)

整體壁板采用鋁合金材料，材料牌號(hào)為5A06，其性能見(jiàn)表1。網(wǎng)格的長(zhǎng)度和寬度均在150 mm左右。壁板彎曲后的內(nèi)半徑在500～3 000 mm之間；單塊壁板的最大展開(kāi)長(zhǎng)度小于3 000 mm，其尺寸精度要求為±0.5 mm。

2 板材彎曲理論及假設(shè)

2.1 板材彎曲理論

板材在外界力矩的作用下，其變形區(qū)（圖1中的ABCD區(qū)域）的曲率發(fā)生變化。在整個(gè)彎曲過(guò)程中，板材變形區(qū)外表面拉伸，內(nèi)表面壓縮。隨著力矩的增大，板材彎曲程度逐漸增大，內(nèi)部應(yīng)力-應(yīng)變變化可分為3個(gè)階段：純彈性彎曲階段，彈塑性彎曲階段，純塑性階段。各階段板材變形區(qū)內(nèi)部切向應(yīng)力分布如圖1中的(a)、(b)、(c)所示[1]。

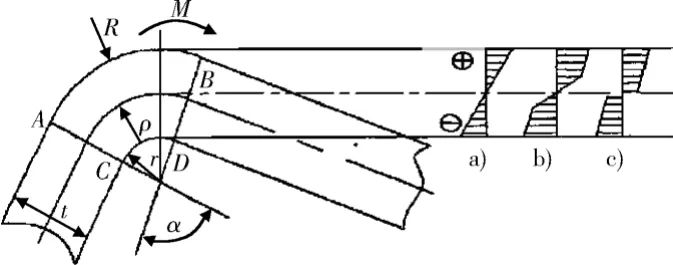
圖1 彎曲時(shí)板材變形區(qū)內(nèi)部切向應(yīng)力分布圖Fig.1 Internal tangential stress distribution of curly plate material in deformation region

根據(jù)壁板結(jié)構(gòu)特點(diǎn)可知，整體壁板彎曲變形區(qū)多處于彈塑性彎曲階段。

2.2 壁板彎曲假設(shè)

由于板材彎曲過(guò)程中塑性形變方程較為復(fù)雜，

表 1 壁板材料性能表Table 1 Material properties of thin-walled plate

壁板為方形網(wǎng)格結(jié)構(gòu)，主要包括腹板和加強(qiáng)筋兩部分。腹板厚度為2.5～3mm；加強(qiáng)筋寬度為4～5 mm，高度約為17～17.5mm，壁板總厚度為20 mm。為了簡(jiǎn)化中性層位置的計(jì)算，在滿(mǎn)足運(yùn)算精度的同時(shí)，作出下述的假設(shè)：

1）假設(shè)壁板所采用的材料為理想塑性材料；

2）假設(shè)塑性彎曲時(shí)，壁板仍滿(mǎn)足平面假設(shè)；

3）假設(shè)變形區(qū)內(nèi)部彈性變形仍滿(mǎn)足彈性彎曲理論；

4）假設(shè)壁板彎曲過(guò)程中應(yīng)力中性層和應(yīng)變中性層重合。

同時(shí)根據(jù)壁板的結(jié)構(gòu)特點(diǎn)，對(duì)壁板沿彎曲線(xiàn)的剖面進(jìn)行簡(jiǎn)化。由于壁板沿彎曲線(xiàn)的剖面實(shí)際上由數(shù)個(gè)變化的T型截面組成，因此根據(jù)對(duì)稱(chēng)原則，可將壁板沿彎曲線(xiàn)方向的剖面簡(jiǎn)化為單個(gè)T型截面。簡(jiǎn)化后的T型截面與原壁板T型截面的幾何形心位置相同，其形狀如圖2所示。

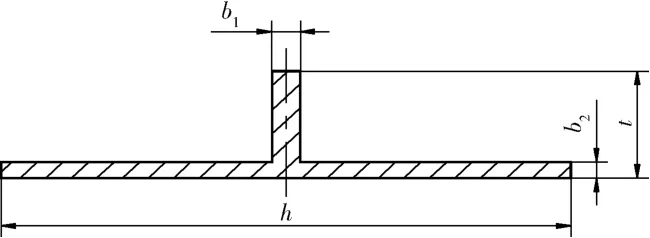
圖2 簡(jiǎn)化后的T型截面Fig.2 Reduced cross-section profile

3 中性層位置的計(jì)算方程建立

中性層位置的計(jì)算是建立在上述假設(shè)的基礎(chǔ)上，即沿彎曲線(xiàn)方向的T型剖面形狀不發(fā)生變化，其位置僅隨彎曲角的變化而變化，且剖面上的總合力為零。

假設(shè)壁板彎曲半徑為R，拉伸區(qū)域的合力為Ft，其面積為At；壓縮區(qū)域的合力為Fc，其面積為Ac。根據(jù)本文第2節(jié)中的假設(shè)2），有：

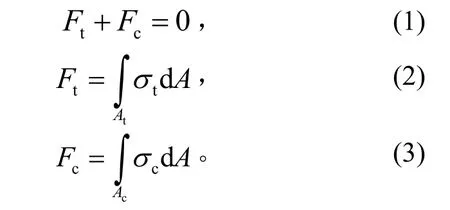
將式(2)與式(3)代入式(1)，可得：

根據(jù)板材彎曲理論，假設(shè)壁板彎曲后的中性層半徑為ρ，變形區(qū)內(nèi)距中性層y處纖維的切向應(yīng)變?yōu)閇2]：

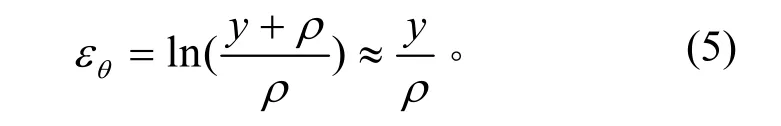
由式(5)可知，壁板變形區(qū)內(nèi)的切向應(yīng)變?chǔ)圈排c距中性層的距離y近似成正比例關(guān)系。在中性層附近以彈性變形為主。若已知彈性變形階段最大切向應(yīng)變sε，則根據(jù)相似三角形關(guān)系，可確定壁板變形區(qū)內(nèi)部彈性變形部分的厚度

式中sε為壁板彈性變形階段產(chǎn)生的最大切向應(yīng)變。結(jié)合上述分析結(jié)果及T型截面的幾何特性，可知此時(shí)壁板變形區(qū)內(nèi)的剖面上切向應(yīng)力分布，如圖3所示。

圖3 壁板變形區(qū)沿彎曲線(xiàn)方向剖界面切向應(yīng)力分布圖Fig.3 Tangential stress distribution of cross section along curved line direction in plate deformation region

圖中：yc為壁板中性層距彎曲內(nèi)表面的距離；t為壁板厚度；σt、σc為壁板材料拉伸和壓縮時(shí)屈服強(qiáng)度。

根據(jù)彎曲變形區(qū)內(nèi)的幾何關(guān)系，中性層彎曲半徑可表示為：

由圖3及假設(shè)1）可知，當(dāng)壁板拉伸區(qū)域的最外側(cè)和壓縮區(qū)域的最內(nèi)側(cè)均處于塑性變形區(qū)域時(shí)，則有

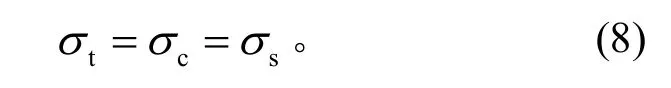
根據(jù)圖3中的幾何關(guān)系，當(dāng)壁板中性層兩側(cè)的拉伸和壓縮區(qū)域處于彈性變形區(qū)域時(shí)，距中性層x處的應(yīng)力為：

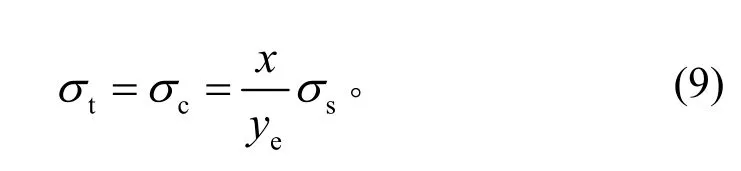
將式(5)～(9)帶入式(4)，就可得到關(guān)于壁板中性層位置的計(jì)算方程。

4 中性層位置與彎曲半徑的關(guān)系

本文采用MatLab軟件進(jìn)行編程求解中性層位置方程。求解思路如下：

1）根據(jù)截面形心位置和完全塑性彎曲狀態(tài)下的中性層位置確定中性層位置的變化區(qū)間。

2）使用二分法假設(shè)中性層位置，并計(jì)算此位置下的切向合力。

3）判斷合力是否為零。如果合力為零，則此位置為該狀態(tài)下的中性層位置。

4）如果合力不為零，則利用二分法重新確定中性層位置，對(duì)上述計(jì)算過(guò)程進(jìn)行迭代，直至找到切向合力為零。求解流程如圖4所示。

根據(jù)中性層位置計(jì)算方程，對(duì)于截面形心位置距內(nèi)彎曲表面的距離為 3.7 mm的壁板，通過(guò)MatLab軟件求解并描繪出壁板中性層位置和彎曲半徑的關(guān)系，如圖5所示。

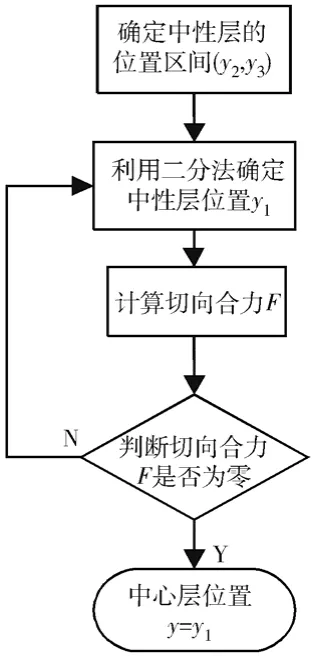
圖4 中性層位置求解流程圖Fig.4 Flow chart for solution of neutral layer

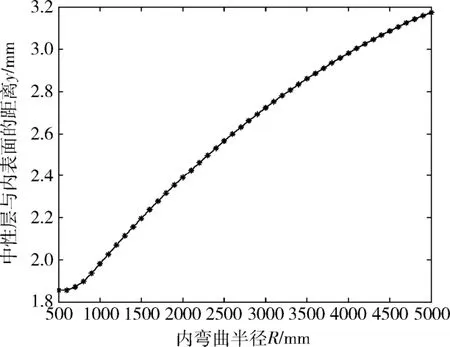
圖5 中性層位置與彎曲半徑的關(guān)系圖Fig.5 Relationship between neutral layer position and bending radius

由中性層位置計(jì)算方程及圖5可知：壁板彎曲過(guò)程處于彈塑性階段時(shí)，中性層位置曲線(xiàn)為拋物線(xiàn)；當(dāng)內(nèi)彎曲半徑R＜ 600 mm時(shí)，中性層位置基本不再發(fā)生變化，因此可以近似認(rèn)為此時(shí)壁板彎曲已進(jìn)入純塑性階段。

5 實(shí)測(cè)數(shù)據(jù)與理論計(jì)算結(jié)果的對(duì)比分析

壁板彎曲中性層位置的彎曲試驗(yàn)測(cè)量數(shù)據(jù)與計(jì)算結(jié)果列于表2。

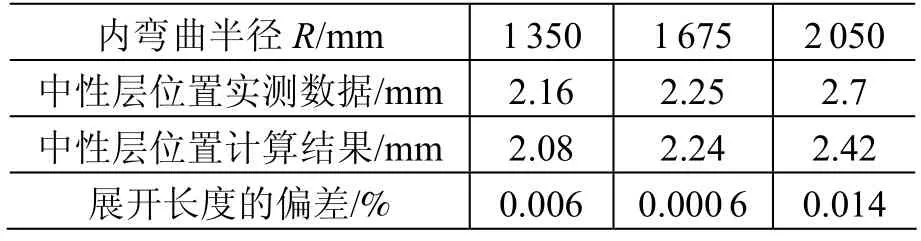
表2 中性層位置實(shí)測(cè)數(shù)據(jù)與計(jì)算結(jié)果對(duì)比Table 2 Comparison between measured data and computed result of the neutral layer’s location

式中：L實(shí)為實(shí)際展開(kāi)長(zhǎng)度；L理為理論計(jì)算展開(kāi)長(zhǎng)度；y實(shí)為實(shí)測(cè)的中性層位置；y理為理論計(jì)算的中性層位置；R為壁板的內(nèi)彎曲半徑。

由于材料、加工工藝和加工設(shè)備的限制，單塊壁板的展開(kāi)長(zhǎng)度小于3 000 mm，因此展開(kāi)長(zhǎng)度誤差小于0.42 mm，能夠滿(mǎn)足壁板展開(kāi)的精度要求。

6 結(jié)論

本文通過(guò)對(duì)壁板彎曲過(guò)程的分析及中性層位置計(jì)算方程求解結(jié)果和彎曲試驗(yàn)實(shí)測(cè)結(jié)果對(duì)比分析，得到如下結(jié)論：1）壁板彎曲過(guò)程處于彈塑性階段時(shí)，中性層位置曲線(xiàn)為拋物線(xiàn)；2）壁板彎曲中性層位置計(jì)算方程的計(jì)算結(jié)果能夠滿(mǎn)足現(xiàn)有產(chǎn)品壁板展開(kāi)長(zhǎng)度的精度要求；3）由于中性層位置方程的建立前提包含諸多假設(shè)，因此該方程的計(jì)算結(jié)果只是實(shí)際中性層位置的近似值。

（References）

[1]黃慶寶.板料成形及模具數(shù)值模擬分析[D].哈爾濱理工大學(xué)碩士學(xué)位論文, 2007

[2]胡世光.板材冷壓成形原理[M].北京： 國(guó)防工業(yè)出版社, 1979