基于正多面體法的單相異步電機優化設計
馬吉祥 孫 華
(1.上海交通大學電子信息與電氣工程學院,上海 200129;2.江蘇省吳江市供電公司,江蘇 吳江 215200)
單相異步電動機又稱單相感應電動機,具有結構簡單,價格低廉,運行可靠,維護使用方便等一系列優點,被廣泛運用于輕工設備,日用機電器具等諸多方面,成為最貼近人們生活的電機品種。隨著電力電子和控制技術的不斷發展,單相異步電機的控制性能也得到了很大的提升,因此對其進行優化設計,降低其成本,提高其性能是必然的趨勢。
傳統電機優化設計[1-2]采用的優化算法是一種基于設計變量可微分性的數值方法,主要有直接搜索法和隨機搜索法兩種尋優模式,其中經典尋優策略有Powell法、單純形法、懲罰函數法(SUMT)[3]、可變容差法和梯度法等等。20世紀90年代以來,模擬退火(SA)[4-8]、遺傳算法(GA)[9-14]、禁忌搜索(TS)[15]和模擬進化(SE)等現代啟發式優化算法得到迅速發展。其中懲罰函數法(SUMT)的懲罰因子常常難以選取;懲罰因子過大,函數會因對分配的權重過小而忽略對目標函數的影響,將給計算增加困難,懲罰因子過小,懲罰項得不到足夠的懲罰,滿足約束條件的精度就會降低。模擬退火算法(SA)的溫度控制難以掌握,計算量很大,需要太長的計算時間,直接影響了此算法的尋優能力。遺傳算法(GA)需要進行大量的目標特性的分析,如果目標分析方法比較耗時,計算量很大,此外在遺傳操作中會產生大量的不可行解,對參數的控制要求也比較嚴格,且易發生早熟現象。
正多面體法是一種約束優化的有效方法,收斂迅速,在搜索過程中只需要計算目標函數值,程序簡單,控制量少。算法包含平移、翻轉、收縮3個主要動作,利用搜索點的局部測試信息來尋找目標函數的下降方向,并向這個方向平移,越限后翻轉或者收縮,然后重復這樣的動作直至到達最優點。正多面體法適合于單相異步機這樣低成本,結構簡單的電機設計,是本文研究的算法。
1 正多面體算法的基本原理
1)選擇一個可行點(內點)X(0)作為初始點,在n維歐氏空間中生成一個以 X(0)為形心,邊長為T0的初始正多面體。此正多面體具有n+1個頂點。
2)在比較形心點 X(0)和正多面體n+1個頂點的目標函數數值以及約束滿足的情況下,使正多面體在n維空間執行平移,翻轉和收縮等3種基本搜索策略,并形成一個新的正多面體。在每次變動中必須滿足以下條件:
(1)在搜索過程中,始終保持形心在可行域D內。
(2)在搜索過程中,正多面體不發生畸變,始終保持為正多面體的形狀,只是位置或大小有所變化。
(3)每次搜索變動后,正多面體形心的目標函數值必須小于變動前的形心函數值。
反復運用上述3種基本搜索策略,使新的正多面體的形心 X(0)逐漸逼近最優點X*。
3)以2維的正三角形為例加以說明。
(1)平移:每在一個新的正多面體形成后,經過形心函數值和各頂點函數值比較后,如果有一個函數值最小的可行頂點 X(L),其函數值 FL比形心X(0)的函數值F0還要小時,正多面體就沿 X(0)X(L)連線方向平移搜索(如圖1所示)。
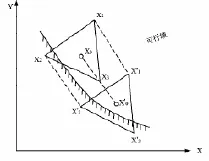
圖1 平移策略
平移步長H就是形心 X(0)與那個好頂點 X(L)的距離,即

平移點為
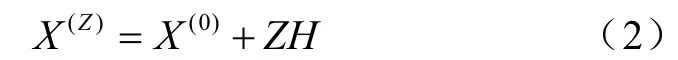
函數值為 F ( Z )= F( X(Z)),一旦平移成功,則按步長H繼續平移,直至平移失敗,退回最后一個成功點 X(Z),且把 X(Z)作為新正多面體的形心 X(0)。
如果可行頂點 X(L)的函數值 FL并不比形心函數值F0小時,則無法平移,而進入翻轉移動。若各頂點中無一是可行點,則進入收縮。
(2)翻轉:當正多面體所有可行頂點的函數值均比形心值F0大時,就準備翻轉。所謂翻轉就是,除某一頂點 X(U)外,正多面體的其他幾個定點不動,將 X(U)用其他n個頂點所決定的超平面對稱點X(W)來代替,形成一個新的正多面體(如圖2所示)。
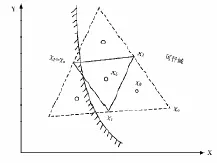
圖2 翻轉策略
翻轉后的新正多面體的形心 X(V)稱為原正多面體的旁心。顯然,一個正多面體有n+1個旁心,可以有n+1種不同的翻轉。
為實現最理想的翻轉,從n+1個旁心中找出函數值最小的可行旁心,記 X(V),其函數值記為FL。如果滿足

即旁心的函數值 FL小于原正多面體形心得函數值F0,則實施這種翻轉,并令 X(0)= X(V);否則,說明無法進行翻轉,只能實現收縮。
(3)收縮:當正多面體的各頂點均為非可行點或無法進行翻轉時,就實施收縮。將正多面體的各個頂點均向形心 X(0)收縮相同的距離,本文中收縮1/2,使形成的新正多面體的邊長T也相應收縮1/2,即

如圖3所示。
2 正多面體法的具體實現
(1)給定維數n,初始可行形心 X(0),初始邊長 T0和精度ε。 T0要取得適當,如果取得過大或者過小都會增加搜索時間。
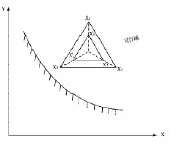
圖3 收縮策略
(2)形成初始正多面體:設形心 X(0)的坐標為函數值為 F0= F ( X(0))則n+1個頂點坐標可用兩維數組 X Y( i, j)表示如下,行號i為頂點號,列號j為該頂點的各維坐標分量。
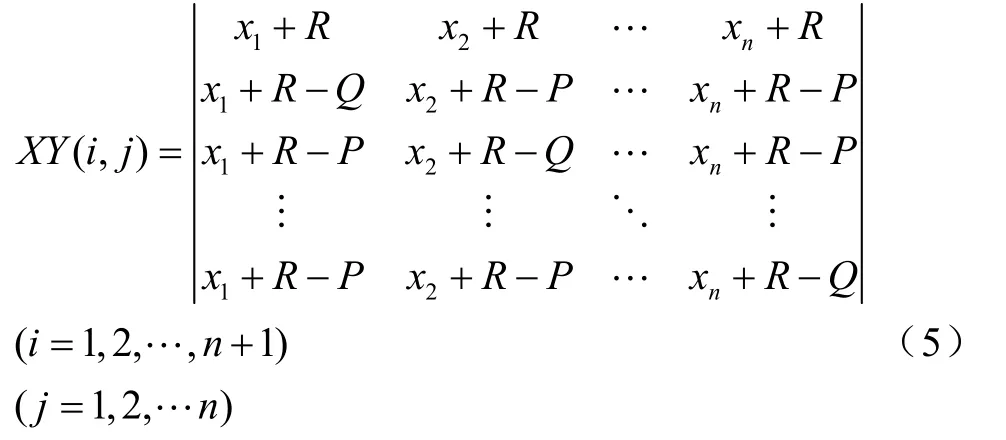
其中
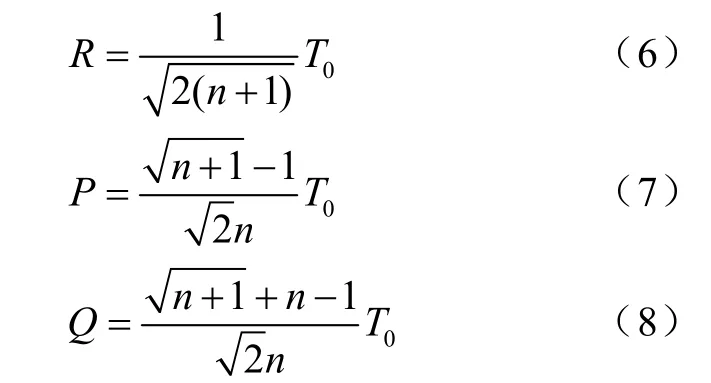
(3)判別正多面體的各個頂點是否均為外點。
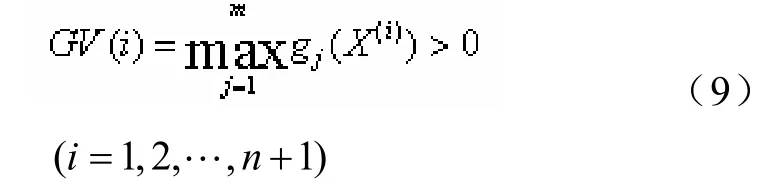
如果所有頂點都為非可行點,則轉式(9)進行收縮;否則轉式(4)。
(4)找出可行域中的最好頂點 X(L)

若滿足 F L<F0,則轉式(5)進行平移;否則轉式(6)找旁心。
(5)平移搜索:平移的方向是 X(0)→X(L),平移的步長為 H = X(L)- X(0)。對 Z=1,2,…,n,依次考察 X(Z)= X(0)+ ( Z + 1 )H , F ( Z )= F ( X(Z))。如果X(Z)是內點,且 F ( Z)<F0,即平移成功,繼續平移,且令 Z = Z+1, F0= F ( Z);否則,退回最后一個成功點作為形心,即
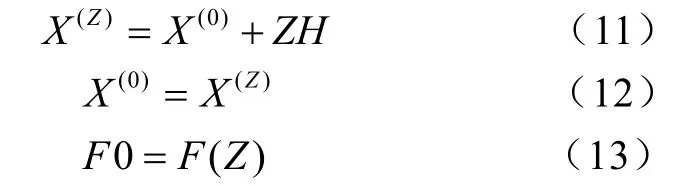
平移后形成的新正多面體的各頂點坐標為
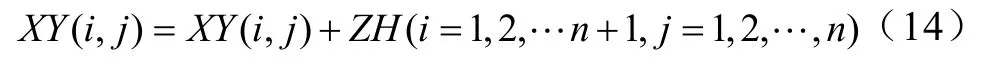
且轉式(3)。(6)計算各旁心,并判別是否均為外點?各旁心的坐標為
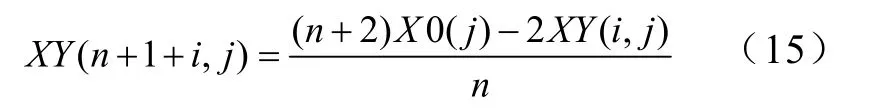
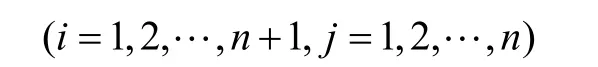
各旁心的約束函數最大值
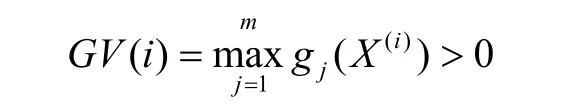
若各旁心均為非可行點,則轉式(9)進行收縮;否則找出最好的可行旁心 X(V),其函數值記為FL。
(7)翻轉判別:如果滿足 F L<F0,則轉式(8)實施正多面體的翻轉,否則式(9)進行收縮。
(8)翻轉計算:設翻轉前的形心為 X(0),頂點為 X(U),翻轉后的對應頂點為 X(W),翻轉后的新形心為 X(V),則
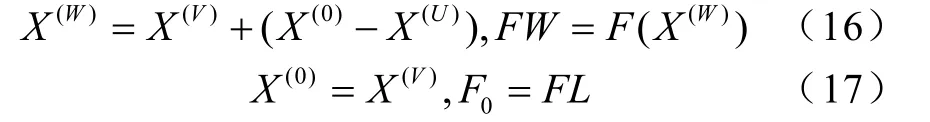
且轉式(3)
(9)收縮:當形成的正多面體的各頂點均為非可行點或者無法進行翻轉移動時,便實施收縮策略。將正多面體各頂點向形心 X(0)移動一半的距離,形成一個新的小正多面體。各新頂點的坐標為
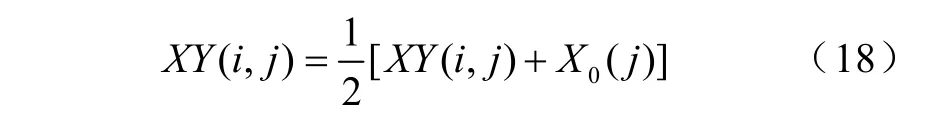
(i = 1 ,2,… ,n + 1 , j = 1,2,… ,n )邊長也減為一半,即

(10)終止迭代判別:如果正多面體的邊長滿足

此時,則輸出最優點
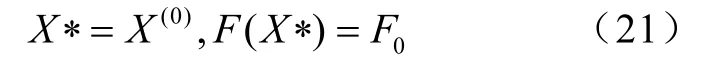
否則轉式(3)進行新的迭代。
3 軟件開發和算例分析
3.1 軟件的主要功能
(1)根據電機結構和尺寸計算其電磁特性、輸出轉矩、效率、輸出功率等力能指標以及溫升、損耗和有效材料成本。
(2)采用基于正多面體算法,以成本作為目標函數對電機的結構參數進行優化,并進行優化前后電機性能和成本的比較。
3.2 軟件的主題結構
根據軟件的主要功能,可分為兩個模塊,即電機電磁特性、性能、成本等計算模塊和優化算法模塊。模塊圖如圖4所示。
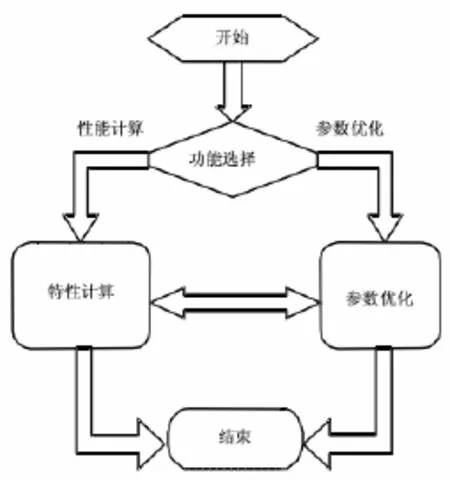
圖4 軟件模塊圖
3.3 算例分析
我們以有效材料成本為目標函數,采用正多面體優化算法對單相異步電機進行了優化設計。這里我們采用的電機仍為單相4極異步電機,額定轉速1500r/min,額定功率14W,電壓200V。具體結果如表1所示。
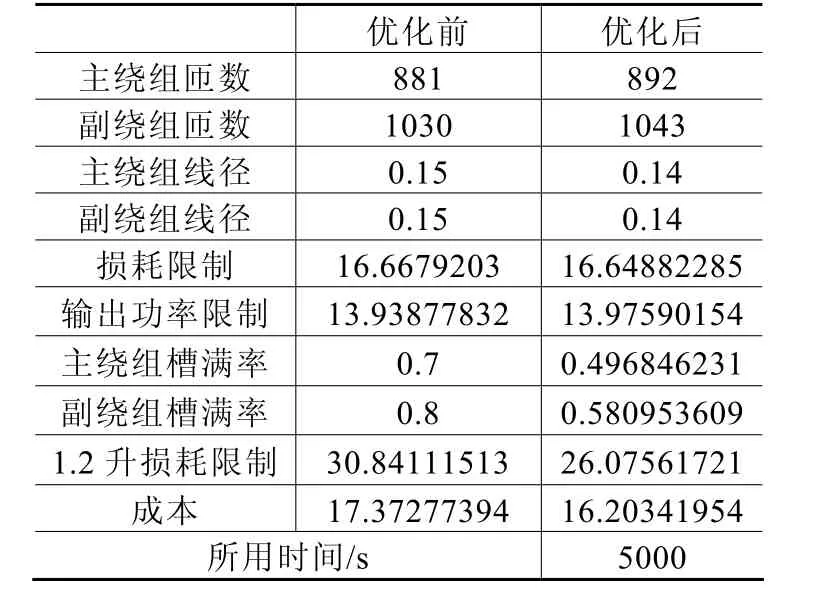
表1 參數對比分析
優化后,主繞組槽滿率下降了29.02%,副繞組槽滿率下降了27.38%,成本降低了6.73%。
4 結論
(1)正多面體算法程序簡單,控制量少,在搜索過程中只需要計算目標函數值,避免了因進行大量的目標特性分析、方法比較而造成的速度慢,計算量大,運算時間長等弊端。
(2)正多面體算法具有收斂迅速的優點,操作過程中不會產生大量的不可行解。
(3)正多面體算法適用于低成本,結構簡單的電機設計,可有效地降低成本,具有經濟實用性。
[1]俞鑫昌,電機、電器優化設計[M].機械工業出版社,1988.
[2]王充權,電機的計算機輔助設計與優化技術[M],上海:上海交通大學出版社,1989.
[3]Martin D W.Tee 1-1 J. Iterative methods for linear equations with symmetric positive definite matrices[J].The Computer Journal. 1961-1962(4).
[4]孟大偉,張弘,基于模擬退火算法及直接搜素法的混合優化策略在電機設計中的應用[J].電機與控制學報,1997, 1(2): 92-94.
[5]滿春濤,黃金杰,張筱磊,基于模擬退火算法的模糊控制器優化設計[J].電機與控制學報,2004,8(3): 281-284.
[6]Xi Ziqing and Zhou Keding. An improved simulated annealing algorithm and its application in global optimization of structure of a transformer core [C].Proc. of ICEF’2000,Tianjing 2000,322-324.
[7]Wang Youhua, Yan Weili et al. Adaptive simulated annealing for the optimal design of electromagnetic devices[J]. IEEE Trans. On Magnetics,1996, 32(3):1214-1217.
[8]Annakkage U D, Numnonda T,Pahalawaththa N C. Unit commitment by parallel simulated anneailng[J]. IEE Porc-Gener,Transm..Distrib,1995, 142(6):595-600.
[9]Cao Y J, Wu Q H. Optimal reactive power dispatch using an adaptive genetic algorithm[C]. Glasgow, UK:in Proceedings of Int. Conf. on Geneitc Algorithm in Engineeirng Systems,1997,117-122.
[10]Gomes J R, Saaverdra O R. Optimal reactive power planning using evolutionary Computation: Extended Algorithm[J].IEE Gen. Trans. and Dis,1999,146(6):586-592.
[11]張俊禮,葛斌,遺傳算法在壓水堆核電機組給水回熱分配中的應用[J],中國電機工程學報,2005,25(6):152-156.
[12]GARRET I H, LA IN . A knowledge-based system for designing transformers and inductors[C].IEEE Conference Proceedings, The 4th Conference. on Artificial Intelligence Application,1992.
[13]王育槐,吳建華,楊仕友,倪光正,多目標矢量優化的改進遺傳算法及其在電磁裝置優化設計中的應用[J],中國電機工程學報,2004,24(7):215-218.
[14]David C Walters,Gerald B Sheble. Genetic algorithm solution of economic dispatch with valve point loading[J].IEEE Trans on PS,1993,8(3): 1325-1332.
[15]楊仕友,倪光正,錢金很,電機電磁場逆問厄數值計算的改進Taba算法[J],中國電機工程學報,1998,18(4):83-86.

