基于變步長滯環比較法的MPPT算法研究

徐高晶 陳 婷 徐 韜

（1.國網電力科學研究院南京南瑞智源電氣技術有限公司，南京 210009；2.南京工業大學信息學院，南京 210009）

隨著社會的發展，能源和環境成為人們面對的緊要問題。太陽能作為一種廣泛分布的清潔可再生能源有很好的應用前景[1]，其中太陽能光伏發電技術得到了大量研究和應用，在光伏發電系統中，光伏電池的利用率除了與光伏電池的內部特性有關外，還受使用環境如輻照度、負載和溫度等因素的影響。在不同的外部環境下，光伏電池可運行在不同且惟一的最大功率點（Maximun Power Point，MPP）上。因此對光伏發電系統來說，應當尋求光伏電池的最優工作狀態，以最大限度的將光能轉化為電能[2]。

目前常用的實現MPPT的方法有導納增量法、擾動觀測法等。導納增量法是利用光伏電池在MPP處輸出功率對電壓的導納為零來跟蹤MPP，該方法控制效果好，控制穩定度較高，但是控制算法復雜，對采樣的精確度要求很高[3]。擾動觀測法是根據光伏電池的輸出功率的變化趨勢來擾動光伏電池的輸出電壓，使光伏電池最終工作于最大功率點。但振蕩和誤判問題的存在，使系統不能準確地跟蹤到最大功率點，造成了能量損失[2]。

綜上所述，以傳統擾動觀測法為基礎提出的變步長滯環比較法不但在克服最大功率點跟蹤過程中的振蕩和誤判方面均有較好的性能，且能兼顧到速度和精度的要求，更加準確地跟蹤光伏電池的最大功率點，從而提高光伏系統的發電效率。

1 光伏電池特性分析

1.1 光伏電池的等效電路

光伏電池實際上就是一個大面積平面二極管，可以用圖 1的單二極管等效電路來描述。圖中 RL是光伏電池的外接負載，負載電壓（亦即光伏電池的輸出電壓）為UL，負載電流為IL。

由圖1，可得負載電流IL為

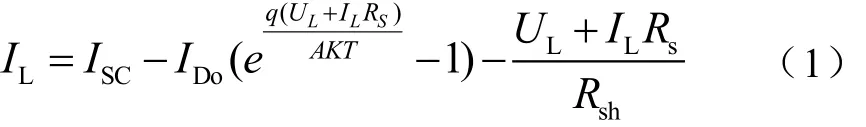
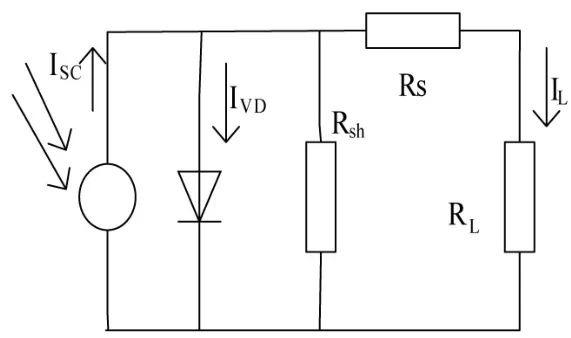
圖1 光伏電池的等效電路

式中，ISC為光子在光伏電池中激發的電流；IDO為光伏電池在無光照時的飽和電流；q為電子的電荷，1.6×10-19C；RS為串聯電阻（由電池的體電阻、表面電阻、電極導體電阻、電極與硅表面間電阻所組成）；A為一個常數因子（正偏電壓大時A值為1）；K為玻爾茲曼常數，1.38×10-23J/K；Rsh為并聯電阻（有硅片的邊緣不清潔或體內的缺陷引起的）。

1.2 光伏電池數學模型及輸出特性

一般光伏電池，串聯電阻 Rs很小，并聯電阻Rsh很大，在進行理想電路計算時可忽略不計，理想光伏電池的特性為

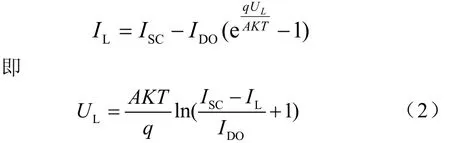
設在參考條件下，Isc為其短路電流，Uoc為其開路電壓，Im，Um為最大功率點電流和電壓，則當光伏陣列的電壓為Vpv時，其對應的電流為Ipv，根據光電池廠提供的 Im，Um，Isc，Uoc等參數就可以確定該光伏電池的輸出特性，但是由于廠商提供的這些參數一般是在標準溫度（Tref=25℃）和標準日照功率（Sref=1000W/m2）下的測試結果，在實際應用中還需要進行補償[4]，可以根據得到[2]

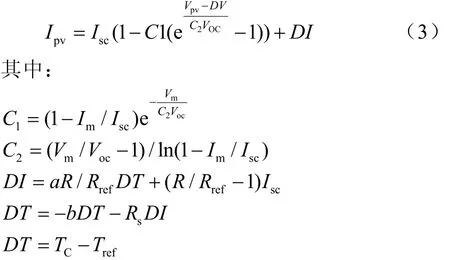
基于式（3），我們使用Matlab搭建了光伏電池的仿真模型如圖 2所示。參數為：電流變化溫度系數a=0.015Amps/℃，電壓變化溫度系數 b=0.700V/℃，Isc=5.45A，Uoc=22.2V，Im=4.95A，Um=17.2V。

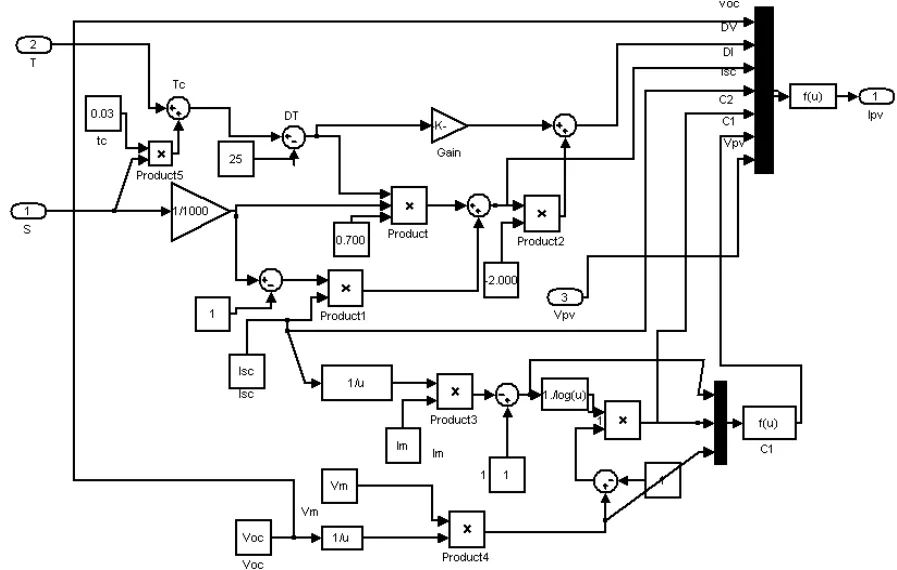
圖2 光伏陣列Matlab仿真模塊內部結構

封裝后的PV模塊如圖3所示。

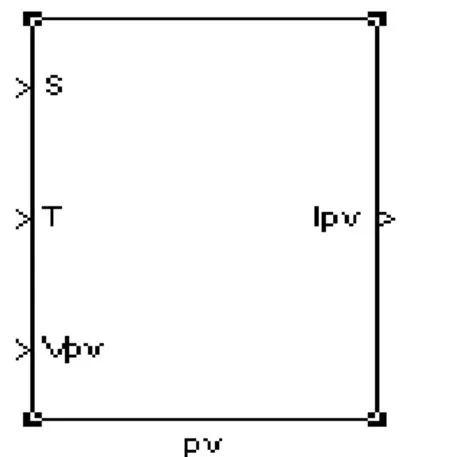
圖3 光伏陣列Matlab仿真模型封裝

模擬光照強度從 1000W/m2遞變到200W/m2時系統的輸出性能，如圖4所示。

由圖 4可知，光伏器件輸出功率 Ppv與輸出電壓Upv，電流Ipv呈非線性關系，在不同的環境即溫度，日照強度下，光伏器件存在唯一最大輸出功率點。當光伏器件置于室外環境時，由于外部環境不斷改變光伏器件最大功率也隨之改變。

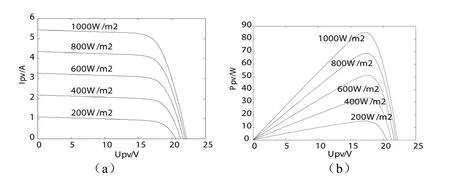
圖4 給定光照曲線下光伏陣列的輸出特性

2 變步長滯環比較法實現最大功率點跟蹤技術

工作點到達最大功率點附近時，對于定步長的擾動方式，會出現工作點跨過最大功率點的情形，但改變擾動方向后，工作點電壓與最大功率點電壓的差值還是小于步長，無法達到最大功率點，這種由于擾動步長一定所導致的工作點在最大功率點兩側往復運動的情形，就是擾動觀測法的振蕩現象。當外界環境發生變化時，光伏電池的輸出功率特性曲線也發生變化，會出現一段時間內工作點序列位于不同的Ppv-Upv特性曲線上的情形。此時對于不同的 Ppv-Upv特性曲線上的工作點繼續使用針對于固定特性曲線的判據，就會出現擾動方向與實際功率變化趨勢相反的情形，就是擾動觀測法的誤判現象。

2.1 變步長滯環比較法原理

從控制角度而言，抑制振蕩可以采用具有非線性特性的滯環控制策略，針對光伏電池的 Ppv-Upv特性，其滯環控制環節如圖5所示。

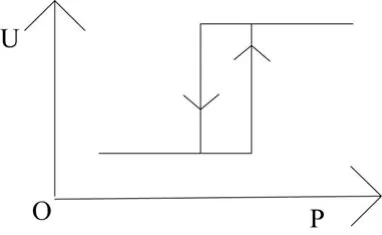
圖5 滯環技術示意圖

當功率在所設的滯環內出現波動時，光伏電池的工作點電壓保持不變，只有當功率的波動量超出所設的滯環時，才按照一定的規律改變工作點電壓。可見滯環的引入，可以有效地抑制擾動觀測法的振蕩現象。實際上可以將誤判看成是外部環境發生變化時的一種動態的振蕩過程，因此該方法也可以克服擾動觀測法的誤判現象。

2.2 系統功能的實現

雖然滯環比較法可以較大程度地避免振蕩和誤判現象，但如果步長過大，工作點可能會停在離最大功率點較遠的區域，如果步長過小，在新一輪開始搜索時，工作點會在遠離最大功率點區域內長時間地搜索，因此速度和精度的矛盾依然存在，采用變步長的滯環比較法便可以解決這一矛盾，具體流程圖如圖6。

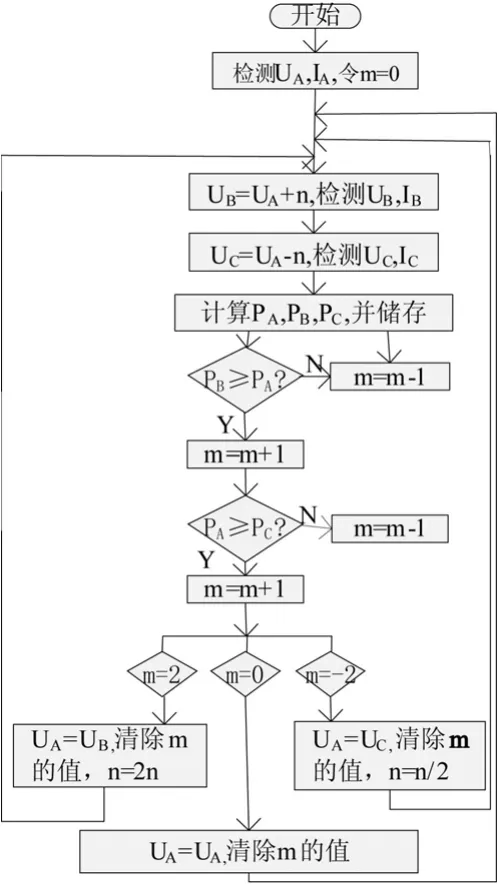
圖6 變步長滯環比較法流程圖

其原理如下：

在太陽能電池P-V特性曲線頂點附近從左至右依次取C，A，B三點，設變化標志m，擾動量為n，PC，PA，PB對應于 A，B，C 三點的功率，規定當 PB≥PA時，m=1，PB＜PA時，m=-1；當 PA≥PC時，m=1，當PA＜PC時，m=-1。這樣根據m的值就可以做出擾動方向的判斷。

（1）m=2，PB≥PA&PA≥PC，增加擾動量，增加步長，令n=2n；

（2）m=0，PC＜PA& PB＞PA，達到最大點；

（3）m=-2，PB＜PA&PA＜PC，減小擾動量減小步長，令n=n/2。

3 實驗結果分析

為了驗證所提出方法的正確性，把MPPT控制系統串入Boost變換器電路中，在Matlab/Simulink仿真軟件下搭建的仿真模型中，編寫 S函數作為MPPT的控制模塊，對光伏電池的最大功率點進行跟蹤，MPPT的仿真模型如圖7所示。為了形成對比，對采用擾動觀測法和變步長的滯環比較法MPPT控制方法進行了仿真。

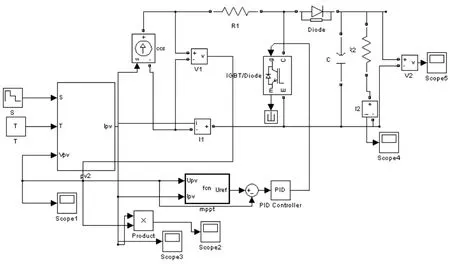
圖7 光伏并網Matlab仿真模型

根據圖7的光伏系統仿真模型，分別在MPPT模塊應用擾動觀察法和變步長的滯環比較法對外界條件變化后的某一瞬間進行仿真，如圖 8，圖 9所示。由圖8可以看出擾動觀察法在0.004s左右即可達到最大功率點，波形在往后的范圍內處于震蕩較明顯的情況。而圖9的變滯環比較法在0.00025s處即已達到最大功率點且波動比較小，說明變步長的滯環比較法的確在原來擾動觀察法的基礎上無論是從精度還是速度方面都有了一定程度的改進，從而提高了光伏系統的發電效率。

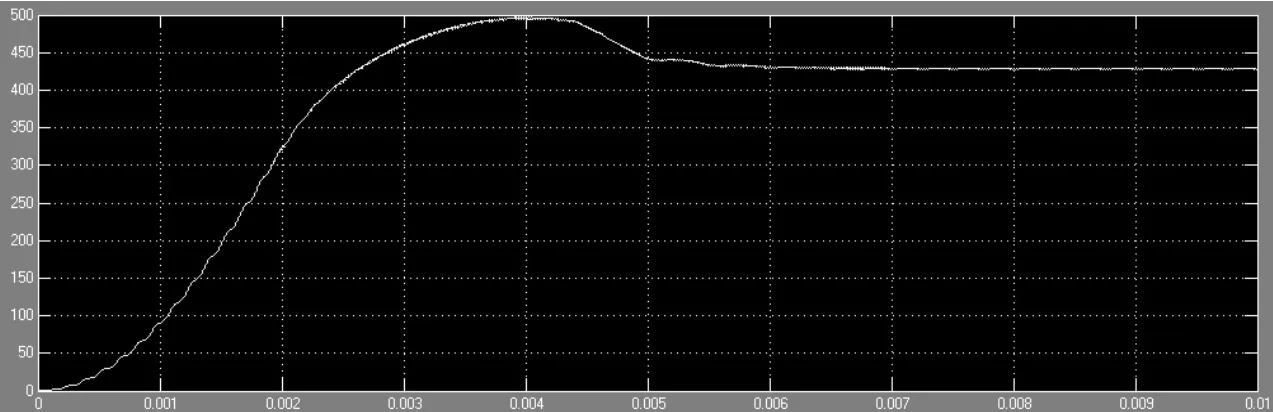
圖8 基于擾動觀察法的光伏電池輸出功率仿真波形圖

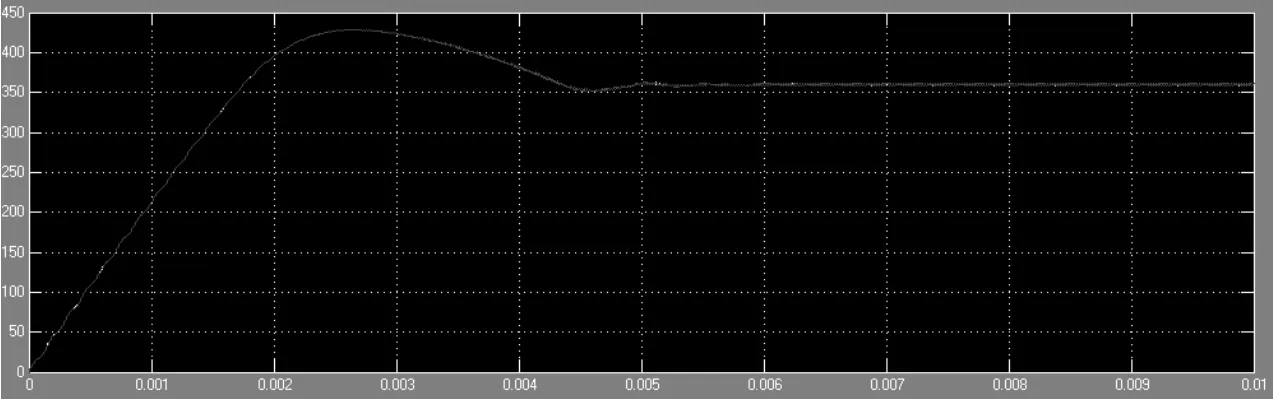
圖9 基于變步長的滯環比較法的光伏電池輸出功率仿真波形圖

4 結論

本文對光伏電池特性進行了詳細的分析，針對光伏系統的最大功率點跟蹤問題進行了研究，提出了基于擾動觀察法的變步長滯環比較法。變步長的滯環比較法的最大優點是通過雙向擾動確認的方法來保證擾動觀測法的動作可靠性，以避免誤判的發生，同時在搜索過程中不斷調整搜索的步長，也有效的抑制了最大功率點附近的振蕩。仿真結果表明，該算法具有很好的跟蹤速度和精度，是一種比較理想的控制方法，但是穩定性方面還需要改進。

[1]朱銘煉,李臣松,陳新等.一種應用與官府系統 MPPT的變步長擾動觀察法[J].電力電子技術,2010,44(1):20-22.

[2]張興,曹仁賢.太陽能光伏并網發電及其逆變控制[M].北京:機械工業出版社,2011.1.

[3]張超,何湘寧. 短路電流結合擾動觀察法在光伏發電最大功率點跟蹤控制中的應用[J].中國電機工程學報,2006,26(20):98-102.

[4]張建坡,張紅艷,王濤等.光伏系統中最大功率跟蹤算法仿真研究[J].計算機仿真,2010,1(27):266-269.

[5]張超,何湘寧,趙德安.光伏發電系統變步長MPPT控制策略研究[J].電力電子技術,2009,10(43):47-49.