股票價格運動的跳躍和杠桿效應研究

趙久偉, 肖慶憲

(上海理工大學管理學院,上海 200093)

股票價格運動的跳躍和杠桿效應研究

趙久偉, 肖慶憲

(上海理工大學管理學院,上海 200093)

基于已實現變差理論和雙冪次變差理論,在股票價格為半鞅過程的前提下將已實現波動率分解為連續波動部分和離散跳躍部分,研究了上證綜指收益率和波動率的杠桿效應以及連續波動部分和離散跳躍部分分別在杠桿效應中所起的作用,并且分析了跳躍部分和連續波動部分在價格運動過程中的區別.由獨立方程模型的估計結果發現各個模型擾動項之間存在著一種類似杠桿效應的非線性關系,然后再通過聯立方程組模型進一步驗證擾動項之間的內在依賴性.實證分析結果表明:收益率和波動率的杠桿效應主要是通過連續波動部分起作用.

雙冪次變差;內在依賴性;杠桿效應;聯立方程組

股票價格運動在金融市場中是一種復雜現象,尤其是股票價格波動規律引起了學者們的興趣.上世紀末以來,金融市場波動率的測量和建模在實證金融領域和時間序列計量經濟學領域一直是一個熱門專題.在國外,首先利用參數估計法對連續時間模型的研究工作可以追溯到Merton[1],此后,Andersen等[2],Chernov等[3]和Eraker[4]研究了帶跳躍的隨機波動率模型.但是基于日數據或者更高頻率數據的實證研究并沒有嚴格區分模型的擴散部分和跳躍部分,所以,跳-擴散模型的參數估計方法仍然沒有很好解決.近期一些文獻采用相對次高頻的日內數據測量波動率,如Andersen等[5]利用道瓊斯30只股票5分鐘收益率研究了個股波動率之間的相互依賴性.Barndorff-Nielsen等[6]引入非參數方法,發現高頻收益率的平方和收斂于價格過程的二次變差(quadratic variation),該測度包含了連續樣本路徑過程和跳躍兩部分的相關測度.Barndorff-Nielsen 等[7-8]將二次變差方法擴展到冪變差和雙冪次變差的非參數方法,認為當價格過程服從隨機波動模型時,價格過程的二次變差依概率收斂于連續波動部分與跳躍部分之和,從而能挖掘出其潛在的跳躍過程.Andersen等[9]利用非參數分解方法分析外匯現貨市場、證券期貨市場和利率期貨市場,并指出跳躍部分對價格方差有顯著貢獻.

國內學者針對已實現波動率理論做了大量研究.李勝歌等[10]利用深成指高頻數據對已實現雙冪次變差和已實現多冪次變差的有效性進行了研究,得出雙冪次變差在一般條件下比已實現波動率更有效.閔素芹等[11]和李勝歌等[12]研究了國內金融高頻數據最優抽樣方法理論.唐勇等[13]證明了在一定條件下已實現極差波動率優于已實現波動率,同時還研究了市場微觀結構噪音對波動率測量的干擾程度.苗曉宇[14]基于超高頻數據介紹了5種不同的風險度量方法.汪春峰等[15]基于雙冪次變差的測量理論,利用價格過程的非參數分解方法研究了我國上證綜指的已實現波動率和跳躍,結果發現已實現波動率的可測性均來自連續樣本路徑過程.綜觀上述研究工作,尚無文獻從已實現變差理論和雙冪次變差理論的角度闡述連續波動部分和跳躍部分在杠桿效應中所起的作用.

本文以上證指數為樣本,基于二次變差理論和冪變差理論將跳躍部分從價格過程中分離出來,嚴格區分連續樣本路徑方差和跳躍方差,進而檢驗兩種不同成分的統計特征,并在此基礎上建立收益率、連續波動部分和跳躍部分的離散時間模型,通過聯立方程組分析收益率與波動率之間的非對稱關系,以及不同成分對波動率的估計和杠桿效應的影響.

1 研究方法

1.1 兩個重要概念

在無套利的前提下,假設對數價格p(t)為半鞅過程,則連續時間跳-擴散過程可表示為

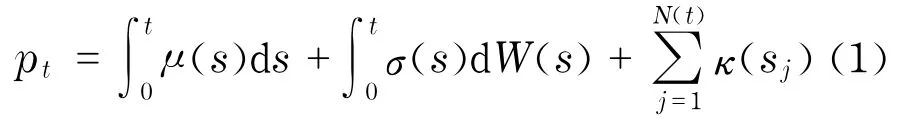
均值過程μ(t)是連續的局部有界變差過程,σ(t)＞0是右連左極(càdlàg)隨機波動率過程,W(t)是標準布朗運動,N(t)為跳躍次數,κ(s)表示跳躍幅度.則價格過程式(1)的二次變差可以表示為

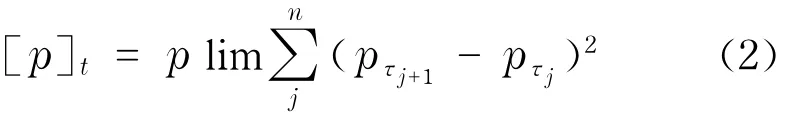
假設τ0=0≤τ1≤τ2≤…≤τm=t表示時間區間[0,t]的時間間隔,則當m→∞時有

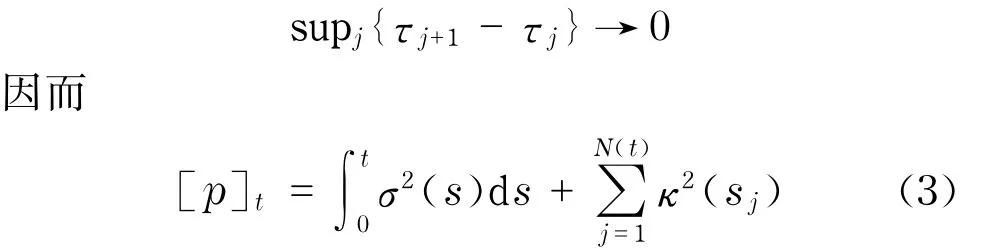
式(3)表示可積波動率與跳躍平方的和,其中,當跳躍的次數N(t)=0時,二次變差[p]t等于可積波動率∫t

0σ2(s)d s.

為了簡單起見,記第t天的收益率為

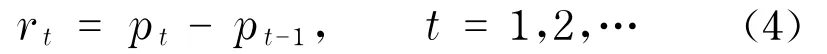
第t天的第j個日內收益率表示為

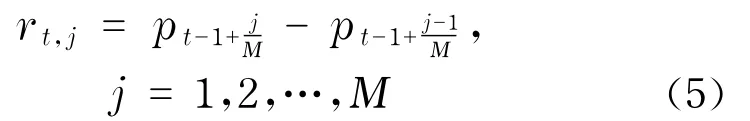
式中,M表示日內收益率的抽樣頻率,該收益率序列的平方和為

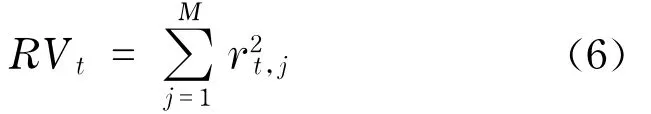
RVt為已實現二次變差的自然估計量(或稱為已實現方差,已實現波動率).特別的,當頻率M趨近于無窮大時,已實現波動率依概率一致收斂于二次變差

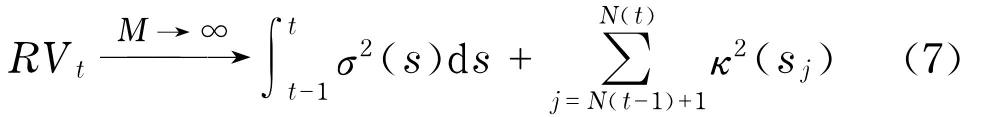
為了區別連續部分與跳躍部分,Berndorff-Nielsen等[7]第一次引入了雙冪次變差測度

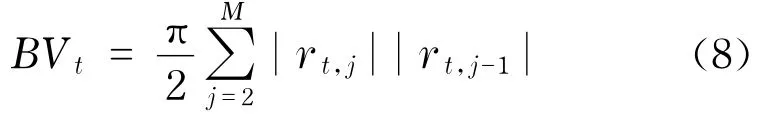
當抽樣頻率M趨近于無窮大時,雙冪次變差BVt一致收斂于可積波動率

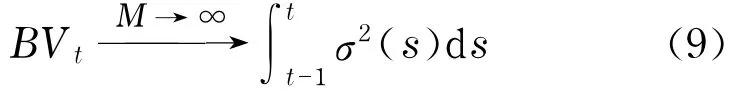
因此,已實現波動率和雙冪次變差的這種不同特點為整個價格變差過程中的跳躍部分提供了一種非參數估計方法.Huang等[16]提出了一種更強的(robust)跳躍測度

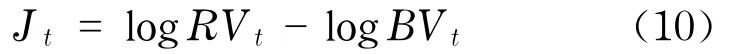
在實證研究中,本文依賴BVt和Jt的聯立模型解釋這兩種成分分別在日價格變差過程中的貢獻.跳躍測度Jt在理論上應該是嚴格非負的,然而,在實際操作過程中,由于抽樣頻率M有限,所以BVt可能會出現大于RVt的情況以至于造成Jt小于零.

1.2 基本模型

Corsi[17]提出異質自回歸模型(heterogenous autoregressive),即HAR-RV模型.Andersen等在文獻[9]和文獻[18]中應用該方法描述了雙冪次變差BVt的動態依賴性.Bollerslev等[19]提出了HAR -BV- GARCH模型作為HAR- RV模型的一種擴展形式,本文通過波動率的波動率模型(volatility-ofvolatility,即HAR- BV- GARCH模型)描述BVt模型中殘差序列的異方差性.考慮到對數雙冪次變差序列呈現出的長記憶性,定義多時期(multiperiod)雙冪次變差測度

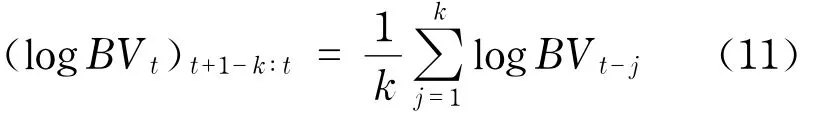
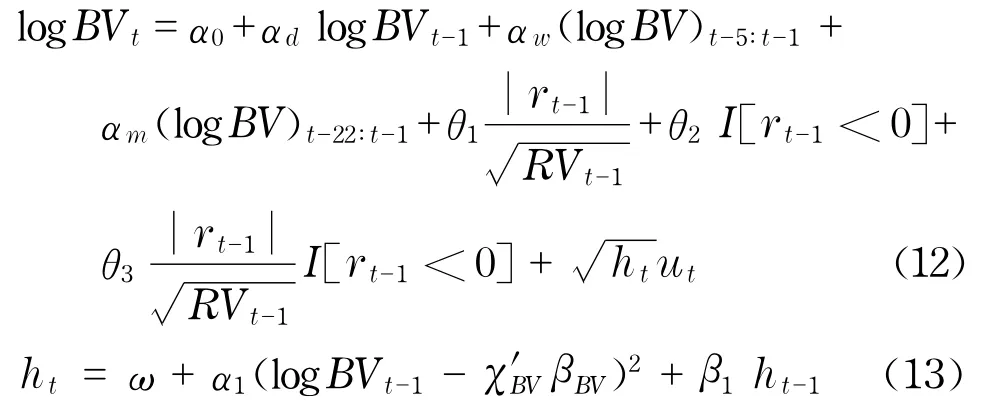
當k=5和k=22時分別表示一周和一個月,則雙冪次變差模型可表示為在此假設ut～N(0,1).式(13)中,χBV表示對數雙冪次變差模型的回歸元,βBV表示相應的系數.式(12)右端的第二項、第三項和第四項分別表示滯后一天、滯后一周和滯后一個月的雙冪次變差測度,而其余幾項則通過加入虛擬變量I來描述連續波動部分的杠桿效應.除此之外,Barndorff-Nielsen等[8]通過研究發現已實現波動率的波動對已實現波動率大幅度的變化反應程度不同,這也是本文采用HARBV- GARCH的主要原因.

其次,在跳躍模型中加入雙冪次變差模型中的杠桿項,形式為

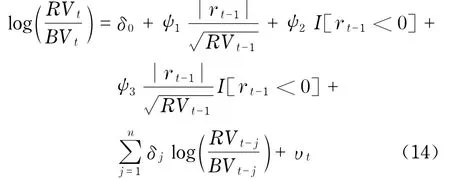
在此假設擾動項υt服從均值為0,方差為σ2的正態分布.眾所周知,股票收益率與波動率之間存在非對稱的負相關性,通過該模型使得我們可以偵查這種不對稱性是由于連續波動部分的作用還是跳躍部分的作用.

根據混合分布假說[20](mixture-of-distributions hypothesis),為了描述整個價格波動過程,考慮收益率模型

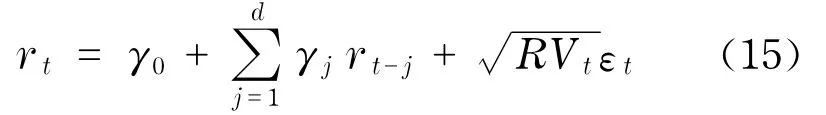
其中,日收益率依賴于已實現波動率測度RVt,εt服從標準正態分布.

2 樣本描述和單方程參數估計

雙冪次變差測度BVt和跳躍測度Jt的一致性取決于抽樣頻率M的大小,然而在實際中,抽樣頻率會受到實際報價和交易頻率等限制,以及高頻分時收益率可能受到市場微觀結構摩擦的影響,比如離散的價格采樣過程和買賣報價差(bid-ask spreads)等.此外,關于高頻數據最優抽樣頻率的選擇本身是一個熱點問題,不同市場的抽樣頻率選擇會有一些差異,一般來說5分鐘的抽樣頻率包含了較大信息量.本文選取2000～2009年上證綜指5分鐘數據作為高頻采樣數據進行研究,數據來自于萬得(WIND)金融數據庫(www.wind.com.cn).

上證綜指日收益率時間序列、對數已實現波動率序列、對數雙冪次變差序列以及跳躍序列如圖1(見下頁)所示,圖中所有序列均呈現出了明顯的波動率聚類效應(clustering effect),往往“大”的值的出現會造成這種異常值成群地出現.在跳躍時間序列圖中,可以觀察到大量的正觀察值,并且它們的值都很小.同時,這些觀察值中不乏還包含了負值,原因可以歸咎于價格過程的離散化和有限的抽樣頻率.

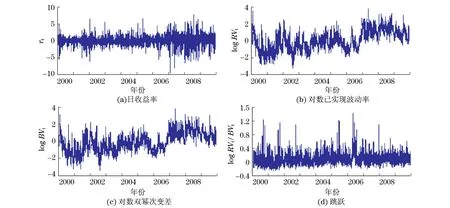
圖1 日收益率、對數已實現波動率、對數雙冪次變差和跳躍的時間序列圖Fig.1 Time series of daily returns，logarithmic realized variance，logarithmic Bipower variation and jumps

表1呈現的是本文相關序列的描述性統計分析指標.由表可見,已實現波動率序列的均值和標準差均大于雙冪次變差的平方根的均值和標準差,并且這兩種波動率序列的非條件分布均呈現出明顯的右偏和高峰特征.雖然這兩組序列存在明顯的右偏和高峰現象,但是,取對數后,偏度系數和峰度系數明顯下降,近似地服從正態分布.表中Q(10)表示滯后10階的Ljung-Box Q統計量.類似的,從表1和圖2可以觀察到跳躍測度Jt的描述性統計量以及相應的核密度分布圖清晰地顯示出正的偏度和尖峰態分布；日收益率序列的非條件分布也呈現出了預期的超額峰度和負的偏度.

表1最后一列顯示的為相關序列的LB統計量中,所有波動率序列均呈現出顯著的自相關,這同樣由圖3的自相關函數圖和偏相關函數圖得到證實.相比之下,圖3中收益率序列和跳躍測度沒有表現出如此強烈的自相關性,日收益率序列表現出1階滯后,而跳躍測度表現出5階滯后,也就是說當天的跳躍依賴于過去5天的跳躍.

表1 已實現波動率、雙冪次變差、跳躍和日收益率序列的統計量Tab.1 Descriptive statistics of logarithmic realized variance，logarithmic Bipower variation，jumps and daily returns

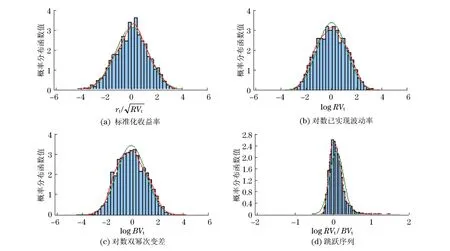
圖2 標準化收益率、對數已實現波動率、對數雙冪次變差和跳躍序列的無條件分布圖(實線)和核密度估計圖(虛線)Fig.2 Unconditional distributions of standardized returns，logarithmic realized variance，logarithmic Bipower variation and jumps

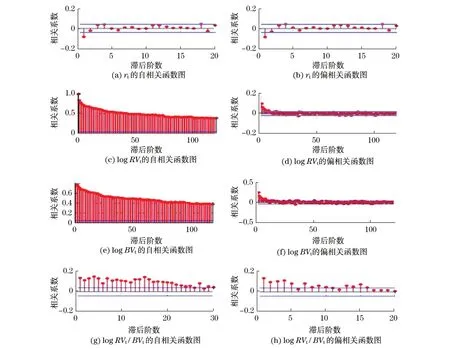
圖3 日收益率、對數已實現波動率、對數雙冪次變差和跳躍序列的自相關函數圖和偏相關函數圖Fig.3 Sample autocorrelations and partial autocorrelations of daily returns，logarithmic realized variance，logarithmic Bipower variation and jumps

雖然,已經得到了每個序列各自的序列相關性,但是,在聯立方程模型的建模中,序列之間存在的相關性以及依賴性則顯得更為重要.一些文獻提出了非對稱性的觀點,即“利空”消息相比“利好”消息會導致更大的波動率,過去的收益率擾動和現在的波動率之間存在負相關性,如Engle等[21]就提出了信息沖擊曲線(news impact curve)的觀點.Bollerslev 等[19]認為波動率的非對稱性主要是雙冪次變差序列BVt的非對稱性造成的.

如果模型之間的擾動項相互獨立,則每個模型的參數可以用最大似然方法單獨估計.但是,這種假設可能存在一定的問題[9],在此我們將獨立地估計每個模型以便檢驗這種假設的有效性.表2分別給出了雙冪次變差模型、跳躍模型和收益率模型通過Eviews計算出來的估計結果.

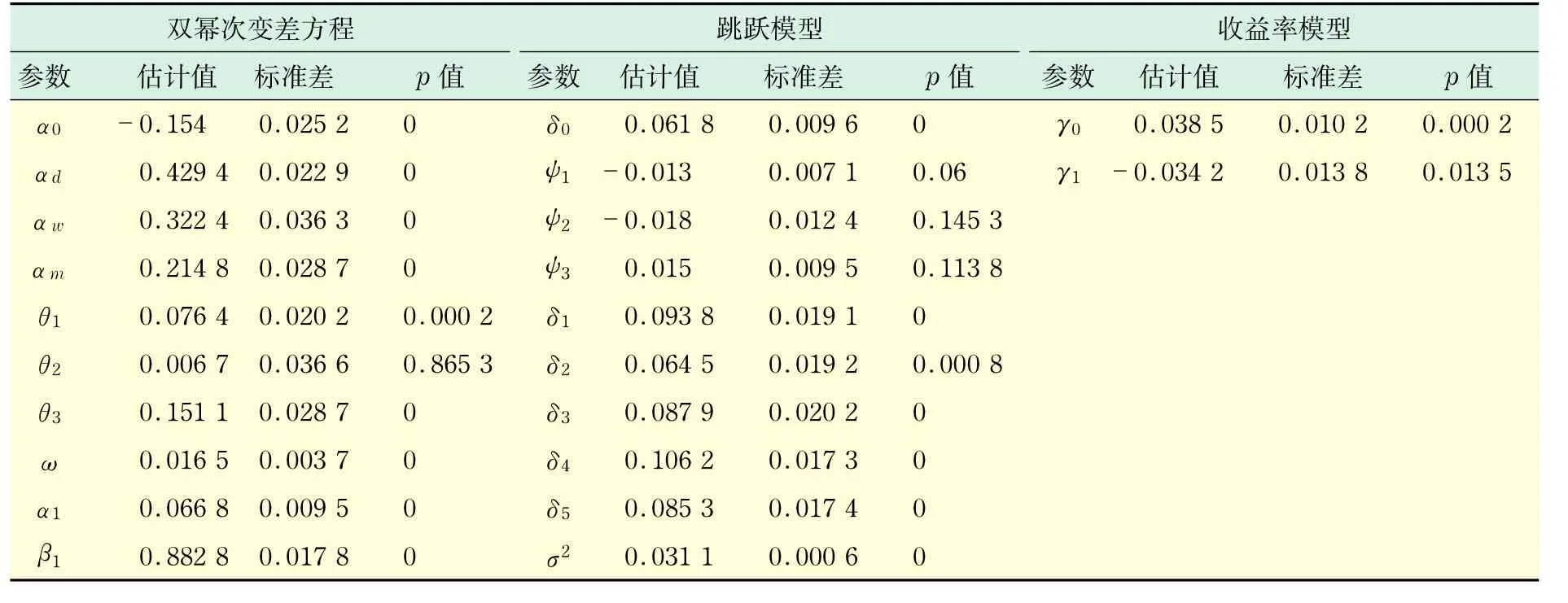
表2 獨立方程估計結果Tab.2 Single equation estimation results_______________________________

首先,從表2給出的雙冪次變差模型的參數估計結果中可以看到,αd、αw和αm的估計值分別為0.429 4,0.322 4和0.214 8,均為高度顯著的. GARCH(1,1)模型充分地刻畫了條件方差的變動過程,因為該模型的系數α1和β1的估計結果同樣顯著異于零,并且滿足穩定性條件α1+β1＜1.θ1和θ3則直接說明了連續波動部分的杠桿效應的確存在,與預期結論一致,相對于同樣大小的正的擾動,負的擾動會導致更大的波動率變化.相反,不顯著的θ2說明了負面新聞不能對波動率造成有效的影響.此外,殘差項的自相關函數和偏相關函數均沒有顯示出序列相關性.其次,跳躍模型的參數估計結果顯示,滯后1至5階的自相關參數估計量δj(j=1,2, 3,4,5)均顯著異于零,并且它們的值都很小,這與圖3的情況一致.同時,在表2中發現一個非常值得注意的情況,那就是解釋杠桿效應的參數ψ1、ψ2和ψ3的估計值均不顯著,也就是說跳躍沒有受到滯后1階的收益率擾動的非對稱影響,這與連續波動部分關于杠桿項的估計結果形成了鮮明的對比.最后,收益率模型中的參數估計值均顯著,滯后1階的自相關參數值也很小,γ1=-0.034 2.

3 殘差項的內在依賴性和聯立方程組

基于殘差項之間相互獨立的假設,3個模型的參數估計已經在上文中給出,但是這種假設的正確與否值得關注.我們知道,收益率方程和波動率方程中的擾動項存在相關性主要是因為杠桿效應或者波動率反饋效應.Bollerslev等[22]討論了高頻收益率的相關性,認為大樣本的高頻收益率能夠更精確地評價波動率的非對稱性.如果擾動項之間存在內在依賴性就會導致不一致的估計結果,但是,聯立方程組能夠解決這種依賴性并給出有效的估計結果[19].通過計算雙冪次變差方程、跳躍方程和收益率方程殘差序列的相關系數得到相關系數矩陣

雙冪次變差擾動項與跳躍擾動項和收益率擾動項均呈現出負相關系數,跳躍擾動項和收益率擾動項的相關系數較小.由于非對稱性的影響,擾動項除了存在線性關系還可能存在非線性關系,我們將通過擾動項ut、εt和υt的散點圖和非線性關系擬合以及核估計觀察非線性關系,如圖4.首先,ut和εt之間存在非對稱關系,這種關系類似于杠桿效應.其次, υt和εt之間的非對稱關系較弱.最后,υt和ut同樣顯示出了非對稱且非線性關系.通過圖形分析可以確定3組殘差序列的非對稱依賴關系的確存在,為了進一步檢驗殘差序列非對稱關系的顯著性和修正獨立方程估計的誤差,在此建立聯立方程組模型并將非對稱關系包含于模型內,所以,考慮聯立方程組模型

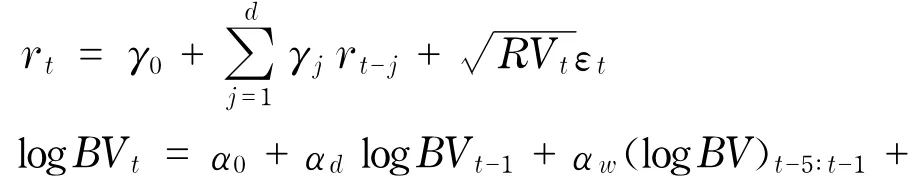
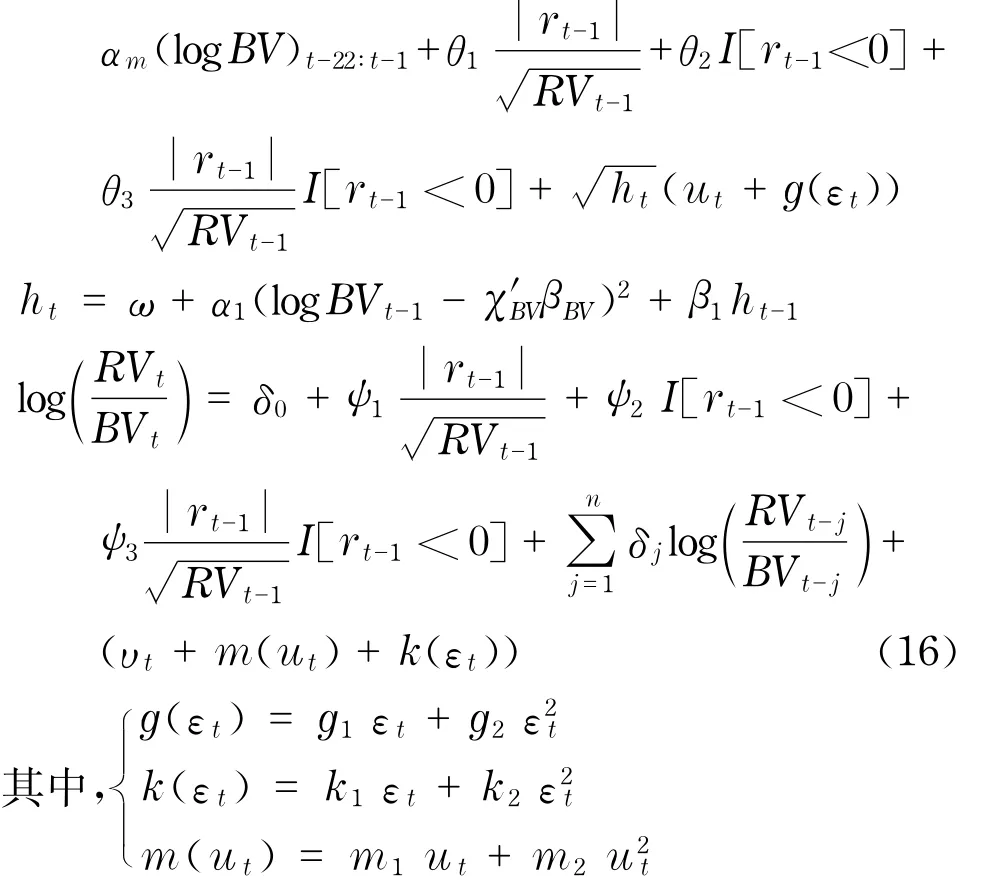
圖4 雙冪次變差模型、跳躍模型和收益率模型殘差序列之間的依賴性分析(虛線表示多元線性估計，實線表示核估計)Fig.4 Dependency analysis of the residuals among the return equation，Bipower variation equation and jump equation

與獨立模型相比,聯立方程組通過函數g(εt)、k(εt)和m(ut)使得連續波動率模型擾動項依賴于εt,跳躍模型擾動項依賴于εt和ut.鑒于此,考慮遞歸結構

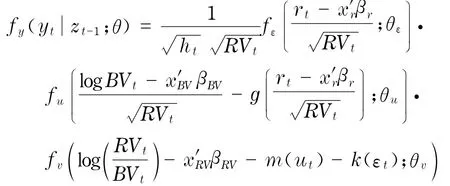
其中,yt=(log BVt,log(RVt/BVt),rt)′,zt-1為t -1時刻的信息集,xBV、xr和xRV分別表示對應模型的解釋變量,fε、fu和fv為殘差項的密度函數, 而θε、θu和θv表示密度函數的參數,εt、ut和vt分別服從N(0,1)、N(0,1)和N(0,σ2).聯立方程組的估計結果如表3(見下頁)所示,與獨立方程估計結果相比,大部分參數值沒有產生較大的變化.從表3中可以看到,杠桿效應依然存在并且與第2節中的推斷相一致.除此之外,高度顯著的參數g1和g2進一步說明了連續波動率方程殘差項和收益率方程殘差項之間的非線性關系.相反,對于跳躍方程和收益率方程殘差項的函數關系式k(εt),k1和k2均為不顯著參數.最后,參數m1和m2的顯著性進一步支持了連續波動率方程和跳躍方程殘差項的非線性關系.

從表3還可以看到,估計結果中還包括了其它幾個非顯著參數,限制非顯著參數的值為零,即θ2= ψ1=ψ2=ψ3=k1=k2=0,然后重新給出模型估計結果,如表4所示.通過對比表3和表4的估計結果發現,調整后的模型的估計結果沒有因非顯著參數限制為零而受到較大的影響,表4中的結果只表現出細微的變化.最后,還有必要診斷殘差序列ut、υt和εt之間的相關性.通過計算殘差序列的相關系數,得到相關系數矩陣和相關系數矩陣相比,矩陣中的數值更接近于0,換一個角度說,二次多項式成功地描述了殘差序列之間的非線性依賴性及其相互獨立的假設并不可靠.從估計結果可以看出,上證指數的杠桿效應主要通過連續波動部分起作用,通過聯立方程組模型可以抵消殘差序列的相互依賴性.

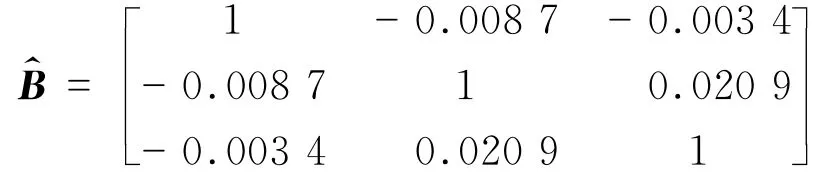
表3 聯立方程模型的參數估計結果Tab.3 Estimation results of the joint model

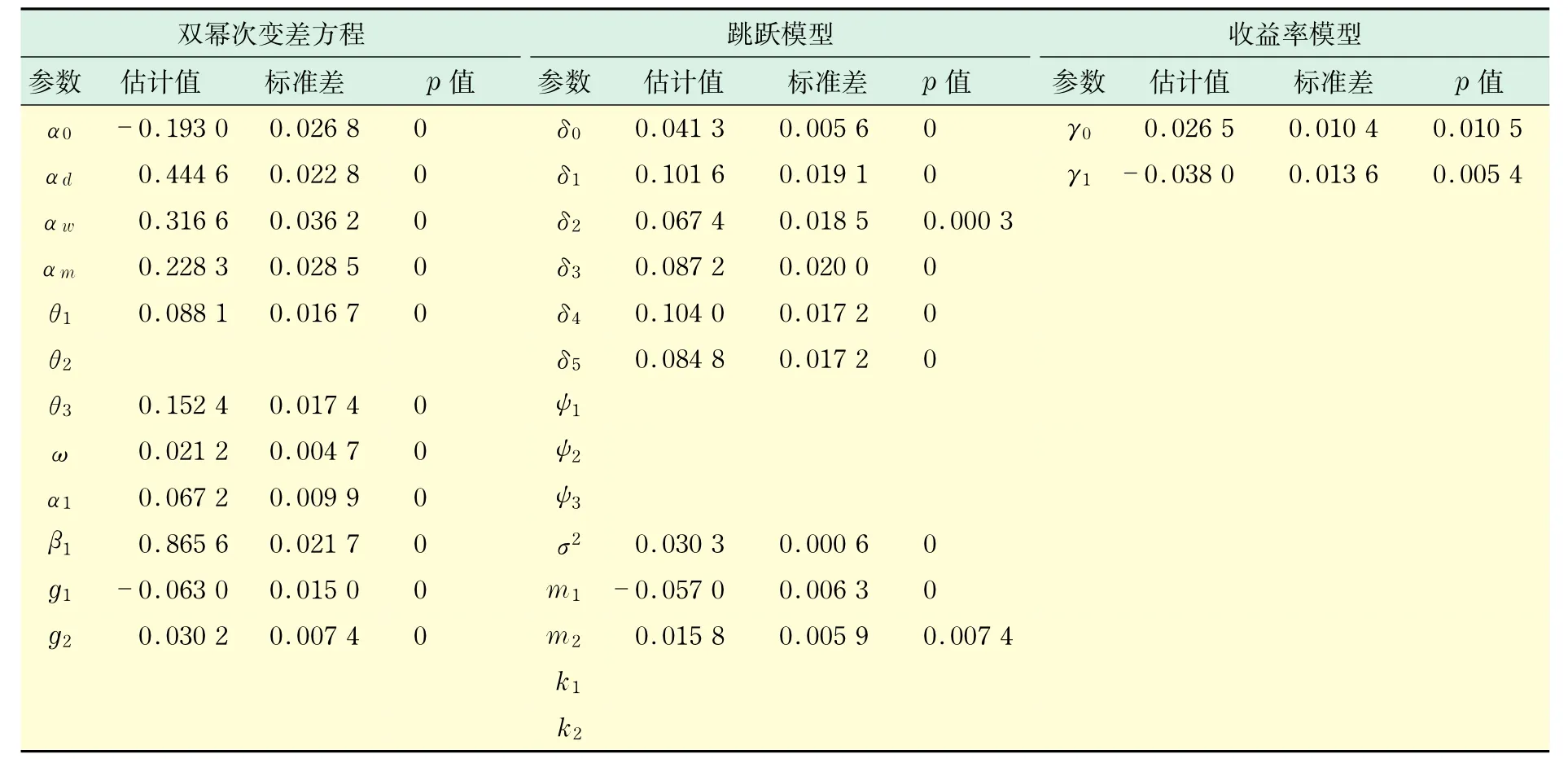
表4 剔除不顯著參數后的聯立方程模型的估計結果Tab.4 Restricted estimation results of the joint model

4 結 論

近幾年,波動率一直是實證金融研究和時間序列計量經濟學研究領域的一個熱點,因為金融資產收益波動率的估計和預測對資產定價、投資組合的選擇和金融衍生產品的設計起著至關重要的作用.采用“已實現”波動率測度和雙冪次變差測度作為市場波動率的度量方法,避免了較低頻率金融數據中復雜的參數估計,給其它參數波動率估計模型提供了一種間接的估計方法.

本文利用非參數分解方法將已實現波動率分解為連續波動部分和離散跳躍部分,基于已實現變差理論和雙冪次變差理論,在價格過程符合隨機波動模型的前提下,對上證綜指高頻數據進行分析得出以下結論:

a.通過聯立方程組建模,發現上證指數的杠桿效應主要通過連續波動部分起作用,而不是跳躍部分.

b.模型有效地檢驗了殘差序列之間的內在依賴性,同時指出殘差序列之間存在類似的非對稱現象.

c.基于高頻數據的“已實現”波動率測度和雙冪次變差測度衍生出價格變動的跳躍過程,通過建立關于波動率、跳躍和收益率的方程組模型,清晰地刻畫了連續波動部分和跳躍部分的動態特征并發現跳躍部分的持續性較差,跳躍部分的可測性弱于連續波動部分,因此,有效地改善了預測波動率的預測能力,這對波動率的區間預測和風險管理決策的研究意義重大.

[1] MERTON RC.On estimating the expected return on the market:An exploratory investigation[J].Journal of Financial Economics,1980,8(4):323-361.

[2] ANDERSEN T G,BENZONI L,LUND J.An empirical investigation of continuous-time equity return models [J].Journal of Finance,2002,57(3):1239-1284.

[3] CHERNOV M,GALLANT A R,GHYSELS E,et al.Alternative models for stock price dynamics[J].Journal of Econometrics,2003,116(1/2):225-257.

[4] ERAKER B.Do stock prices and volatility jump?Reconciling evidence from spot and option prices[J]. Journal of Finance,2004,59(3):1367-1404.

[5] ANDERSEN T G,BOLLERSLEY T,DIEBOLD F X,et al. The distribution of realized stock return volatility[J]. Journal of Financial Economics,2001,61(1):43-76.

[6] BARNORFF-NIELSEN O E,SHEPHARD N.Estimating quadratic variation using realized variance[J].Journal of Applied Econometrics,2002,17(5):457-477.

[7] BARNDORFF-NIELSEN O E,SHEPHARD N.Power and bipower variation with stochastic volatility and jumps[J].Journal of Financial Econometrics,2004,2 (1):1-37.

[8] BARNDORFF-NIELSEN O E,SHEPHARD N.How accurate is the asymptotic approximation to the distribution of realised variance[Z].Oxford:University of Oxford,2001.

[9] ANDERSEN T G,BOLLERSLEV T,DIEBOLD F X. Roughing it up:Including jump components in the measurement,modeling and forecasting of return volatility[J].The Review of Economics and Statistics, 2007,89(4):701-720.

[10] 李勝歌,張世英.“已實現”雙冪次變差與多冪次變差的有效性分析[J].系統工程學報,2007,22(3): 280-286.

[11] 閔素芹,柳會珍.“已實現”波動率中最優抽樣頻率的選擇[J].統計與決策,2009,13(13):13-15.

[12] 李勝歌,張世英.基于金融高頻數據波動率計算方法的比較研究[J].中國地質大學學報(社會科學版), 2008,8(1):80-83.

[13] 唐勇,張世英.已實現波動和已實現極差波動的比較研究[J].系統工程學報,2007,22(4):437-442.

[14] 苗曉宇.(超)高頻數據視角下金融風險度量研究進展[J].經濟論壇,2010,(8):202-207.

[15] 汪春峰,姚寧,房振明,等.中國股市已實現波動率的跳躍行為研究[J].系統工程,2008,26(2):1-6.

[16] HUANG X,TAUCHEN G.The relative contribution of jumps to total price variance[J].Journal of Financial Econometrics,2005,3(4):456-499.

[17] CORSI F.A simple long memory model of realized volatility[D].Lugano:University of Lugano and Swiss Finance Institute,2004.

[18] ANDERSEN T G,BOLLERSLEV T,HUANG X.A reduced form framework for modeling and forecasting jumps and volatility in speculative prices[J].Journal of Econometrics,2011,160(1):176-189.

[19] BOLLERSLEV T,KRETSCHMER U,PIGORSCH C,et al.A discrete-time model for daily S&P500 returns and realized variations:Jumps and leverage effects [J].Journal of Econometrics,2009,150(2): 151-166.

[20] FORSBERG L,BOLLERSLEV T.Bridging the gap between the distribution of realized(ECU)volatility and ARCH modeling(of the euro):The GARCH-NIG model[J].Journal of Applied Econometrics,2002,17 (5):535-548.

[21] ENGLE R F,NG V K.Measuring and testing the impact of news on volatility[J].Journal of Finance, 1993,48(5):1749-1778.

[22] BOLLERSLEV T,LITVINOVA J,TAUCHEN G.Leverage and volatility feedback effects in high-frequency data[J].Journal of Financial Econometrics,2006,4 (3):353-384.

Empirical analysis on jumps and leverage effect of equity price movements based on high-frequency data

ZHAOJiu-wei, XIAOQing-xian
(Busimess School,Umiversity of Shamghai for Sciemce amd Techmology,Shamghai 200093,Chima)

The leverage effect between returns and volatility of Shanghai Composite Index(SCI),was investigated and is was studied whether the observed so-called leverage effect is caused by a negative correlation between the lagged returns and the current continuous variance component and/or current jumps by using a nonparametric decomposition of the total price variation into two separate components based on the theories of realized variation and realized bipower variation.A discrete-time stochastic volatility model was introduced to distinguish the jump component and continuous volatility component of price movements. Then,a nonlinear relationship among the residuals was presented by use of univariate estimation results of the separate equations,which is similar to the commonly assumed lagged leverage effect.The modeling of the joint equation system allows to further assess the inter-dependencies among the residuals,and the estimation results of the joint model suggest that the leverage effect works primarily through the continuous volatility component.

bipower variatiom；imter-depemdemcy；leverage effect；joimt model

F 830文獻標示碼：A

1007-6735(2011)05-0499-09

2011-01-12

上海市重點學科建設資助項目(S30501)

趙久偉(1987-),男,碩士研究生.研究方向:數量經濟學.E-mail:zhaojiuwei28@126.com.

肖慶憲(聯系人),男,教授.研究方向:金融工程、數量經濟學.E-mail:qxxiao@163.com