動態結構化P2P網絡的負載均衡方案*

彭利民 肖文俊

(1.華南理工大學計算機科學與工程學院，廣東廣州510006;2.華南理工大學軟件學院，廣東廣州510006)

基于分布式散列表(DHT)的P2P網絡，通過采用統一的Hash函數將網絡中的對象和節點映射到一個鍵值空間，然后將資源按照鍵值存儲在鍵值相等或相近的節點上.由于Hash函數的隨機性，每個鍵值空間中的節點和對象分布也存在隨機性，因此，每個節點負責的對象個數也可能不同，文獻［1］中已證明:結構化P2P網絡中某些節點負責的標識符空間可能是其它節點的O(log2N)倍，N為P2P網絡的節點數.另外，P2P網絡中所有節點在分配存儲對象或負載時，不論其處理能力是否相同，都承擔著同樣的功能角色.現有研究表明:P2P網絡中節點的處理能力(包括存儲空間、帶寬及CPU性能等)具有很大的差異性［2］，容易出現某些處理能力較弱的節點承擔較高的負載，而處理能力較強的節點承擔較低的負載，使P2P網絡呈現負載不均衡問題.

負載均衡是一個經典且被廣泛研究的課題，文獻［3］中針對并行處理系統提出的負載均衡算法，有效地將單個處理任務有機地分配到多個處理器上，減少多處理器系統中單任務的執行時間.為實現分布式系統的動態負載平衡，文獻［4］中基于Multi-Agent提出了一種新的分布式系統動態負載平衡算法.根據節點間轉移虛擬服務器的思想，文獻［5］中針對P2P網絡的負載不均衡問題，提出了一對一、一對多和多對多負載均衡算法.文獻［6］中擴展了文獻［5］的一對多和多對多負載均衡算法，使其適應動態P2P系統.但文獻［5-6］中的負載均衡算法依賴系統中指定的d個目錄服務節點來收集負載信息和生成轉移策略，這種類似于集中式處理方式容易引起單點失效問題;而且在轉移負載時，由于沒有考慮節點間的物理位置關系，使負載均衡開銷增大，延緩了負載均衡操作的收斂時間.文獻［7］中通過在Chord系統上嵌入K-ary樹模型，并采用界標簇算法來收集網絡中節點的位置信息，使負載轉移盡量在物理位置較近的節點之間進行，從而減少轉移負載的物理跳數，節省系統資源.但K-ary樹的根節點需要定期收集所有節點的負載信息，并在將收到的信息分發給K-ary樹中各個節點后，模型中的節點才能確定自身的負載狀態.因此，在K-ary樹中某個父節點失效到其恢復前，其孩子節點所在子樹中的負載不均衡問題無法解決，并且每次負載轉移后，K-ary樹需要重新構造，使得構造和維護K-ary樹的開銷較大，P2P系統不便于擴展.在文獻［8］中，每個節點周期性地收集鄰近區域內其它節點的負載信息，并選擇鏈路延遲較小的節點轉移負載，但該方法只能保證局部的負載均衡，很難較快地使整個P2P系統達到負載均衡.

文中在超立方體P2P覆蓋網絡上構建一個基于二叉樹的負載均衡模型，根據節點的承載容量分配相應的負載，以減少負載均衡過程中的通信冗余和負載轉移開銷等.首先，將P2P系統中的節點組織成一個層次化的二叉樹型結構，負責收集與分發節點的負載信息，以減少負載均衡代價，并便于P2P系統的擴展.同時，通過引入均衡域概念，將P2P系統中的節點劃分到各個均衡域中，使負載均衡操作可以在整個系統或各均衡域中完成，有利于將整個P2P系統的負載均衡任務按照并行與分布式處理，降低負載均衡算法的時間復雜度，使負載均衡模型具有很好的適應性.

1 系統模型

1.1 相關概念和定義

(1)虛擬服務器.虛擬服務器是Chord系統中為改善節點負載量而提出的一個概念［9］，也是文中負載均衡處理的基本單位.虛擬服務器類似于P2P網絡中的節點，一個虛擬服務器負責相應的鍵值空間，而每個物理節點可擁有多個虛擬服務器.從負載均衡的觀點，虛擬服務器可以表示確定的負載量.當物理節點過載時，可以在其擁有的虛擬服務器中選擇一個或多個虛擬服務器轉移到其它非過載節點上.

(2)均衡域.均衡域是并行計算機系統中的一個概念［3］，通過將系統劃分為多個獨立的處理器集合(稱為均衡域)，可以將單個處理任務分配到多個處理器上，減少多處理器系統中單任務的執行時間.在圖2中，均衡域是指位于同一棵子樹中的節點集合，如節點000和001屬于同一個均衡域，節點000、001、010和011屬于同一個均衡域.均衡域的規模可以從幾個節點到整個系統，負載均衡決策唯一依賴于每個均衡域的負載狀態，各個均衡域可以并行地進行負載均衡操作，以減少整個系統負載均衡操作的收斂時間，降低負載均衡算法的時間復雜度.

(3)節點利用率.節點利用率是指節點的負載與承載能力的比值.節點的承載能力(綜合處理能力)可以是節點的CPU處理能力，也可以是節點的存儲空間大小.不失一般性，文中假定其為節點的存儲空間大小.通過引入節點利用率的概念，在負載均衡過程中可有效地處理P2P系統中的節點異構性問題，并按照節點的實際承載能力分配相應的負載，從而避免承載能力弱的節點承擔較高的負載量，使P2P系統中的負載均衡分布.

(4)均衡域利用率.均衡域利用率是指均衡域中所有節點的負載總量與總承載能力的比值.當整個系統屬于同一個均衡域中時，均衡域利用率表示系統利用率.根據均衡域利用率，可以在不同的均衡域內實施不同的負載均衡策略.

(5)海明距離.海明距離是計算機網絡通信理論中的一個概念，兩個碼字中對應位的比特值不同的位數，即為兩個碼字的海明距離.由于文中采用二進制數對超立方體P2P覆蓋網絡中的節點進行標識，因此，海明距離也可以用于表示節點間的最小距離.如節點 A(10001001)和 B(10110001)的第3、4和5位對應的比特值不同，其余的比特值均相同，因此，節點A和B之間的距離為3.一般將過載節點上的負載轉移到距離較近的節點上，以減少負載均衡的開銷.

1.2 基于二叉樹的層次負載均衡模型

超立方體結構具有較優的路由算法，其操作與維護簡單，因而是P2P網絡中一個較常用的覆蓋網絡結構，Pastry［10］、Tapestry［11］等都是基于超立方體結構的P2P系統.文獻［12］中提出的超立方體DHT覆蓋網絡，保持了覆蓋拓撲和物理拓撲的一致性，有效地支持P2P系統的文件共享.文中在文獻［12］的超立方體DHT覆蓋結構(見圖1)上，建立一個基于二叉樹的層次負載均衡模型(見圖2)，負責收集與分發P2P系統中的負載信息，以及執行負載轉移操作，以解決動態DHT網絡中的負載均衡問題.

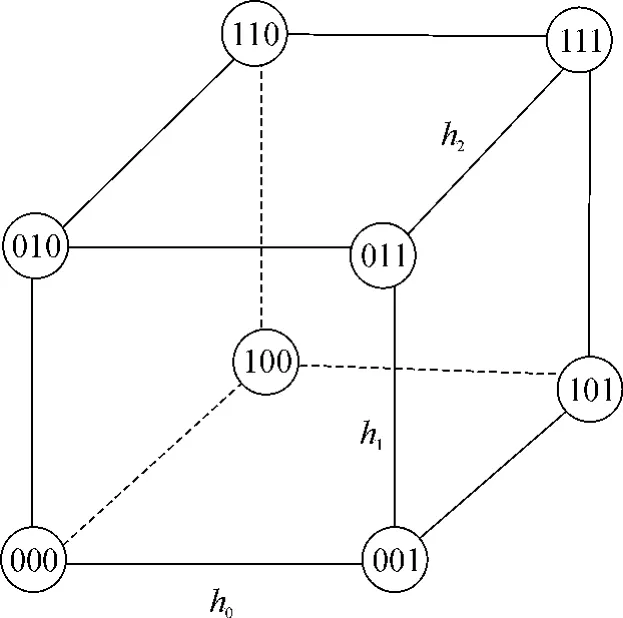
圖1 三維超立方體覆蓋網絡Fig.1 A 3-D hypercube overlay network

圖1中的h0、h1和h2分別表示超立方體的第0、1和2維度上的邊.二叉樹中的中間節點表示其下層相應均衡域中的域頭節點，這些節點負責收集自身均衡域內的負載信息以及控制均衡處理過程.例如，第1層的000、010、100和110節點分別負責第0層的2個均衡域(或節點)的負載均衡操作，第2層的000和100節點分別負責其管轄的第1層的2個均衡域的負載均衡操作，第3層的000節點負責其管轄的第2層的2個均衡域的均衡操作過程，按照這種自下而上的層次處理方法，該二叉樹模型將系統組織成一個層次的負載均衡域結構，分解了P2P系統的負載均衡處理過程.

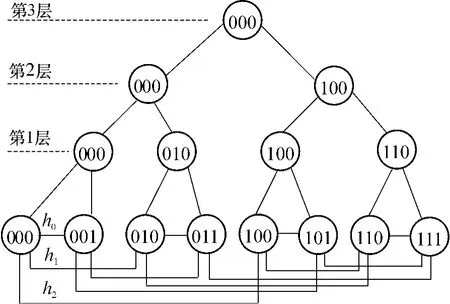
圖2 基于二叉樹的負載均衡模型Fig.2 A binary-tree based load balancing model

根據二叉樹負載均衡模型，可以按照自下而上的層次方法，在不同規模的均衡域內中實現負載轉移.例如，當節點000超載時，由節點000觸發負載均衡事件，由于節點000是由節點000和節點001組成的均衡域中的域頭節點，因此，節點000分析節點001是否可以用來轉移負載，如果可以，則將節點000上過載的負載轉移到節點001上，否則，按照自下而上的層次方法將過載負載轉移到第2層或第3層的均衡域內的節點上.另外，由于負載均衡操作可在不同層次的均衡域內進行，而且超立方體結構路由算法簡單，所以負載轉移易于實現，從而簡化負載均衡的操作過程，降低負載均衡的開銷和負載轉移代價.

2 分布式負載均衡算法

首先每個節點向其父節點發送負載信息，然后域頭節點計算每棵子樹(均衡域)的負載狀態并依次傳到樹根節點.當某個節點(或均衡域)的節點利用率超過預設的閾值，則觸發負載均衡事件.由于DHT網絡中節點的異構性，在設計負載均衡算法時，需要考慮節點承載能力的差異性，因此，文中根據節點利用率來計算需要轉移的超載量及確定可以接收超載量的節點(或節點集)，從而使分布式負載均衡算法便于處理異構DHT網絡中的負載均衡問題.

對于一個包含N個節點的P2P系統，負載均衡模型中第i層共有N/2i個均衡域.當所有均衡域內的負載都不均衡時(最壞的情形下)，每個均衡域內最多發送的負載均衡請求信息和負載轉移次數均為2i－1，則每層中負載均衡操作次數最多為N/2.由于二叉樹模型共有log2N層，因此，整個P2P系統中負載均衡操作次數最多為Nlog2N.由于P2P系統的均衡域可以按照平均并行度為N/2的并行方式執行負載均衡操作，因此，算法的時間復雜度為O(log2N).

3 仿真實驗與結果分析

實驗使用P2PSim作為模擬器來評估文中提出的負載均衡算法.為了便于比較，文中同時實現了文獻［6］中提出的負載均衡算法，表1列出了實驗參數值.實驗采用P2P系統中3個主要的標度進行測定，即節點利用率、負載轉移因子和負載轉移跳步數.其中，負載轉移因子是指負載均衡過程中的負載轉移代價與系統中所有負載轉移一次的總代價的比值［6］，它表示負載均衡過程中的負載轉移代價.負載轉移跳步數是指在負載均衡過程中，負載從超載節點轉移到輕載節點路由過程中的物理跳步數，它表示負載均衡開銷，負載轉移跳步數越小，負載均衡開銷也越小.每次模擬時間均為20T，其中，T表示預設的均衡周期.對于每個實驗情況進行10次實驗，取10次實驗結果的平均值作為該實驗的最終結果.

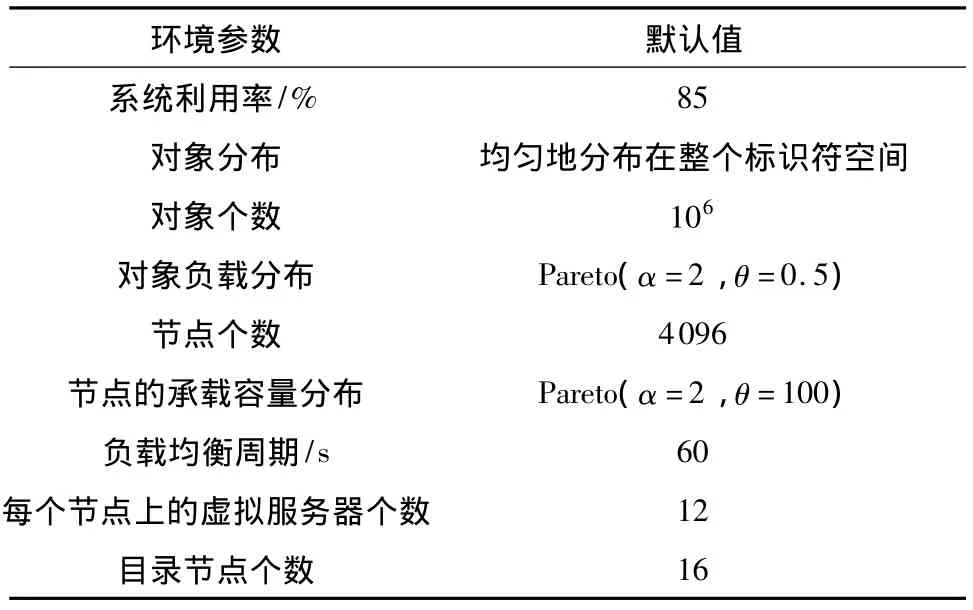
表1 實驗參數設置Table 1 Setting of experimental parameters

實驗1 測試在不同的系統利用率下，執行負載均衡后P2P系統中的節點利用率分布情況，結果如圖3所示.

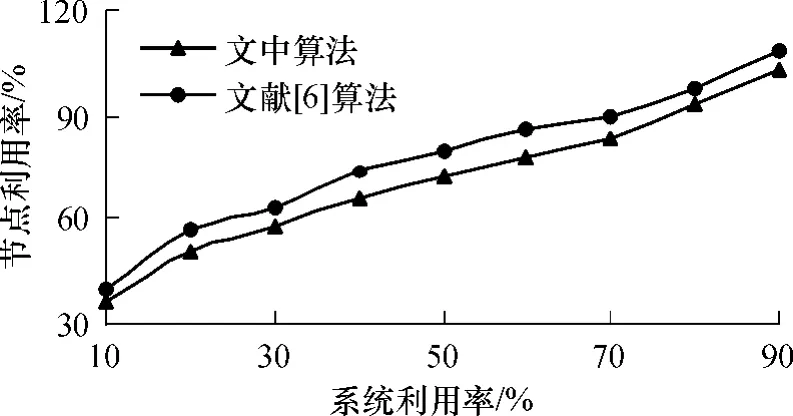
圖3 負載均衡后節點利用率分布Fig.3 Distribution of node utilization rate after load balancing

圖3表明:負載均衡后，兩種負載均衡算法的節點利用率隨系統利用率增加呈近似線性遞增趨勢，且負載均衡后的節點利用率略大于系統利用率.由于文獻［6］中的算法由多個目錄節點負責整個系統的負載均衡操作，各個目錄節點之間相互獨立，一個目錄節點管轄內節點上的負載無法轉移到另一個目錄節點管轄的節點中，因此，無法使整個P2P系統達到負載均衡.在文中提出的負載均衡方案中，各個節點按照均衡域的方式進行組織，且均衡域可以按照由下至上的層次結構進行擴展至整個系統，因此，可以使整個P2P系統達到一致性的負載均衡.從圖3可以看出，文中負載均衡算法的節點利用率均低于文獻［6］中算法的節點利用率，說明文中算法比文獻［6］中的算法能取得更好的負載均衡效果，當系統利用率為90%時，文中算法使網絡中93%的節點利用率低于100%，89%的節點利用率低于90%.

實驗2 測試在不同的系統利用率下，負載均衡過程中的負載轉移因子分布情況，結果見圖4.

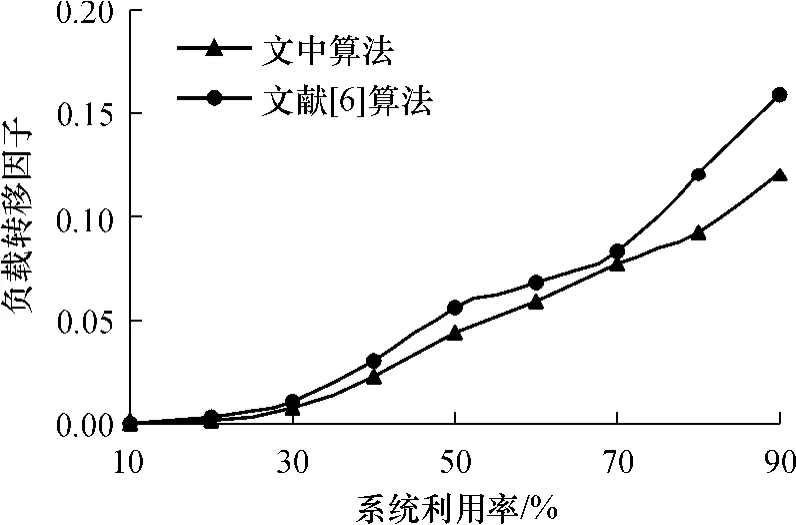
圖4 負載均衡過程中的負載轉移因子Fig.4 Load movement factor during load balancing

圖4表明:在不同的系統利用率下，兩種算法的負載轉移因子均隨系統利用率增加而增大，且兩種算法的負載轉移因子均較小，說明兩種算法在負載均衡過程中，只需要轉移較小的負載量就能使P2P系統中的負載均衡分布.由于文中的負載均衡算法以均衡域模式進行操作，負載均衡可以在局部范圍內執行，然后再擴展至整個系統;當某個節點超載時，文獻［6］中的算法首先隨機地選擇d個目錄節點，再由目錄節點在其管轄的節點范圍內執行負載均衡操作.因此，對于不同的系統利用率，文中的負載均衡算法總保持較好的性能，在系統利用率為90%時，文中算法的負載均衡因子小于0.13，而文獻［6］中算法的負載轉移因子約為0.17.

實驗3 測試負載均衡算法在P2P網絡動態環境下的負載均衡效果.主要考察額外的10%系統負載總量快速到達系統對負載均衡算法的影響，并將這額外的10%負載量隨機地分布在P2P系統的標識符空間上，額外增加的10%負載量不僅使節點的負載在短期內的分布更加不均衡，而且使P2P系統中節點承擔更大的負載量，結果見圖5.

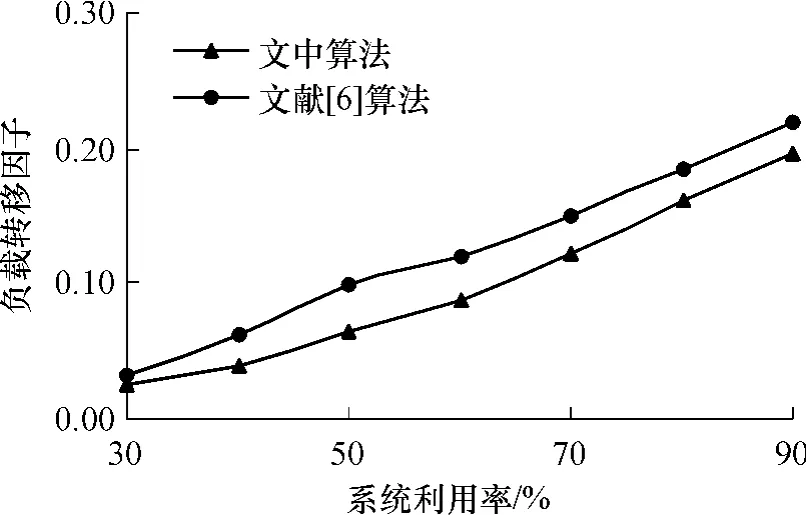
圖5 數據項動態環境下的負載轉移因子Fig.5 Load movement factor under dynamism of data items

圖5表明:負載轉移因子隨系統利用率增加而呈線性遞增.當系統利用率較低時，額外增加的10%負載只造成系統中少量的節點超載，兩種算法的負載轉移因子均較低.當系統利用率較高時，系統中大部分節點的可承載容量較小，額外增加的10%負載使系統中超載的節點數增加，因此，負載轉移因子增大.由于文中算法以均衡域方式執行負載均衡操作，各個均衡域規模可以根據負載狀態動態地進行擴展，因此，在各種系統利用率的情況下，文中算法的負載轉移因子均比文獻［6］中算法小.在系統利用率為90%時，文中算法的負載轉移因子小于0.20，而文獻［6］中算法的為0.22，表明文中算法能有效地解決動態P2P網絡環境下的負載均衡問題.

實驗4 測試負載均衡算法在節點動態進入/退出P2P系統情況下的負載均衡效果.P2P系統中節點總數固定為4096，每間隔1s有一個節點隨機地進入/退出P2P系統.為了評估負載均衡算法的動態適應性，文中將負載轉移因子定義為負載均衡算法所引起的負載轉移量與節點到達或離開而產生的負載轉移量的比值，結果如圖6所示.

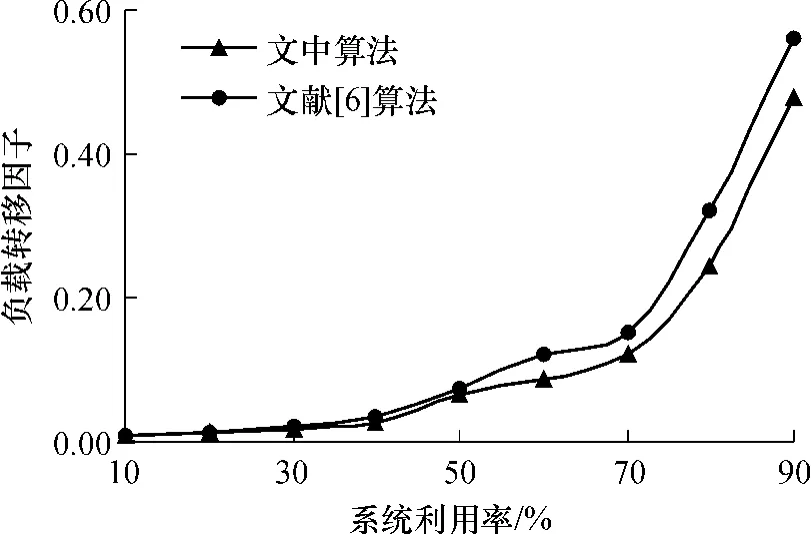
圖6 節點動態性與負載轉移因子Fig.6 Load movement factor under dynamism of node

圖6表明:負載轉移因子隨系統利用率增加而增大.當系統利用率較低時，兩種算法的負載轉移因子均較低，當系統利用率較大時，系統中節點的可承載容量較小，節點隨機地加入或退出使P2P系統中的節點負載狀態變化增大，需要轉移的負載量增多，因此，負載轉移因子增大.在系統利用率為90%時，文中算法的負載轉移因子小于0.50，文獻［8］中算法的負載轉移因子為0.56，表明文中算法能有效地解決動態P2P網絡環境下的負載均衡問題.

實驗5 測試負載均衡過程中轉移的負載在物理網絡上的跳步距離，以評估負載均衡算法的負載均衡開銷.

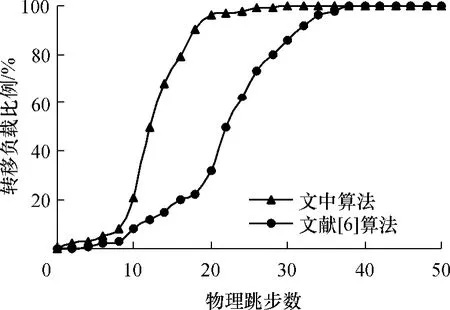
圖7 轉移負載的物理跳步數累積分布Fig.7 Cumulative distribution of moved load by physical distance hops

圖7顯示了兩種算法在負載均衡過程中負載轉移跳步數的分布情況.在文中的負載均衡模型中，各個均衡域按照節點的位置關系進行組織，而且在各個均衡域中分別地執行負載均衡操作，因此，超載節點和輕載節點都位于同一個均衡域內.當同一個均衡域中有多個輕載節點可用于轉移負載時，文中算法總選擇距離超載節點最近的節點進行負載轉移.在文獻［6］算法中，當P2P系統中某個節點k超載時，節點k在P2P系統中隨機地選擇目錄節點d，然后由目錄節點d負責執行負載均衡操作，由于目錄節點d在其管轄范圍內的輕載節點中隨機地選擇輕載節點h用于轉移負載，因此，過載節點k與輕載節點h相距離可能較遠.從圖7可以看出，文中算法使50%的轉移負載量在12跳內實現轉移，90%的轉移負載量在18跳內實現轉移，文獻［6］中算法在12跳內轉移13%的負載，18跳內轉移22%的負載量，50%的負載量在22跳內的節點間實現轉移.圖7的結果表明:文中算法能在鄰近節點間實現負載轉移，大大地降低了負載均衡的開銷.

4 結語

針對結構化動態P2P系統的負載不均衡問題，文中通過建立二叉樹負載均衡模型，提出了一種分布式負載均衡算法.仿真結果表明:文中提出的負載均衡算法不僅能解決不同系統負載狀態下的負載均衡問題，而且能有效地應對動態環境下負載的快速變化，有效地解決動態DHT網絡環境下的負載均衡問題.文中算法在負載轉移過程中，考慮了參與轉移負載的節點之間的位置關系，使負載在鄰近的節點間實現轉移，有效地降低了負載均衡的開銷.

［1］Karger D，Lehman E，Leighton T，et al.Consistent hashing and random trees:distributed caching protocols for relie-ving hot spots on the World Wide Web［C］∥Proceedings of the 29th Annual ACM Symposium on Theory of Computing.Texas:ACM，1997:654-663.

［2］Saroiu S，Gummadi P K，Gribble S D.A measurement study of peer-to-peer file sharing systems［C］∥Proceedings of Multimedia Computing and Networking.San Jose:SPIE，2002:156-170.

［3］Willebeek L H，Reeves A P.Strategies for dynamic load balancing on highly parallel computers［J］.IEEE Transactions on Parallel and Distributed Systems，1993，9(4):979-993.

［4］閆鈞華，張煥春，經亞枝.基于Multi-agent的分布式系統負載平衡［J］.華南理工大學學報:自然科學版，2004，32(12):74-79.Yan Jun-hu，Zhang Huan-chun，Jing Ya-zhi.Load balancing of the distributed system based on multi-agent［J］.Journal of South China University of Technology:Natural Science Edition，2004，32(12):74-79.

［5］Rao A，Lakshminarayanan K，Surana S，et al.Load balancing in structured P2P systems［C］∥Proceedings of the 2nd International Workshop Peer-to-Peer Systems.Berkeley:Springer-Verlag，2003:68-79.

［6］Godfrey B，Lakshminarayanan K，Surana S，et al.Load balancing in dynamic structured P2P systems［C］∥Proceeding of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies.Los Alamiws:IEEE，2004:2253-2262.

［7］Zhu Yingwu，Hu Yiming.Efficient，proximity-aware load balancing for DHT-based P2P systems［J］.IEEE Transactions on Parallel and Distributed Systems，2005，16(4):349-361.

［8］李振宇，謝高崗.基于DHT的P2P系統的負載均衡算法［J］.計算機研究與發展，2006，43(9):1579-1585.Li Zhen-yu，Xie Gao-gang.A load balancing algorithm for DHT-based P2P systems［J］.Journal of Computer Research and Development，2006，43(9):1579-1585.

［9］Stoica I，Morris R，Karger D R，et al.Chord:a scalable peer-to-peer lookup protocol for internet applications［J］.IEEE/ACM Transactions on Networking，2003，11(1):17-32.

［10］Rowstron A，Druschel P.Pastry:scalable，decentralized object location and routing for large-scale peer-to-peer svstems［C］∥Proceedings of the 18th IFIP/ACM International Conference on Distributed Systems Platforms.Heidelberg:Springer-Verlag，2001:329-350.

［11］Zhao B Y，Huang L，Stribling J，et al.Tapestry:a resilient global-scale overlay for service deployment［J］.IEEE Journal on Selected Areas in Communications，2004，22(1):41-53.

［12］Gharib M，Barzegar Z，Habibi J.A novel method for supporting locality in peer-to-peer overlays using hypercube topology［C］∥Proceeding of the 2010 International Conference on Intelligent Systems，Modelling and Simulation.Liverpool:IEEE，2010:391-395.