一種對MIMO雷達偵察識別的新方法
盛志超,盛驥松,楊 旋
(1.江蘇科技大學,鎮江212003;2.船舶重工集團公司723所,揚州225001)
0 引 言
多輸入多輸出(MIMO)雷達作為一種新體制雷達,通過分集技術在低截獲概率、目標參數估計、動目標檢測、雜波抑制、目標成像等領域的性能要優于傳統雷達,引起了雷達領域眾多科研工作者的廣泛關注。在現代戰爭條件下,電子對抗面臨的環境日趨激烈,以MIMO雷達為代表的新體制雷達給現代電子戰提出了新的挑戰,所以,急切需要研究具有針對性的偵察和對抗方法。
本文介紹了MIMO雷達的特點和常規的雷達信號分選方法,分析了它們對MIMO雷達信號進行分選的適用性,提出了一種采用奇異值分解和盲信號處理的方法對MIMO雷達進行偵察識別。
1 MIMO雷達的特點
20世紀90年代,MIMO技術在無線通信領域得到成功應用,它能夠克服無線信道產生的多徑衰落,改善信道的容量。由于通信系統和雷達系統的可比性,之后科研人員將其引入到雷達領域[1,2],采用多個發射和接收天線,在發射端發射的是一組正交信號,接收端每個陣元接收所有的發射信號并通過匹配濾波器組進行分選。
目前,各國的科研人員對MIMO雷達的研究主要基于2種模型,即共址MIMO雷達和分布式MIMO雷達,本文主要分析對共址MIMO雷達的偵察識別。
MIMO雷達的信號處理流程如圖1所示,主要特點有:(1)抗截獲性能提高,具有低截獲概率(LPI)優勢;(2)利用波形分集可以得到靈活的發射波束,提高檢測低速目標和微弱目標的能力;(3)通過發射正交信號具有虛擬陣元的優勢,產生較窄的波束和較低的旁瓣;(4)采用自適應技術獲得優異的分辨力。
MIMO雷達的信號處理流程如圖1所示。

圖1 MIMO雷達的信號處理流程
2 對MIMO雷達的偵察識別
2.1 常規的雷達信號分選方法
雷達信號分選是電子戰信號處理的重要組成部分之一,其基本原理就是從大量混疊的脈沖信號流中分離出各個雷達脈沖序列,并選出有用信號,以此分析各個雷達的特征參數。
常規的雷達信號分選由兩部分組成,即信號預分選和信號主分選。信號預分選根據瞬時參數到達角(AOA)、脈沖幅度(PA)、脈沖寬度(PD)和載頻(RF)等參數來稀釋脈沖信號流;接著,再利用到達時間(TOA)測量脈沖重復間隔(PRI)進行主分選。
可以發現,常規的雷達信號分選方法是按照串行規則進行檢測的,無法分選同時到達的多個信號。由于MIMO雷達同時發射多個相互正交的信號,因此接收機偵收到的信號是同時到達的混合信號,如果信號設計不嚴格,這些信號的頻域也會存在部分混疊現象。因此,常規的分選方法不能對偵收到的MIMO雷達信號進行有效的分選。
2.2 新的信號分選方法
針對常規的雷達信號分選方法無法勝任對偵收到的MIMO雷達信號的分選,本文提出了一種新的分選方法,它能夠對MIMO雷達信號進行有效的偵察識別,具體包括2步:第一,采用奇異值分解對MIMO雷達所發射信號源數進行估計;第二,根據所估計的信號源數采用盲信號處理中的算法對所偵收到的混合信號進行分離處理,由所分離出信號之間的相關性判定MIMO雷達是否存在。與常規的雷達信號分選方法相比,盲信號處理技術適應復雜的信號環境,能夠解決同時到達信號的分選問題。
2.2.1 對未知信號源數目的估計
在無噪聲時,如果傳感器數目大于信號源數目,并且信號源數據矩陣行滿秩,則信號源數目等于傳感器輸出的混合信號數據矩陣的秩數[3]。
當存在噪聲時,上述結論將不再成立。在實際

式中:Σ1=diag(σ1,σ2,…,σr),其對角元素按照順序σ1≥σ2≥…≥σr>0,r=rank(A)排列;O為0矩陣。
設σ1≥σ2≥…≥σr>0為矩陣A的奇異值,若存在正整數ε,使得任意的i≥ε和j≤ε,總有σj?σi,則稱ε為矩陣A 的主奇異值數[4]。
在有噪聲時,如果傳感器數目大于信號源數目,并且信號源數據矩陣行滿秩,則信號源數目等于傳感器輸出的混合信號數據矩陣的主奇異值數[3]。
具體的計算方法:對混合信號數據矩陣進行奇異值分解得到m個奇異值,去除最大奇異值σ1后,對剩余的按降序排列的奇異值進行如下運算:

則選取ε=k+1作為矩陣的主奇異值數,選擇的k滿足γk= max(γ1,γ2,…,γm-2)。
另外,在有噪聲時所采用的方法對無噪聲的情況同樣適用。
2.2.2 FastICA算法
盲信號處理包括3個主要方向:盲信號分離和提取、獨立分量分析(ICA)以及多通道盲解卷積和均衡。FastICA算法[5]由荷蘭赫爾辛基大學的科研人員提出,采用牛頓迭代算法,通過峭度的最大化得到偽逆矩陣W,算法的具體實現如下:
(1)對觀測信號x(t)進行去均值和白化;
(2)選擇初始化的隨機矩陣,W = [w1,w2,…,wn]T,令p=1,g(u)=uexp(-u2/2);
(3)令k=k+1,計算y(t)=wp(k)Tx(t);
(4)根據:的信號處理過程中,噪聲是不能免除的,因此,有必要考慮有噪聲時對信號源數目的估計。
根據 矩 陣 的 奇 異值分解[4],對 于 矩陣A ∈Rm×n(或Cm×n),則存在正交矩陣U ∈Rm×m(或Cm×m)和V ∈Rn×n(或Cn×n)使得 :

計算出 wi(k+1)。如果:‖wTi(k+1)·wi(k+1)-1‖ <ε,令p=p+1,否則轉到(3),直至p=n。
(5)y=Wx得到分離信號。
3 仿真實驗
MIMO雷達發射的是相互正交的信號,常見的有正交頻分線性調頻(OFDM-LFM)信號、正交多相編碼信號和正交頻率編碼信號等,這里僅考慮正交頻分線性調頻信號。
對MIMO雷達的偵察識別是基于信號之間的相關性來判別的,首先,判斷信號源數目;其次,通過盲信號分離算法估計源信號,對之做相關性處理來驗證信號之間的相關性,進而可以判斷是否是MIMO雷達。
為了驗證前述理論,筆者做了一些仿真實驗,實驗參數設置為 MIMO雷達發射3個OFDM-LFM信號,頻率間隔為3MHz,正交信號頻率起點為10MHz,采樣頻率為50MHz,LFM 調頻帶寬為3MHz,脈沖寬度為100μs,偵察接收設備有5個陣列,混合矩陣A為一5×3隨機矩陣,存在噪聲時,信噪比為10dB。
3.1 仿真1,對信號源數目的估計
在無噪聲時,觀測信號矩陣最大的奇異值為113.928 5,將之去除后所得的4個歸一化奇異值為σ2/σ2、σ3/σ2、σ4/σ2和σ5/σ2,從圖2可以看出觀測信號矩陣的非零奇異值有3個,而矩陣的秩數與非零奇異值個數相等,因此,在無噪聲時根據觀測信號矩陣的秩數就可以判斷出未知信號源數目。

圖2 無噪聲時的奇異值
在有噪聲時,觀測信號矩陣最大的奇異值為113.936 0,將之去除后所得的4個歸一化奇異值為σ2/σ2、σ3/σ2、σ4/σ2和σ5/σ2,從圖3可以看出觀測信號矩陣的非零奇異值有5個,根據2.2中的計算方法,如圖4所示,最大值即為k=2處,主奇異值數ε=k+1=3,因此可以判斷出未知信號源數目。
3.2 仿真2,對觀測信號進行盲信號分離并作互相關處理

圖3 有噪聲時的奇異值
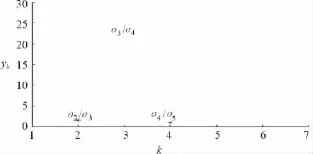
圖4 比值γk
信號源數目為3,源信號波形如圖5所示。在對混合信號經過FastICA算法分離后,盲信號處理結果如圖6所示,可以發現盲信號處理所分離出的信號順序與源信號順序不是對應的,這是由于盲信號處理的不確定性所造成的。接著,對分離出的信號進行互相關處理,從圖7可以看出它們滿足正交性,可以基本判定MIMO雷達的存在。

圖5 源信號波形

圖6 盲信號處理結果

圖7 信號互相關處理
4 結束語
本文將奇異值分解和盲信號處理應用到對MIMO雷達的偵察識別中,通過奇異值分解得到對MIMO雷達所發射信號源數目的估計,并且通過盲信號處理中的FastICA算法分離出MIMO雷達所發射的信號,通過互相關處理基本驗證了MIMO雷達的存在。
[1]Rabideau D J,Parker P.Ubiquitous MIMO multifunction digital array radar[A].Proceedings of Signals,Systems and Computers,Conference Record of the 37th Asilomar Conference[C].Pacific Grove,CA,2003,1057-1064.
[2]Fisher E,Haimovich A,Blum R,Cimini L,Chizhik D,Valenzuela R.Spatial diversity in radars-models and detection performance[J].IEEE Transaction on Signal Processing,2006,54(3):823-838.
[3]張洪淵,賈鵬,史習智.確定盲分離中未知信號源個數的奇異值分解法[J].上海交通大學學報,2001,35(8):1155-1158.
[4]張賢達.矩陣分析與應用[M].北京:清華大學出版社,2004.
[5]Hyvainen A,Oja E.A fast fixed-point algorithm for independent component analysis[J].Neural Computation,1997(9):1483-1492.

