基于流形排序的查詢推薦方法

朱小飛，郭嘉豐，程學旗，杜 攀

(1. 中國科學院 計算技術研究所, 北京 100190;2. 中國科學院 研究生院, 北京 100049; 3. 重慶理工大學 數理學院，重慶 400054)

1 引文

目前，互聯網上存儲了大量的信息，搜索引擎已經成為用戶訪問這些信息最有效的途徑。用戶通過輸入想要查詢的關鍵字到搜索引擎，然后搜索引擎返回搜索結果供用戶使用。然而，構造一個合適的查詢并不是一件輕松的事情，一方面因為查詢通常比較短[1](1～2個詞)并且存在歧義性[2](例如java，apple等)，另一方面，由于用戶對所查詢的內容不熟悉，使得自身對要查詢什么內容不清楚，例如用戶輸入harry potter，他可能是對名字叫harry potter的一款游戲感興趣，或者對同名的電影感興趣，也可能對同名的小說感興趣。如何幫助用戶更好的找到需要的信息已經成為一個至關重要的問題。

查詢推薦通過向用戶推薦相關的查詢，以幫助用戶構造更有效的查詢，目前已經成為一個十分重要的研究方向。一些著名的搜索引擎公司(如Google和Yahoo)開始為用戶提供查詢推薦系統，以幫助用戶更方便地找到所需要的信息。

傳統的查詢推薦方法主要關注于向用戶推薦相關的查詢，通過度量候選查詢與用戶所提交查詢的相關程度，對候選查詢進行排序，并推薦最相關的前k個查詢給用戶。這種方法可以有效地幫助用戶構造更恰當的查詢，但同時也存在一些問題：(1) 相關性度量問題。傳統查詢推薦方法通常在歐式空間上計算查詢之間的相似性，但由于查詢日志中的查詢具有高維稀疏性，傳統的相似度度量方法往往不能很好的反應用戶查詢之間的相關性。例如，在基于關鍵詞來度量查詢之間的相似性時，由于兩個相關的查詢(如“national basketball association”和“nba”)之間沒有相同的查詢關鍵詞，從而被認為是不相關；或者在基于用戶點擊的URL來計算查詢之間的相似性時，兩個相關的查詢因為沒有點擊相同的URL(因用戶結果點擊的稀疏性)，會導致其被認為不相關。(2)冗余性問題。由于僅關注候選查詢與源查詢的相關性，使得傳統的推薦方法所推薦的查詢存在較大的冗余性(推薦的查詢之間的差異性小)，例如當用戶輸入查詢“abc”時，系統可能會同時向用戶推薦“abc television”和“abc tv”，而這兩個查詢其實是表達了相同的意思。

為了避免傳統查詢推薦方法中存在的問題，已有研究人員提出一些解決方法，例如Mei等人[3]基于隨機游走(random walk)提出了通過計算各候選查詢到源查詢的游走時間(hitting time)來進行查詢推薦(文中使用Hitting-time Ranking來表示)，該方法可以有效地推薦長尾(long tail)的查詢給用戶，以降低查詢推薦的冗余性。然而通過這種方法獲得的長尾查詢往往不常見，相關性也無法得到保證，因此會影響到推薦的有效性和實用性。

針對已有查詢推薦方法的不足，我們提出了一種基于流形排序的查詢推薦方法(文中使用Manifold Ranking來表示)。通過把用戶查詢建模在流形結構上，我們可以利用查詢數據內在流形結構來獲得查詢之間的相關性，從而有效避免傳統方法的相關性度量問題。此外，基于查詢的流形結構，我們使用流形排序算法來對候選查詢進行排序和推薦，由于各查詢的排序得分不再僅來自于源查詢，同時也來自于其鄰居查詢，從而使得那些結構上與源查詢相近并且具有代表性的查詢(那些具有較多鄰居結點的查詢)獲得更大的排序得分。由此可見，和Hitting-time Ranking不同，Manifold Ranking是通過提升那些結構上具有代表性的查詢來減小查詢推薦的冗余性。

我們使用了一個大規模商業搜索引擎用戶查詢日志來進行實驗，該查詢日志包括約1 500萬條用戶查詢記錄。我們將Manifold Ranking與兩種基準方法：基于傳統的相似性排序算法(Na?ve Ranking)和Hitting-time Ranking進行比較，并通過一個自動評價機制來對各方法所推薦查詢的相關性和差異性進行評價。實驗結果表明，Manifold Ranking方法在保持較高相關性的條件下，明顯地提高了查詢推薦的差異性，在整體上要優于Na?ve Ranking和Hitting-time Ranking方法。

本文的組織結構如下：第2節介紹相關的研究工作，基于Manifold Ranking的查詢推薦方法將在第3節進行討論，第4節給出了實驗結果及其評價，結論將在最后一節給出。

2 相關工作

查詢日志作為一種用戶產生的數據，是眾多用戶在使用搜索引擎進行查詢操作時的日志記錄，其包含大量有價值的信息，被稱為“大眾智慧”(wisdom of crowds)[4]。近年來，許多研究工作開始使用查詢日志中的click-through data來挖掘查詢之間的語義相關關系，這種相關關系可以被用來進行查詢推薦。例如，Beeferman等人[5]通過對query-URL二部圖上使用凝聚聚類算法來發現相關查詢；Wen等人[6]同時考慮使用click-through data和查詢及文檔的內容信息來確定相似查詢。Li等人[7]提出了一個兩階段的查詢推薦方法：發現階段和排序階段。在發現階段，使用基于query-URL向量來計算查詢之間的相似度；在排序階段，使用層次凝聚聚類算法來對相似查詢進行排序。Baeza-Yates等人[8]基于query-URL二部圖定義了3種連邊類型：identical cover，strict complete cover和partial cover，并以此計算查詢間的語義關系。以上研究工作共同的特點是僅關注于推薦相關的查詢。Mei等人[3]在query-URL二部圖上使用隨機游走方法，依據各候選查詢到源查詢的游走時間來對查詢進行排序，可以有效的推薦長尾的查詢，但是其缺點在于：由于推薦長尾的查詢可能與源查詢相關程度不高，降低了查詢推薦的相關性。

Manifold Ranking是由Zhou等人[9-10]首先提出，與傳統的歐式空間上直接計算查詢之間的相似性不同，該方法通過利用大規模數據內在的全局流形結構來計算排序得分。直觀的解釋為：首先構造一個帶權網絡，并且分配給源節點一個正的得分，其他待排序節點的得分設為0，然后每一個節點將其自身得分傳播到鄰居節點直到整個網絡達到平衡狀態。除源節點外的所有節點按照最終得分大小進行排序(得分越大，排序越靠前)。目前Manifold Ranking已經被用來對圖像或文檔摘要進行排序，并取得很好的效果。例如，He等人[11]基于Manifold Ranking進行圖像排序，其利用所有數據之間的關系，來測量輸入查詢與所有圖片的相關性。Wan[12]等人使用Manifold Ranking來進行主題相關的多文檔摘要，通過利用文檔中所有句子相關性以及句子與主題的相關性，并基于貪心算法來實現有差異的文檔摘要。

3 我們的工作

在這一部分的內容中，我們詳細描述了如何使用click-through data來構造查詢的流形結構，然后在此基礎上使用Manifold Ranking方法來進行查詢推薦的過程。

3.1 基本概念

給定一組查詢χ={x0,x1,…,xn}?m，第一個查詢x0表示源查詢，其他查詢xi(1≤i≤n)為候選查詢。令d:χ×χ→表示χ上的一個度量，其中d(xi,xj)表示查詢xi和xj的距離(如歐式距離)。f:χ→為排序函數，其為每一個查詢xi(0≤i≤n)計算一個排序得分fi，這里我們可以將f看成是一個向量f=[f0,f1,…,fn]T。同時，定義向量y=[y0,y1,…,yn]T，其中y0=1(x0是源查詢)，yi=0(1≤i≤n)。

3.2 構造查詢的流形結構

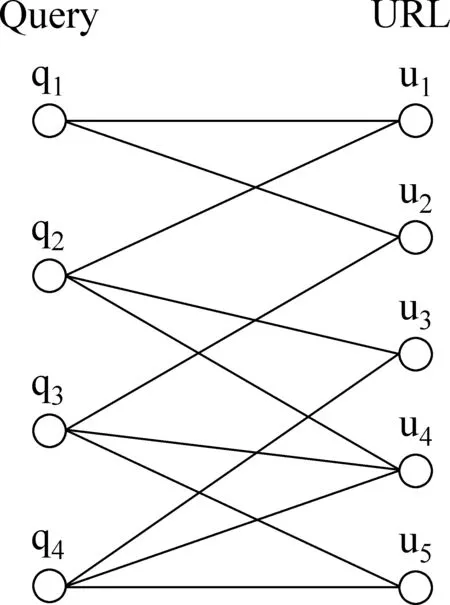
圖1 query-URL二部圖

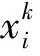
(1)

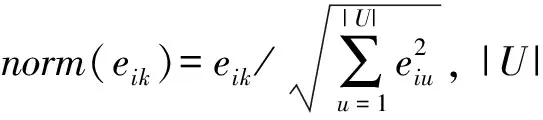
wij=e-d(xi,xj)2/2σ2

(2)

令wii=0。此外，若帶權網絡中邊所對應的兩個查詢不是互為k近鄰 (k=50)，則刪除此邊，以保持帶權網絡的稀疏性。至此，我們得到了一個查詢帶權網絡(即查詢流形結構)，其可以用一個仿射矩陣W=[wij]來描述。Manifold Ranking 算法如下：

1. Compute the pair-wise similarity valueswijbetween queriesiandj, and then construct a weighted network. The affinity matrixWis defined byW=[wij].

2. Symmetrically normalizeWbyS=D-1/2WD-1/2, in whichDis the diagonal matrix with (i,i)-element equal to the sum of thei-th row ofW.

3. Iteratef(t+1)=αSf(t)+(1-α)yuntil convergence, whereαis a parameter in [0,1), started withf(0)=0.

3.3 Manifold Ranking 方法

基于以上定義的查詢流形結構，我們使用流形排序算法來進行查詢排序和推薦。首先，我們對W進行對稱規范化：S=D-1/2WD-1/2，其中D為對角矩陣，其對角元素分別為W各行元素之和。然后，按照下面的迭代公式：

f(t+1)=αSf(t)+(1-α)y

(3)

迭代至f收斂。其中，α用來控制來自于先驗的得分和來自于結構上相鄰的結點得分對最終排序得分的貢獻，α值越大表示來自于相鄰的節點得分貢獻所占比例越大(α∈[0,1))。

Manifold Ranking的過程可以形象地描述為：首先構造一個帶權網絡，網絡中每一個節點對應于一個查詢；初始化時，給源查詢賦以一個正的排序得分，其余候選查詢的排序得分為0；網絡中所有的節點將其得分傳播給與其相鄰的節點，當網絡達到全局平衡狀態時，傳播過程停止；所有候選查詢的得分將被用來對候選查詢進行排序，并將排序最前的k個候選查詢推薦給用戶。Manifold Ranking算法的詳細過程，文獻[9]中證明了f最終會收斂到:

f*=β(I-αS)-1y

(4)

其中β=1-α，雖然可以直接使用(4)式來計算f*，但是由于涉及到計算逆矩陣(I-αS)-1，當數據規模較大時，需要的計算開銷很大，因此與大多數研究工作[10-11]一樣，我們這里選擇使用迭代方式來計算f*。

此外，為了減小計算開銷同時又不影響算法的有效性，我們從源查詢出發使用廣度優先搜索構造一個子圖，直到子圖中的查詢節點達到預先指定的數目。子圖的每一個節點(除源查詢節點外)可以看成是源查詢的一個候選查詢，那些不在子圖中的節點，由于離源查詢節點足夠遠，以至于不可能被推薦給用戶，將這部分節點去除，不會影響實際查詢推薦的效果，但可以有效的減小算法計算開銷。

4 實驗結果及評價

4.1 數據集

我們使用一個商業搜索引擎的查詢日志作為數據集，該查詢日志記錄了2006年5月1日至2006年5月31日期間的1 500萬條查詢。對于每一個查詢，日志中記錄其相應的信息，包括查詢ID，查詢詞本身，所點擊的URL，URL的位置信息，時間戳，用戶Session ID，URL在結果頁面中的排序，以及返回的結果數目。我們對查詢日志進行預處理：只保留英文查詢，并用空格替代查詢中的標點符號，不執行詞干還原和去除停用詞的操作。為了減小噪音數據帶來的影響，對于每個查詢要求用戶的點擊次數不能小于3次。表1是所獲得的query-URL二部圖的統計信息。

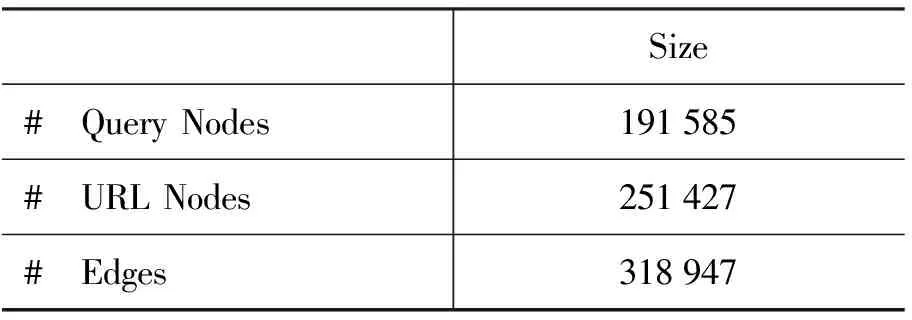
表1 query-URL二部圖的統計信息

4.2 評價指標

評價查詢推薦是一件十分困難的事情，因為對于一個查詢來說并不存在某種標準的推薦結果。為了使評價結果更為客觀合理，這里我們采用了一種自動評價的策略。該策略使用開放式分類目錄搜索系統ODP (the Open Directory Project)和Google的檢索結果作為評價數據資源，對查詢推薦結果的相關性和差異性進行評價。ODP是目前最大的人工編制的分類檢索系統，已經被一些研究人員用來作為評價數據，例如Baykan等人[13]使用ODP作為URL主題類別信息來評價分類結果，Baeza-Yates等人[8]使用其評價查詢的語義相關性。

4.2.1 相關性指標

對于ODP中的兩個類別ci和cj，我們定義其相關度為類別的相同前綴長度與類別最大長度的商，形式化的表示為s(ci,cj)=|l(ci,cj)|/max{|ci|,|cj|}，其中|l(ci,cj)|為類別ci和cj相同前綴長度，|c|為類別c的長度。舉例來講，兩個目錄“Arts/Television/News” 和“Arts/Television/Stations/North_America/United_States”的相關度為2/5。因為其相同前綴為“Arts/Television/”，長度為2，而最大類別為“Arts/Television/Stations/North_America/United_States”，長度為5。

對于每個查詢，在抓取Google Directory中前k個ODP目錄作為該查詢對應的類別集合，設C和C′分別為查詢q和q′所對應的ODP類別集合，類似于文獻[8]，我們用類別集合C與C′之間最相似的兩個類別的相關度來衡量查詢q和q′相關性。形式化表示為:

(5)

因此，對于給定的源查詢q，其推薦查詢結果的相關性指標定義為：所有推薦查詢與q的平均相關性，形式化表示為:

(6)

其中S為源查詢q的推薦查詢集合，|S|為推薦查詢集合中查詢數目。

4.2.2 差異性指標

對于每個查詢q，我們抓取Google前k個搜索結果的URL，作為查詢q對應的URL集合。查詢q和q′的差異度可以定義為：查詢q和q′的URL集合中相異的URL的數目所占的比例，形式化表示為：d(q,q′)=1-|o(q,q′)|/k，其中|o(q,q′)|是查詢q和q′的URL集合中相同URL的數目。因此，對于給定的源查詢q，其推薦查詢結果的差異性指標定義為：所有推薦查詢兩兩之間的平均差異度，形式化表示為:

(7)

其中S為源查詢q的推薦查詢集合，|S|為推薦查詢集合中查詢數目。

4.3 實驗結果及分析

我們隨機抽取了150個查詢作為測試樣本，類似于文獻[14]，我們要求這些查詢的各自總的URL點擊次數介于700至15 000次之間，這樣做的目的是為了避免選擇那些過于頻繁出現的查詢(例如www, car, book等查詢，因為對其進行推薦沒有實質意義)和過于不頻繁出現的查詢(查詢日志中不存在可以推薦的查詢)。其他參數設置為：算法迭代的次數設置為30, α=0.99, σ=1.25。

我們將基于Manifold Ranking的查詢推薦方法，與另外兩種查詢推薦方法(Na?ve Ranking，Hitting-time Ranking)進行了實驗比較，實驗結果分別顯示在表2和表3*注：我們沒有列出推薦數目為1的差異性指標，因為差異性指標是計算推薦查詢兩兩之間的平均差異度，當推薦數目為1時，計算出來的差異性指標沒有評價意義。中。表2是對三種不同方法的相關性指標進行比較，從表2中我們可以看到Manifold Ranking與Na?ve Ranking的查詢推薦結果在相關性指標方面接近相同(Na?ve Ranking的平均相關性指標為0.891，Manifold Ranking平均相關性指標為0.898)；而Hitting-time Ranking的查詢推薦結果在相關性指標方面要明顯低于前兩種方法(Hitting-time的平均相關性指標只有0.859)，這主要是因為Hitting-time Ranking方法過于強調推薦長尾的查詢，其計算候選查詢到源查詢的游走時間來作為推薦依據，而忽略了這樣一個事實：候選查詢到源查詢的游走時間的值小，并不意味著源查詢到候選查詢的游走時間的值也小，這就造成推薦的查詢與源查詢相關性不高。表3是對三種不同方法的差異性指標(所推薦查詢的冗余性越大，其差異性指標越低)進行比較，從表3中我們可以看到Manifold Ranking與Hitting-time Ranking的查詢推薦結果在差異性指標方面要顯著高于Na?ve Ranking方法(Hitting-time Ranking與Manifold Ranking的平均差異性指標比Na?ve Ranking方法分別提高了 4.9 和2.1個百分點)。從差異性指標比較的結果來講，Hitting-time Ranking要優于Manifold Ranking的推薦結果。但是如前面分析的結果所示，Hitting-time Ranking的平均相關性指標比Na?ve Ranking低了3.9個百分點，而Manifold Ranking平均相關性指標和Na?ve Ranking基本相同。從查詢推薦的角度來講，我們希望所推薦的查詢與源查詢盡可能相關，同時所推薦的查詢之間又盡可能保持差異性。考慮查詢推薦的相關性與差異性，我們可以得到以下結論：Manifold Ranking其在不損失相關性的條件下，明顯的提高了查詢推薦的差異性，整體上要優于Na?ve Ranking和Hitting-time Ranking。

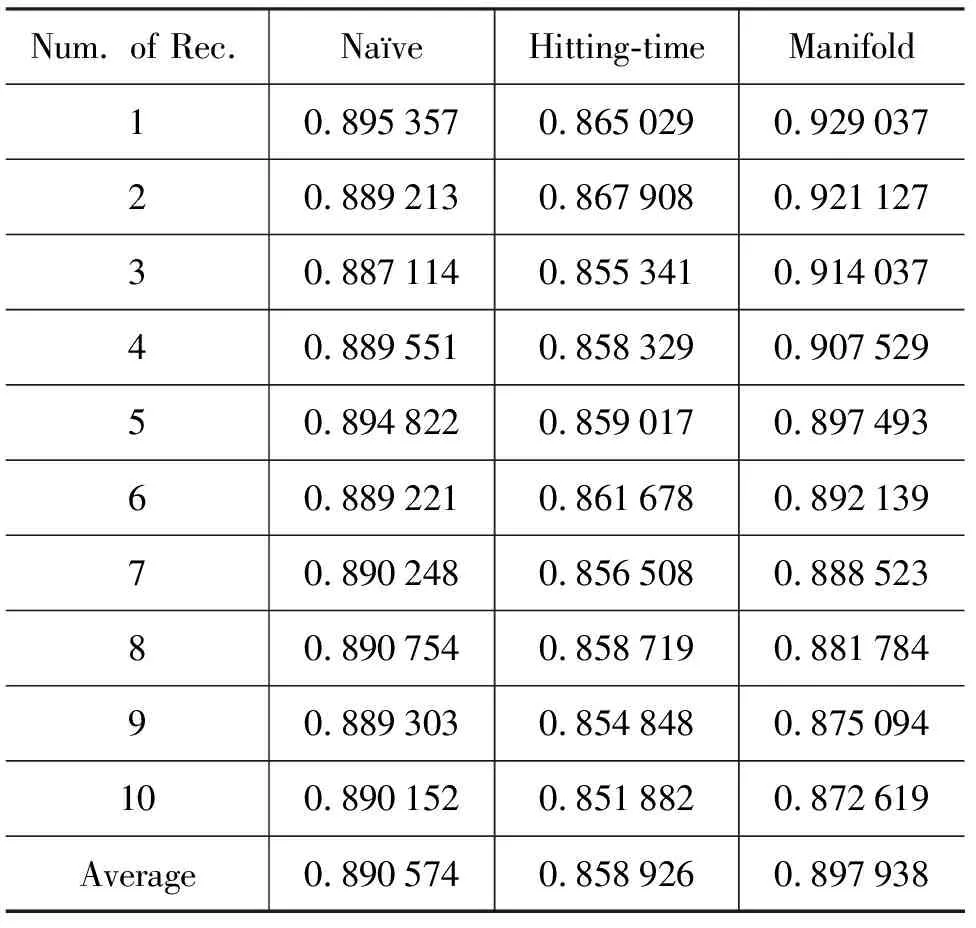
表2 三種查詢推薦方法(Na?ve Ranking, Hitting-timeRanking,Manifold Ranking)在不同推薦數目下相關性指標的比較

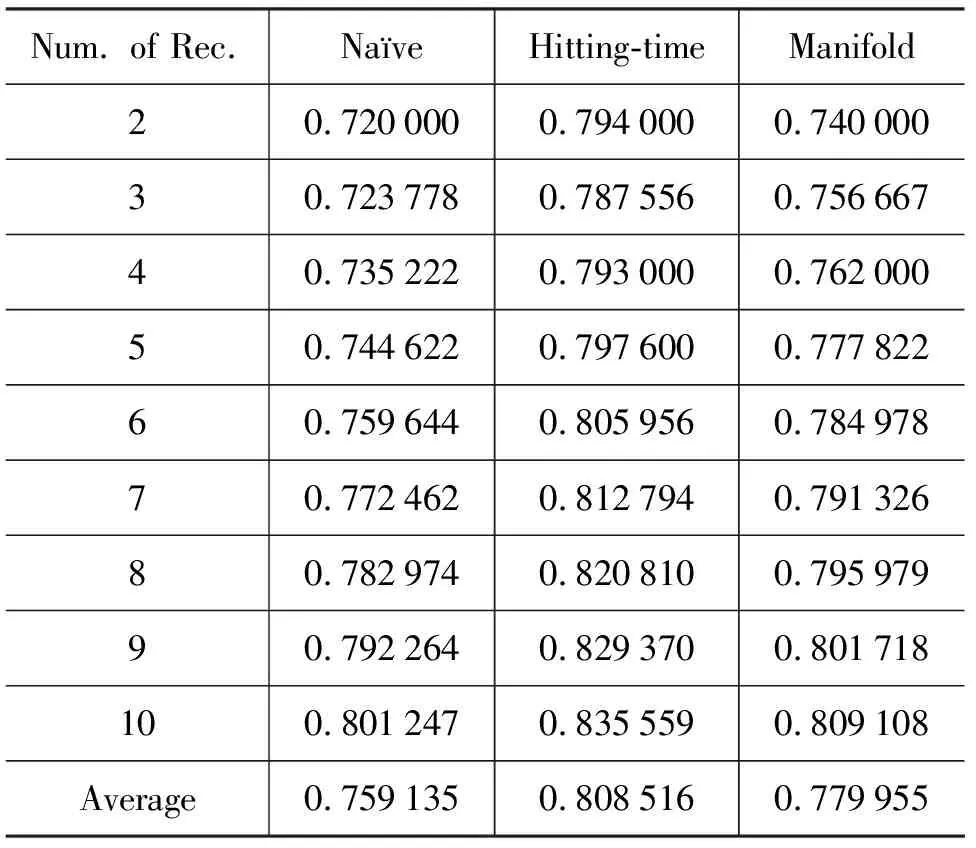
表3 三種查詢推薦方法(Na?ve Ranking, Hitting-timeRanking,Manifold Ranking)在不同推薦數目下差異性指標的比較

5 結論

本文中，我們提出了一種基于流形排序的查詢推薦方法，該方法通過利用查詢數據內在全局的流形結構來進行查詢推薦，避免了傳統查詢推薦方法在相關性度量方面和冗余性方面的不足。與現有Hitting-time Ranking相比，Manifold Ranking通過提升結構上具有代表性的查詢，從而使得所推薦的查詢與源查詢差異性得到的提高，同時保持較高的相關性。在一個大規模商業搜索引擎查詢日志上的實驗結果表明，Manifold Ranking要明顯優于兩種基準方法(Na?ve Ranking和Hitting-time Ranking)。

[1] H. Cui, J.-R. Wen, J.-Y. Nie, and et al. Probabilistic query expansion using query logs[C]//WWW ’02, 2002: 325-332.

[2] J.-R. Wen, J.-Y. Nie, and H.-J. Zhang. Clustering user queries of a search engine[C]//WWW ’01, 2001: 162-168.

[3] Q. Mei, D. Zhou, and K. Church. Query suggestion using hitting time[C]//CIKM ’08, 2008: 469-478.

[4] J. Surowiecki. The wisdom of crowds: why the many are smarter than the few and how collective wisdom shapes business[C]//Doubleday, Reading, MA, 2004.

[5] D. Beeferman and A. Berger. Agglomerative clustering of a search engine query log [C]//KDD ’00, 2000: 407-416.

[6] J.-R.Wen, J.-Y. Nie, and H.-J. Zhang. Clustering user queries of a search engine[C]//WWW ’01, 2001: 162-168.

[7] L. Li, Z. Yang, and et al. Query-url bipartite based approach to personalized query recommendation[C]//AAAI’08, 2008: 1189-1194.

[8] R. Baeza-Yates and A. Tiberi. Extracting semantic relations from query logs[C]//KDD ’07, 2007: 76-85.

[9] D. Zhou, O. Bousquet, T. N. Lal, and et al. Learning with local and global consistency[C]//NIPS’03, 2003.

[10] D. Zhou, J. Weston, A. Gretton, and et al. Ranking on data manifolds[C]//NIPS’03, 2003.

[11] J. He, M. Li, H.-J. Zhang, and et al. Manifold-ranking based image retrieval[C]//MULTIMEDIA’04, 2004: 9-16.

[12] X. Wan, J. Yang, and J. Xiao. Manifold-ranking based topic-focused multi-document summarization[C]//IJCAI’07, 2007: 2903-2908.

[13] E. Baykan, M. Henzinger, L. Marian, and I. Weber. Purely url-based topic classification[C]//WWW ’09, 2009: 1109-1110.

[14] P. Boldi, F. Bonchi, C. Castillo, and et al. Query suggestions using query-flow graphs[C]//WSCD ’09, 2009: 56-63.