矩陣變換器開關損耗分析與計算

涂方明 王亞楠

（1. 海裝駐武昌造船廠軍代室，武漢430060; 2. 中國船舶重工集團公司第七一二研究所，武漢 430064）

1 引言

矩陣變換器（Matrix Converter）作為一種通用變頻器具有人們所期望的多種優點，符合今后模塊化發展方向[1-3]。圖1為MC的基本結構，它主要由9個雙向開關組成。雙向開關的開關損耗分析是MC效率評估及系統設計的一個基本組成部分。由于MC的功率拓撲結構和調制策略與傳統的電壓源逆變器（VSI）大不相同，VSI的開關損耗分析不能適用于MC系統。對于MC系統，輸入電壓通過9個雙向開關整合調制直接連到輸出端，而不利用任何儲能元件，這樣便造成了IGBT模塊截止時Vce電壓不為恒值。即使輸出電流為恒值時，由于輸入電壓區間的切換，各個IGBT模塊的 c-e極電壓和電流分配都是在變化的，各管的損耗也同時在變化，因此對MC的損耗分析必須從調制策略和IGBT模塊的自身特性入手，研究各個開關模態下的開關損耗。國外對MC開關損耗的分析研究的較早，文獻[4]將MC和VSI的開關損耗進行了比較，其損耗模型不夠清晰，簡單的得到了兩個系統的仿真結果。文獻[5]將每個開關周期內的線電壓分為高、低兩類，對雙電壓調制下 MC開關損耗進行了分析和計算，得到了雙電壓調制下傳導損耗和開通、關斷損耗的估算解析表達式，但是其開通和關斷損耗的估算解析表達式并不能適用其它調制策略，影響了其通用性。

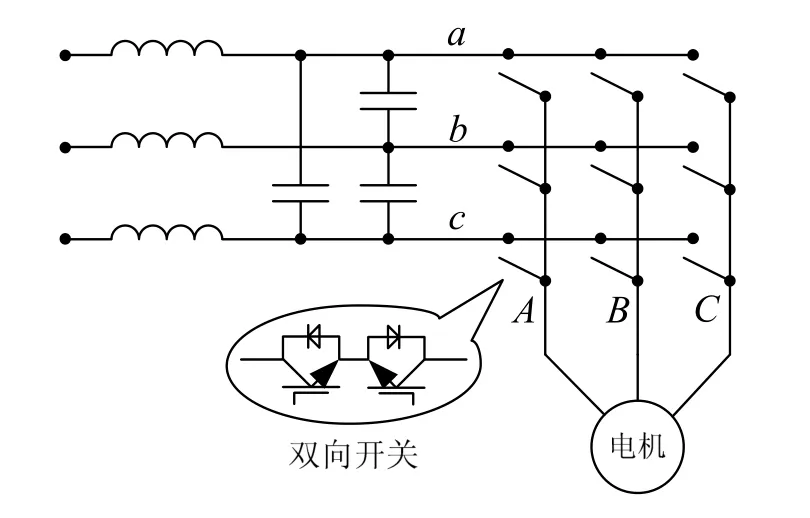
圖1 MC原理圖

本文針對上述文獻的不足，以電壓型換流法的各個開關模態為基礎，分析了各個模態的傳導損耗和各個模態之間轉換時的開通和關斷損耗，通過計算機累加仿真求得了MC總的開關損耗。由于調制策略對MC開通和關斷損耗影響較大，本文就幾種調制方法下的開關損耗進行了分析比較，得到了計算開通和關斷損耗的通用算法和估算表達式。

2 傳導損耗分析

2.1 IGBT的瞬時傳導損耗

IGBT導通時的物理特性決定了 IGBT的傳導損耗，其瞬時傳導損耗可以表示為通態壓降和通態電流的乘積，即：

其中 Vce為 IGBT集電極-發射極電壓，Ic為集電極電流。

而通常IGBT的伏安特性可由（2）式表示，其中Vceo為IGBT閾值電壓，Rk為通態等效電阻。

式（2）代入式（1）得：

2.2 電力二極管的瞬時傳導損耗

同樣，電力二極管的瞬時傳導損耗也可以表示為其通態壓降和通態電流的乘積，即：

其中VAK為通態壓降，Ic為通態電流。

而電力二極管的伏安特性可由（4）式表示，其中 VD0為二極管閾值電壓，RDk為通態等效電阻。

將式（4）代入式（3）得：

2.3 MC傳導損耗分析

因為MC的結構三相對稱，現只對其一相進行分析，由于MC的負載一般為感性，一個開關周期內負載可以作電流源處理，負載電流可以看作近似不變。根據 MC的調制策略不同，每個開關周期內的狀態變化順序也不盡相同，假設一個開關周期內某輸出相接入到輸入相有k個狀態，由圖2可知每個狀態總有也只有一個IGBT和一個二極管導通。

由于一個開關周期內開關切換的時間很短，次數也有限（只有k次），其間的傳導損耗相對整個開關周期傳導損耗很小，可以忽略，傳導損耗不受調制策略影響，所以一個開關周期內的傳導損耗應為IGBT和電力二極管傳導損耗之和：

圖3為 MC運行時的瞬時傳導損耗仿真波形，傳導損耗為與輸出頻率ωo有關的周期函數，由式（5）可求得MC單相平均傳導損耗為：

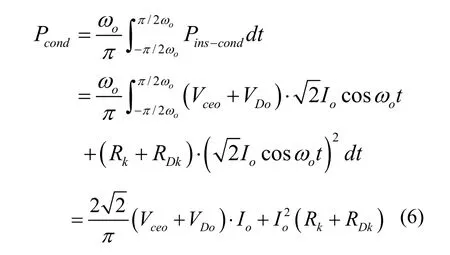
3 MC開通和關斷損耗分析

3.1 以輸入電壓區間劃分的各個開關模態

通常IGBT的開通和關斷損耗為其通態電流和斷態c-e極端電壓乘積的函數。硬開關模式下，單管單次開通損耗和關斷損耗分別為：

式中：Vce-on為開通前電壓，Ice-on為開通后電流。

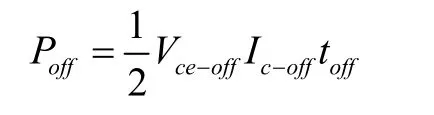
式中：Vce-off為關斷后電壓，Ic-off為關斷前電流。

圖2 MC單個開關周期內的狀態

圖3 MC瞬時傳導損耗仿真波形

由圖 2可知，輸入兩相之間進行換流時，IGBT的c-e極端電壓與輸入相有直接聯系，因此有必要按輸入電壓對各個開關模態進行劃分。以線電壓零點為界將輸入電壓周期劃分為 6個扇區，每個扇區中各相電壓的特點是一相為正極性，記為 VP，一相電壓為負極性，記為 VN，另一相為VM，可得VP＞VM＞VN。通過劃分，在每個扇區內可以將輸入ABC相映射為PMN相，并按照電壓高低排列，便于分析開通和關斷的過程，如表1所示（以Iout＞0為例）。

3.2 開通和關斷損耗模型

以輸出電流大于零，采用電壓型換流法由 P相換流到M相為例：P相導通時，SP1和DP2流過電流Iout，SM1預導通，DM2上承受VM—VP的反電壓，經過兩步換流法SP1硬關斷，SM2軟開通換流至M相，SM1流過電流Iout，SP1上承受VM—VP的電壓。其間只有 SP1產生關斷損耗如圖4所示，ton、toff為開通和關斷時間。同理可以分析 M 相到 N相、N相到P相等狀態的換流損耗，得到各狀態變換時的開通和關斷損耗如表2所示。

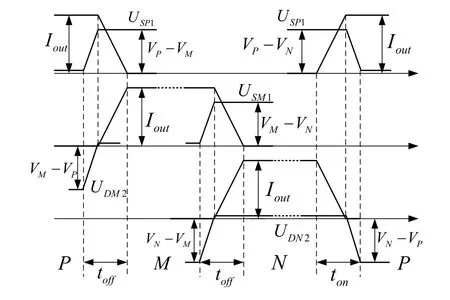
圖4 電壓型換流過程分析

3.3 Venturini法的開通和關斷損耗

利用表2得到的開通和關斷損耗模型可對整個MC進行仿真，圖5為采用Venturini法輸出頻率為 20Hz時瞬時開通損耗（黑影由損耗脈沖序列構成）。由圖可知，瞬時開通損耗受輸出電流頻率ωo的調制，但不是周期可積函數，不易得到像傳導損耗那樣的總損耗通用表達式。

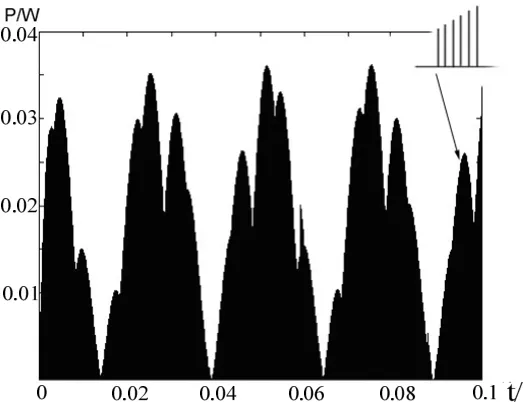
圖5 采用Venturini法，輸出頻率為20 Hz時瞬時開通損耗

觀察表2可知，各狀態變換時的開通和關斷損耗與輸入線電壓和輸出電流有關，為了便于分析，先只分析輸入線電壓對開通和關斷損耗的影響，再加入輸出電流的影響。圖6為采用Venturini法時各管的開通電壓波形，仿真結果顯示開通電壓不受輸出電壓及頻率的影響，圖6（a）中各管的開通電壓只受輸入線電壓的影響，為總共6個半波的脈沖序列，開通時總平均電壓為：

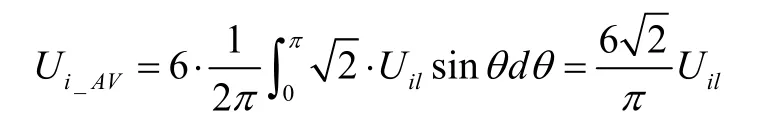
其中Uil為輸入線電壓有效值。

而輸出平均電流為：

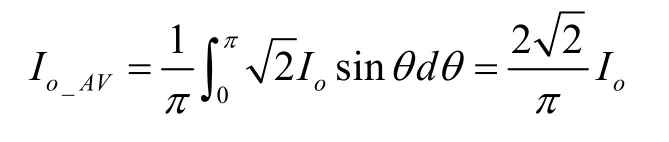
表1 以輸入電壓區間劃分的各個開關模態

表2 各模態換流開通和關斷損耗

其中IO為輸出電流有效值。

則單相輸出時的總開通損耗為：

其中fc為開關頻率。

各管開通損耗為：

若將普通Venturini法單個周期內的開關順序按圖6（b）進行優化，從仿真結果可以看出a、b兩相的開通損耗會減小50%，c相保持不變，總開通損耗是普通Venturini法的2/3。這是因為當A相輸出時，原來的開關順序是acbabc，現在變成aacbbc，a、b相的開通次數各減少了一次；當B或C相輸出時，a、b相的開通次數同樣會各減少一次。就單相輸出而言，各管的開通損耗由于調制策略的不同會呈現不平衡的現象。

這時開通時總平均電壓為：

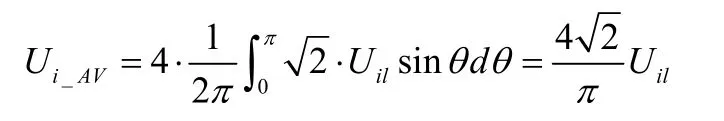
則單相輸出時的總開通損耗為：

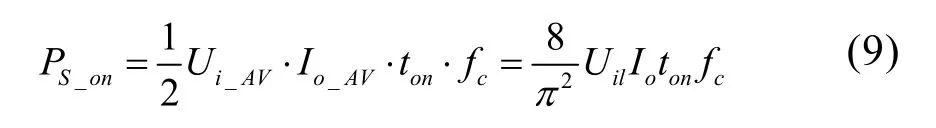
各管開通損耗為：

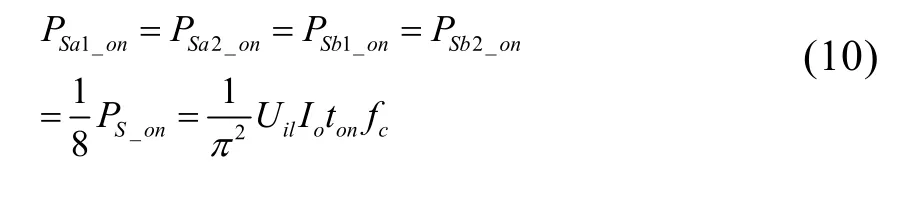
同理可以分析Venturini法的關斷損耗，結論類似，但上述方法并不能推廣到其它一般情況，例如空間矢量調制法，圖7為采用空間矢量調制法，輸出頻率為20 Hz時的開通電壓波形，其中各管的開通電壓不僅受輸入線電壓的影響，而且還受輸出頻率的影響，波形近乎不規則，這與空間矢量法的調制方法有關。和Venturini法的每個開關周期都是固定順序的旋轉矢量不同的是，空間矢量法是通過輸入電流和輸出電壓區間的組合有選擇的挑選靜止矢量，區間的不同導致了開通電壓選擇輸入線電壓的不同，所以空間矢量調制法很難得到開通時的總平均電壓解析表達式，單管也是，只能通過仿真得到近似的數值解。

圖6 采用Venturini法時各管的開通電壓波形

表3為四種調制方法下的開通損耗系數，其中優化空間矢量法通過調整普通空間矢量法每個開關周期內的矢量順序使得每次換流只開關一次。從表3可以看出，與Venturini法開通損耗系數不隨輸出頻率變化不同，空間矢量法的開通損耗系數隨輸出頻率增加而略有增長，但是同條件下，空間矢量調制法的開通損耗還是明顯小于Venturini法（Venturini法的每個開關周期有6次狀態，空間矢量法采用對稱調制有9次）。

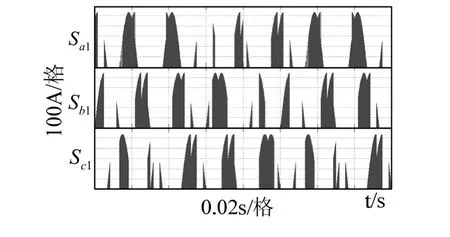
圖7 采用空間矢量調制法，輸出頻率為20 Hz時的開通電壓波形

由此，并不是所有的調制方法都能得到開通和關斷損耗的解析表達式，調制方法的不同，總體、各管的開通和關斷損耗也大不相同，只有在特殊的情況下（如Venturini法）才能得到精確的解析解，大多數調制方法的開通和關斷損耗必須針對其調制過程進行仿真累加計算。

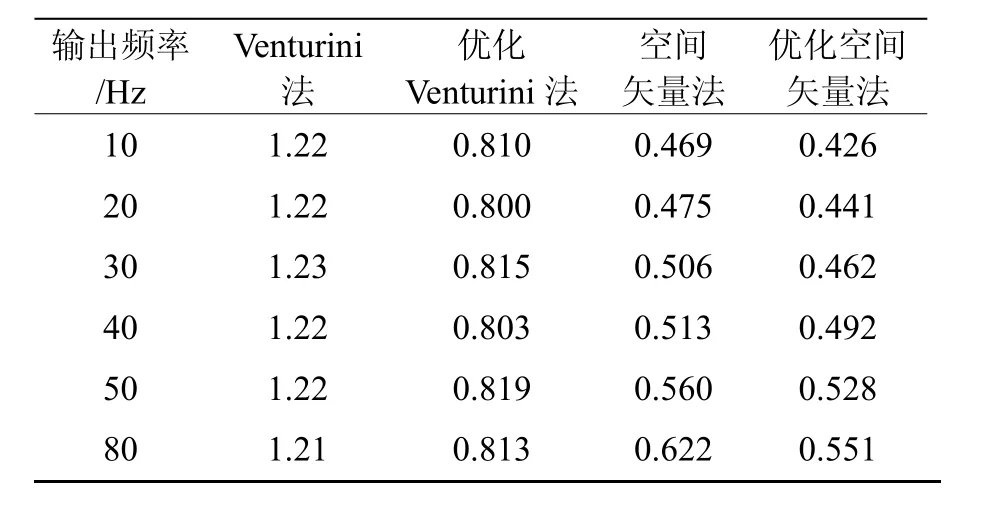
表3 四種調制方法的開通損耗系數（10 kHz）

圖8為不同開關頻率、不同調制方法下開關損耗，可以看出開關頻率和調制方法對傳導損耗沒有什么影響，而對開通和關斷損耗很大。比較四種調制方法，優化空間矢量法的總體開關損耗最小，Venturini法最大。

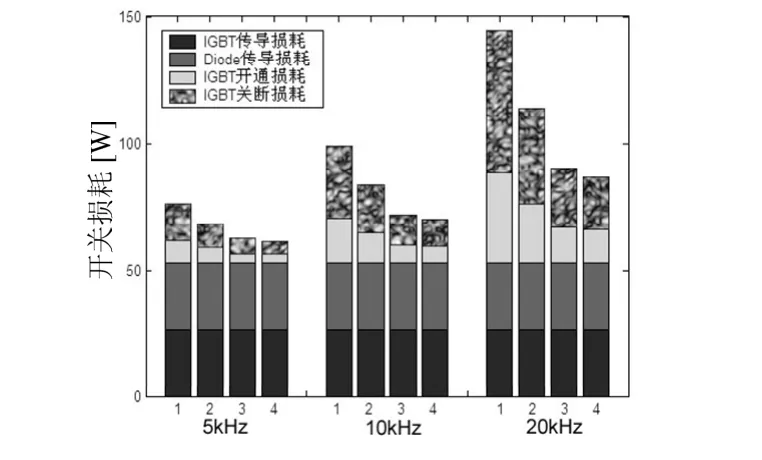
圖8 開關頻率對損耗的影響

4 結論

本文通過計算機累加仿真的方法對矩陣變換器的開關損耗進行了分析和計算，就幾種調制方法下的開關損耗進行了分析比較，給出了計算傳導損耗、開通和關斷損耗的具體通用算法。仿真可知傳導損耗為與輸出頻率ωo有關的周期函數；不同的調制方法、開關頻率對開通和關斷損耗的影響很大，對傳導損耗幾乎沒有影響。

目前，雙向開關由 IGBT和快速恢復二極管以共集電極或共發射極組合構成，隨著大功率MOS、IGBT技術的日臻成熟，新型的開關器件將會被采用，現在已經開始出現RB-IGBT器件和整合模塊技術應用于 MC，相信不久的將來會成為主流采用的雙向開關，本文所闡述的開關損耗方法雖然是基于IGBT模塊反串聯的結構，但是其分析方法仍可以推廣到其它器件模型。

[1]Wheeler P W, Rodriguez J, Clare J. Matrix converters：a technology review[J]. IEEE Trans. on Industrial Electronics, 2002, 49(2)：276-288.

[2]Blaabjerg F, Casadei D, Klumpner C. Comparison of two current modulation strategies for matrix converters under unbalanced input voltage conditions[J]. IEEE Trans. on Industrial Electronics,2002, 49(2)： 289-296.

[3]Lars Helle, Kim B Larsen, Blaabjerg F. Evaluation of modulation schemes for three-phase to three-phase matrix converters[J]. IEEE Trans. on Industry Electronics, 2004, 51(1)：158-171.

[4]Apap M, Clare J C, Wheeler P W. Comparison of losses in matrix converters and voltage source inverters[C]. IEE Seminar on Matrix Converters, 2003,4： 1-6.

[5]Kang Jun-Koo, Hara H, Yamamoto E. Analysis and evaluation of bi-directional power switch losses for matrix converter drive[C]. 7th IAS Annual Meeting,2002, 1：438-443.