圓錐截交線上特殊點的求法
田福潤, 陳 光, 劉玉潔
(長春工程學院機電學院,吉林長春 130012)
1 截交線上各特殊點的位置
平面與圓錐相交,截交線是平面與圓錐表面的共有線[1-3]。根據截交線是平面上的線這一性質,我們把平面和截交線單獨畫出。分析一下截交線上各特殊點在平面上的位置。一平面和平面上一條曲線(橢圓)的兩個投影如圖1所示。
平面ABCD可認為是一個截平面,橢圓可認為是截平面ABCD與圓錐的截交線。從圖1水平投影分析,橢圓上的最前點Ⅰ和最后點Ⅱ,一定是平面上與橢圓相切的兩條正平線與橢圓的兩個切點。同樣道理,橢圓的最左點Ⅲ和最右點Ⅳ,一定是平面上與橢圓相切的兩條側平線與橢圓的兩個切點。橢圓的最高點Ⅴ和最低點Ⅵ,一定是平面上與橢圓相切的兩條水平線與橢圓的兩個切點。

圖1 特殊點的位置
由以上分析可知,橢圓上的最前、最后、最左、最右、最高、最低等特殊點,都是平面上與橢圓相切的各投影面平行線與橢圓的切點。根據這一特性,則可以通過作圖求出這些特殊點。
2 確定截交線上各特殊點作圖方法
2.1 輔助切平面法
特殊點作圖方法如圖2所示。
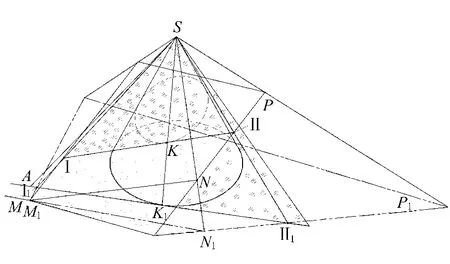
圖2 特殊點作圖方法
從圖中可見,圓錐被平面P所截切,截交線為一橢圓。我們先分析橢圓上最前點(或最后點)的確定方法。
橢圓上的最前點K一定在平面P與橢圓相切的正平線上[4]。如果平行與平面P上的正平線作一個與圓錐相切的平面,如圖中平面SAB,則有:
1)圓錐的切平面SAB與平面P相交,交線為一條正平線ⅠⅡ。
2)圓錐的切平面SAB與圓錐相切為一條素線SK1。
3)由于ⅠⅡ,SK1都是SAB平面上的直線,所以ⅠⅡ與SK1有唯一的一個交點K。
根據上述結果可推理出:
1)點K即在平面P上(在ⅠⅡ上),又在圓錐表面上(在SK1上),所以K點是平面P與圓錐表面的共有點,即截交線上的點。
2)由于ⅠⅡ線是圓錐切平面SAB上一條直線,所以ⅠⅡ線與圓錐表面相切,切點即是K點。
3)由于ⅠⅡ線又是平面P上一條正平線,它與圓錐表面的切點K,即為平面P上的一條正平線與截交線的切點,也就是截交線上的最前點。
通過以上論證,可以得出求解截交線上的最前點(或最后點)的作圖方法:平行于平面P上的一條正平線MN作圓錐面的切平面SAB(可作兩個),求出切平面SAB與圓錐面的切線SK1,切線SK1與平面P的交點K就是截交線上的最前點(或最后點)。
對于最左、最右、最高、最低點的確定方法[5-6],與最前、最后點的方法基本相同,不同之處只是切平面的位置不同,方法如下:
1)確定最左、最右點,是平行與平面P上側平線作圓錐面的相切平面。
2)確定最高、最低點,是平行與平面P上水平線作圓錐面的相切平面。
2.2 輔助投影法
確定截交線上的各特殊點,除了輔助切平面法外,還可以采用輔助投影的方法[7](見圖2)。要確定截交線上最前點K,可以用中心投影的方法,即以錐頂S為投影中心,把錐面和平面P向錐底面所在平面進行投影。投影結果使錐面的投影都聚在錐底面的曲線上,平面P的投影成為P1(雙點劃線表示),平面P上與截交線相切的正平線ⅠⅡ投影成Ⅰ1Ⅱ1,Ⅰ1Ⅱ1與錐底面曲線相切K1點,K1點即是截交線的最前點K的中心投影。K1確定之后,返回投影即可以確定出K點,具體作圖方法如下:
1)以錐頂S為投影中心,把錐面投影到錐底面上,投影積聚成錐底曲線。
2)以錐頂S為投影中心,把平面P上的任意一條正平線MN投影到錐底面所在平面,投影成M1N1。
3)根據兩條平行直線的中心投影交于同一滅點的特性,求出M1N1的滅點F(圖中未畫出),然后過F點作錐底面曲線的切線,此切線就是平面P上與截交線相切的正平線ⅠⅡ的中心投影Ⅰ1Ⅱ1,切點K1就是線與截交線的切點K的中心投影。
4)把K1反投影回去,即連接K1S,求出K1S與平面P的交點K,K點就是截交線的最前點。
上面是用輔助投影的方法確定截交線上最前點(或最后點)的作圖方法。最左、最右、最高、最低等各點的確定方法基本相同。不同之處只是把平面P上的不同投影面平行線進行中心投影。
3 作圖舉例
求平面P與斜橢圓錐的截交線,如圖3所示。
1)用變換投影面X1使平面P積聚成P1。
2)求特殊點。
①求最前點、最后點(輔助切面法):
a.過錐頂S平行與平面P的正面跡線PV作斜橢圓錐的兩個切面SAB,方法如下:
過錐頂S作一條平行PV的直線SA,求出SA的水平跡點a。
過a作錐底面曲線的切線ab(兩條),則SAB就是平行PV直線,并與錐面相切的平面(兩個)。
b.求出切平面SAB與斜橢圓錐的切線SB,SB的水平投影為sb(兩條)。
c.利用變換投影面X1,求出sb與平面P的交點1,2,這兩點即是截交線上的最前點和最后點的水平投影。
②求最左點、最右點[8](輔助投影法):
a.采用中心投影法,把平面P上的任意一條側平線MN投影到水平面上得M0N0。
b.連接M0N0,求出其滅點F。
c.過滅點F作斜橢圓錐底面的切線Fd(兩條),d為切點。
d.連接Sd,利用變換投影面X1,求出Sd與平面P的交點3,4,這兩點即是截交線上的最左點和最右點的水平投影。
③求最高點、最低點:
利用變換投影面X1,可直接求出截交線上的最高點和最低點的水平投影5,6。
3)連線。
把以上各點連接起來,就可以準確作出截交線的投影形狀。圖中截交線的正面投影未畫。
4 結 語
文中只討論了圓錐截交線特殊點的求法,其它曲面體截交線特殊點的求法還有待探討。
[1] 張華鈾.截交線和相貫線的控制要點:求特殊點[J].機械研究與應用,2005(5):37-45.
[2] 劉朝儒,彭福蔭,高政一.機械制圖[M].北京:高等教育出版社,2001.
[3] 大連理工大學工程畫教研室.機械制圖[M].北京:高等教育出版社,1999.
[4] 彭志廣,鮑衛芳.求相貫線特殊點問題一例的探討[J].中國民航學院學報,2000(4):95-98.
[5] 李冰,薛頌菊.圓柱與圓錐相貫時相貫線上特殊點的討論[J].北京建筑工程學院學報,2001(4):213-220.
[6] 龍子勇,劉雯.相貫線上兩個特殊點投影的求法[J].太原科技,2002(2):45-47.
[7] 蘇步青,華宣積.空間解析幾何[M].上海:上海科技出版社,1984.
[8] 劉鐵祿.準確求解圓錐、圓柱正交相貫最右點[J].東華大學學報,2006(5):77-85.

