模糊遞歸神經網絡在軟測量中的應用

彭曉波

（湖南工業大學 電氣與信息工程學院，株洲 412007）

0 引言

在現代工業過程中，對控制的要求越來越高。因而要達到較高的控制精度，必須對測量的各種過程變量也有很高的要求，一般解決工業過程測量精度不斷提高的方法是研制新型的過程檢測儀表，以滿足生產過程中對質量和產量進行控制的要求。但是這類過程變量大都具有難測的特點，而且研制新型檢測儀表成本非常高、研制周期長，測量對象、范圍和功能都受到一定的限制；因此，有必要尋求一種新的思路。近年來在過程控制和檢測領域涌現出的軟測量技術正是這一思想的集中體現。

軟測量建立待測變量與可測或易測過程變量之間的非線性函數關系，間接得到待測變量的估計值。經過多年的發展，已經形成了一些較為成熟的軟測量建模方法：機理建模[1]；基于人工神經網絡建模[2]；模糊建模[3]；集成建模[4]。機理模型是通過對機理過程中物質和能量的轉化過程進行分析,得到機理數學表達式，每個系數均具有實際物理意義。但實際模型的結構是非常復雜，由于對生產過程的認識是不全面的，就導致了其檢測精度就會隨著生產過程的不同階段，不同條件的變化而變化，從而無法建立較好的機理模型。神經網絡是目前軟測量研究中最活躍的領域，它是根據對象的輸入輸出數據直接建模，在解決高度非線性和嚴重不確定性系統控制方面具有巨大的潛力，特別適用于工業過程的軟測量建模。但是，一般神經網絡是一種靜態映射，不適合用來表示動態映射[5,6]。而一般的生產過程都是動態的，因此動態遞歸神經網絡對于動態過程的軟測量，提供了一種極具潛力的選擇，代表了神經網絡軟測量的發展方向。模糊理論模擬人類思維，是處理模型未知或具不確定性的復雜系統的一種有效手段。近年來，模糊理論與神經網絡結合構成模糊神經網絡大量應用于軟測量中，它既有模糊邏輯表達定性知識的能力，又有神經網絡很強的自學習和處理定量數據的能力，因而非常適合處理一些復雜的非線性軟測量建模問題。

本文結合遞歸神經網絡和T-S模糊模型，提出了基于T-S動態遞歸型模糊神經網絡的軟測量模型，不僅可以很好地反映動態的生產過程，還具有定性知識表達的能力，把它應用在冶煉過程，獲得了很好的效果。

1 T-S動態遞歸型模糊神經網絡(DTRFNN) 的結構

如圖1所示，本文提出了DTRFNN結構。

DTRFNN被分為6層，形式如下：

Rule r：IFχ1(t) is Ar1andχ2(t) is Ar2and hr(t) is G Then y (t+1) =αr0+αr1+χ1(t) + …αrN+1h1(t)and… h1(t+1) isr1and… hr(t+1) isrr

這里描述DTRFNN：

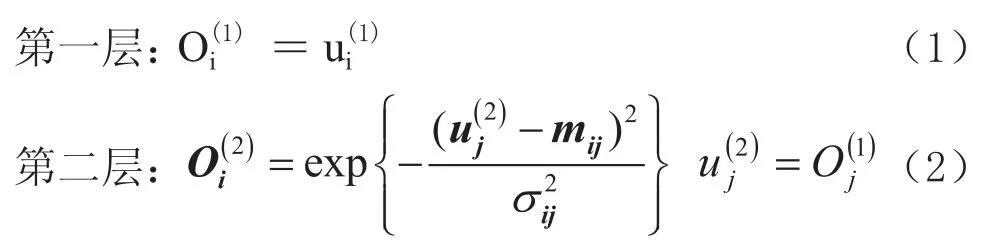
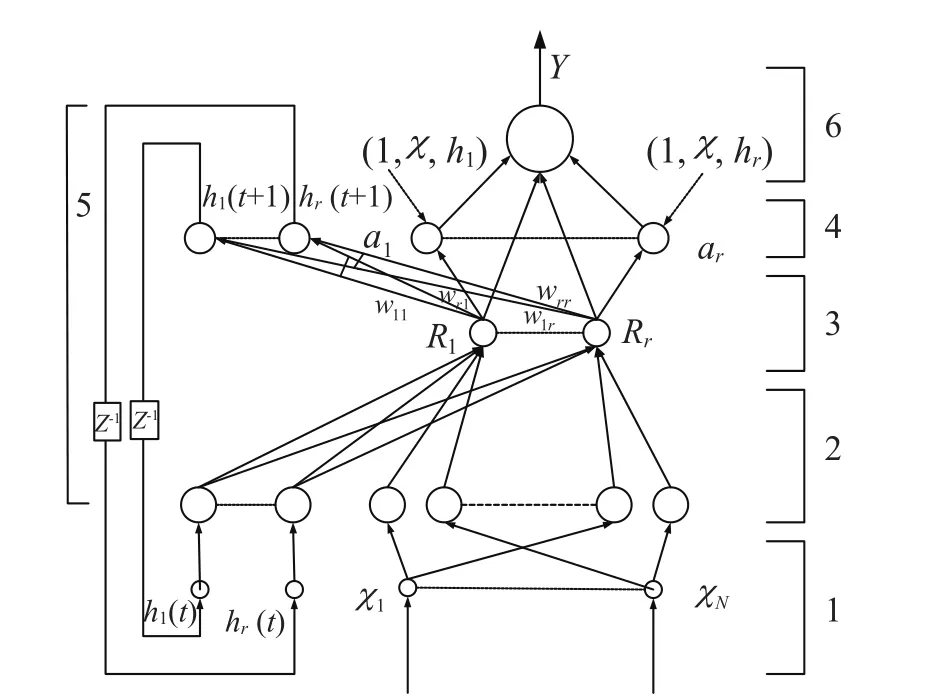
圖1 DTRFNN 的結構

2 T-S動態遞歸模糊神經網絡在工業過程軟測量中的應用

冶煉過程和化工過程是非常復雜的動態工業過程，在反應過程中伴有強烈的氧化和還原反應、物相的變化及能量的轉換。從控制的角度看,冶煉過程屬于典型的非線性過程，是大滯后、強耦合、分布式的連續動態過程。現在的冶煉廠和化工廠控制系統一般采用DCS系統，采用前饋-反饋方式進行在線控制。在反饋控制中，某些金屬的含量，金屬化合物的溫度、微量金屬比等等工藝參數是重要的反饋信息，這些參數的穩定對生產的穩定至關重要。但是目前這些參數很多都是通過人工獲得，測量值在時間和準確性上都嚴重影響了控制系統的效果，如果采用測量傳感器，因為工藝原因，經常要更換，成本非常高，這樣急需一套實用的軟測量方法來滿足生產的需要。因此，目前的參數測量方式很難保證生產過程長期穩定，導致了產量和質量很難有本質上提高，而且單位產量的能耗一直居高不下。針對工藝參數測量這個關鍵問題。本文采用了T-S遞歸模糊神經網絡軟測量模型，以解決以上的測量問題。

在某冶煉過程中，渣中金屬的流失不可避免，但是如果有合適的鐵硅比，可以大大的減少金屬的流失，并且金屬溶劑和渣的分層也是由鐵硅比決定的，因此對鐵硅比的測量直接影響到了金屬的產量，但是鐵硅比的測量都是由通過人工現場取樣，然后再到化驗室進行化驗，這樣會導致這些參數比實際參數要滯后很多，而且認為主觀的因素占了很大一部分，因此測量值在時間上和準確性上都嚴重影響了控制系統的效果，本文采用T-S動態遞歸模糊神經網絡對鐵硅比進行軟測量

對于這個軟測量模型, 輸入變量的選擇是非常重要的。通常可以檢測的間接變量有幾十個，將這些檢測變量都作為輸入變量顯然是不符合要求，而且也容易造成計算量的過大。因此輸入變量的選擇可根據工藝與實際經驗來確定[7]，也可采用相關分析法[8]， 確定與被軟測量變量最相關的幾個間接輸入變量。表一 給出了某冶煉過程中軟測量模型的輸入輸出變量。

質量指標鐵硅比作為控制目標量，即DTRFNN輸出參數；氧、風、溶劑、精礦、煙灰、精礦成分11個量為操作參數，即DTRFNN的11個輸入參數。

首先，根據現場采集到的大量數據(包括輸入變量和輸出變量) 對DTRFNN 進行學習。需要指出的是，在對輸入、輸出數據要進行預處理，因為數據隨時可能出現“異常點”，還有數據歸一化的問題，最重要是要考慮輸出變量與輸入變量的滯后問題。即t 時刻的數據(可以是化驗分析值) 是與（T-S）時刻的輸入數據對應的，根據工藝操作經驗，S一般為60min。經過大量的數據仿真分析，最后確定DTRFNN 的結構為11-55-5-5-1，即輸入變量為6個 ，第二層的節點數是55個，第三層和第四層的節點數都是5，輸出變量為1個,即鐵硅比。

對鐵硅比給出了仿真結果，對幾個月的生產數據進行處理、進行訓練，50多組數據進行驗證。在圖2中，DTRFNN的結果用星號來表示，實際值用圓圈來表示。從數據中，我們可以知道DTRFNN平均準確率達到了很高。顯示了DTRFNN能很好的對冶煉參數進行軟測量。進行推廣，DTRFNN也可以對復雜的大型工業過程參數進行軟測量，為解決過程工業參數測量的難題提出了一條新的思路。

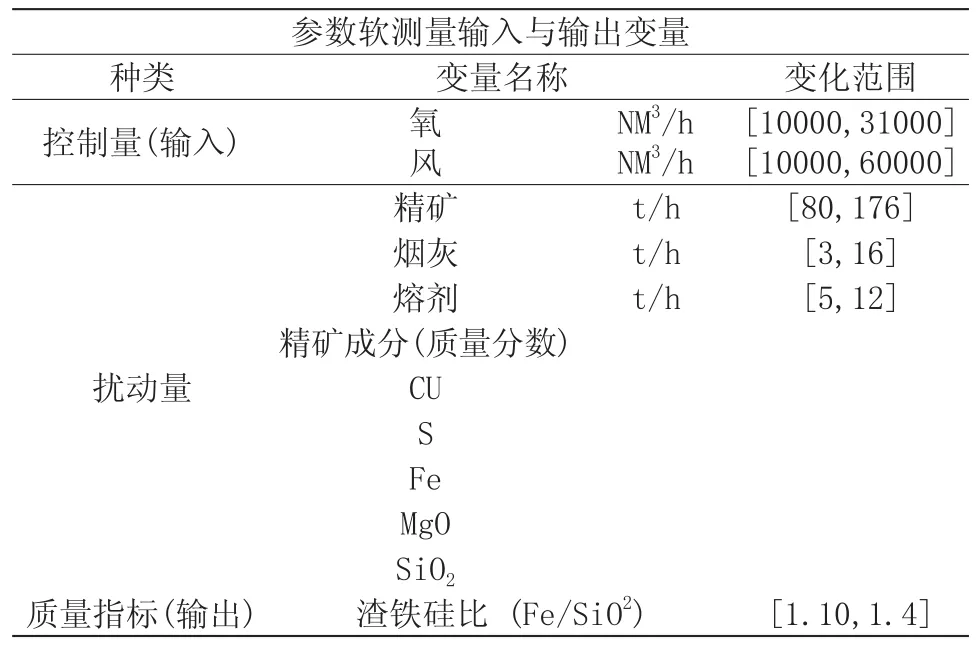
表1 參數軟測量輸入與輸出變量

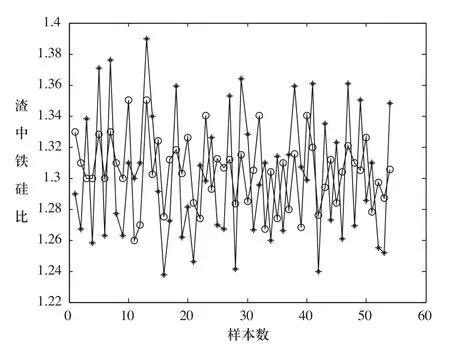
圖2 渣中鐵硅比的DTRFNN輸出與實際值

3 結論

針對參數測量在過程工業中的問題，本文采用了DTRFNN動態軟測量模型，對它的結構進行了描述。并結合在冶煉過程中金屬元素含量的測量，結果表明，DTRFNN動態模型能很好的實現軟測量，取得了良好的效果。

[1] 楊慧中.聚丙烯腈質量指標軟測量模型的數據動態校核[J].華東理工大學學報, 2001, 27(5):536-639.

[2] 李勇剛,桂衛華,陳峰.基于因素分析的復合神經網絡及其在軟測量中的應用[J].信息與控制,2004,33(2):141-144.

[3] 馬銘, 孟慶鍇, 張利彪.基于模糊系統優化的軟測量建模[J].遼寧工程技術大學學報, 2010, 29(5):763-766.

[4] 陳曉方, 桂衛華, 王雅琳, 吳敏, 陽春華.基于智能集成策略的燒結塊殘硫軟測量模型[J].控制理論與應用, 2004,21(1): 75-80.

[5] C H Lin, W D Chou, F J Lin.Adaptive recurrent neural control for nonlinear syetem tracking.IEEE Proc.Control Theory Appl, 2001,148(2): 156-168.

[6] Tommy W S, Chow, Yong Fang.A recurrent neuralnetwork-based real-time learing control strategy applying to nonlinear systems with unknown dynamics.IEEE Trans.Indust.eLEC, 1998, 45(1):153-161.

[7] 于靜江, 周春暉.過程控制中的軟測量技術[J].控制理論與應用, 1996, 13 (2): 137-144.

[8] 宋德臻.軟測量技術及其在工業過程中的應用[D].杭州:浙江大學, 1998.