模糊PID控制光電跟蹤系統的抗干擾性分析

徐曉霞

（西安工業大學 北方信息工程學院 電子信息系，陜西 西安710025）

抗干擾性和穩定性是控制系統的一項重要指標，同時也是系統能夠正常工作的首要條件。因此，分析系統的抗干擾性和穩定性并給出保證系統穩定的措施，是設計一個良好控制系統的首要前提。與經典控制理論相比，模糊控制系統的穩定性理論還不夠完善，這是因為模糊控制系統本質上是一種復雜的非線性系統，對其穩定性的分析目前還很難給出統一的分析工具，而且模糊控制系統的表現形式也各不相同，同樣為理論分析增加了巨大的難度。文中針對模糊自適應PID控制的機載光電跟蹤系統，通過引入模型參數攝動和增加外界干擾的方法研究系統的穩定性和抗干擾性能，最終得到系統穩定的結論，為今后模糊自適應控制器的設計提供了理論依據。

1 機載光電跟蹤系統的數學模型

機載光電穩定跟蹤系統是一個典型的機電隨動系統，其數學模型如圖1所示。

圖中θg為飛行員給定的或視頻圖像跟蹤器給定的目標瞄準線指令角；K2/（T1s+1）為視頻圖像信號的慣性環節；K1s為復合控制器；C1為跟蹤回路的控制器；Kp/[s（τ2s+1）]為陀螺回路的傳遞函數；C2為穩定回路的控制器；Ka，Ke，Km分別為力矩電機的電流常數，反電勢系數和力矩系數；Ra為電樞電阻；τ3為機電時間常數；J∑為負載轉動慣量；θ為穩定平臺轉角，并且θ反饋用旋轉變壓器或微動同步器實現；M±是由載機運動、機身振動、摩擦等引起的干擾力矩的總和，這種干擾力矩對不同的轉軸是不同的，并且是非線性函數。圖1中復合控制環節K1s的作用是為了提高系統的無靜差度而設計的。

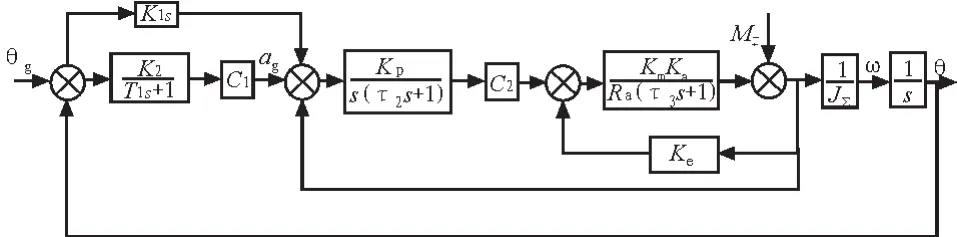
圖1 穩定跟蹤系統的數學模型Fig.1 Mathematical model of a stable tracking system

為了建立正確可靠的數學仿真模型，首先要對控制對象進行參數辨識，我們用時域分析法或頻域分析法可以得到粗跟蹤系統包括電流環、速度環在內的對象傳遞函數為[3]：

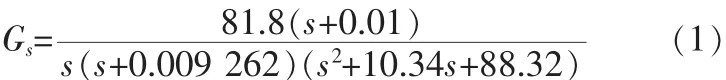
機載光電跟蹤系統中存在著較大的延遲環節、功放飽和、電機死區以及陀螺漂移等，再加上對系統的跟蹤精度要求又非常高，所以對于這樣一個系統，研究它的穩定性和抗干擾性非常重要。針對模糊自適應PID控制的機載光電跟蹤系統，通過引入模型參數攝動和增加外界干擾的方法研究系統的穩定性和抗干擾性能，最終得到了系統穩定的結論，為模糊自適應控制器的設計提供了理論依據。

2 分析模糊控制機載光電跟蹤系統的穩定性

相平面法是 Poincare在 1885年首先提出來的，其實質是將系統的運動過程形象地轉化為相平面（狀態平面）上一個點的移動，通過研究點移動的軌跡，就能獲得系統運動的全部信息[6]。由于相平面法只能用來研究一階或二階非線性，筆者所研究的機載光電跟蹤系統通過將速度回路等效簡化后，可以認為是一個二階控制系統，因此可以用相平面法進行穩定性分析。

應用相平面法分析非線性系統的前提是繪制系統的相軌跡。可以通過解析法、圖解法或實驗的方法做出。為了更直觀地體現系統結構和仿真結果，這里采用SIMULINK可視化動態仿真的方法進行分析。實驗仿真圖如圖2所示。

中設計的機載光電跟蹤伺服系統的速度環的閉環傳遞函數為：

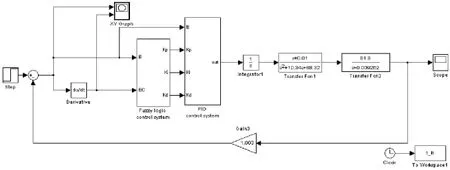
圖2 系統模型實驗仿真框圖Fig.2 System block diagram based on experimental simulation model

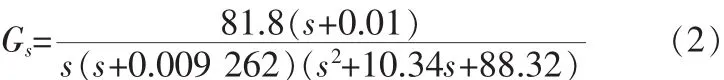
當系統輸入為階躍函數時，模糊控制機載光電跟蹤系統的相軌跡如圖3所示。

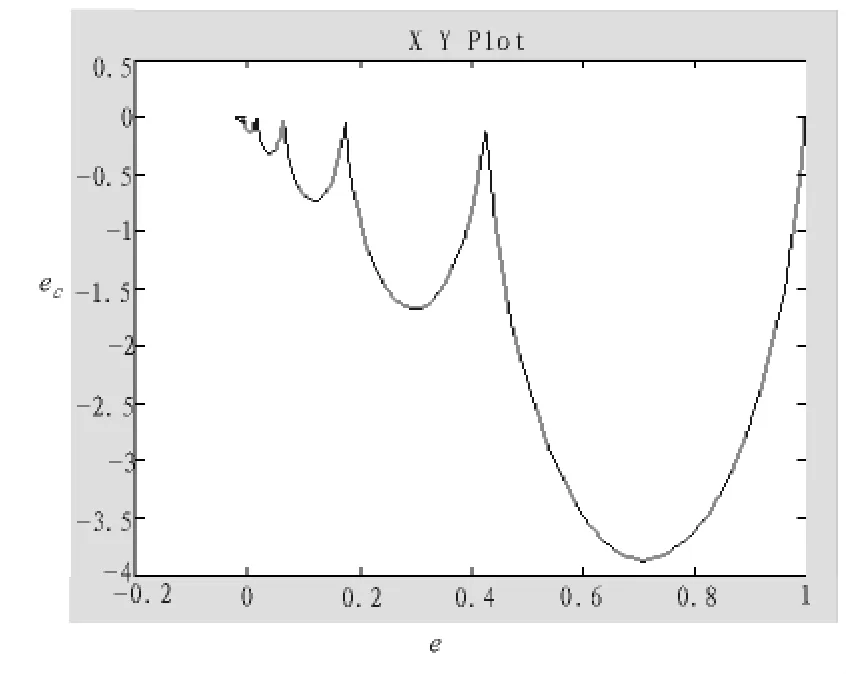
圖3 機載光電跟蹤伺服系統階躍輸入下的相軌跡曲線Fig.3 Phase trajectory curve of Airborne electro-optical tracking servo system under the step input

由圖中曲線可以看出，系統可以很快達到平衡點，無極限環現象發生，其相軌跡收斂于相平面的原點，故系統是穩定的。模糊控制系統穩定性的分析目前還處于發展階段，雖然在理論上已取得了大量研究成果，但是在針對實際控制系統還是沒有統一的方法，文中基于工程可實現的基礎上，用相平面法對所設計的模糊控制系統進行了穩定性分析，這種方法簡單易行，可操作性強，具有較好的實際意義。

3 模糊控制機載光電跟蹤系統的抗干擾性分析

機載光電跟蹤系統是一個復雜的非線性系統，影響其性能品質的因素很多。文中建立的數學模型是略去很多非線性因素建立的線性模型，是沒有外界干擾下的模型，和實際系統有一定的區別，為說明模糊自適應PID控制對不確定性系統有較強的魯棒性，下面引入模型參數攝動方法，即增加外界干擾的方法進行仿真。

1）模型攝動1

從下面 6 幅圖中可以看出，1、2、3、-1、-2、-3 弧度調轉模糊PID控制時，系統能夠較快跟蹤給定輸入，且都在1.3 s時間內系統達到穩定。而采用PID控制和模糊控制時，系統嚴重震蕩，一段時間后還是無法穩定。

2）模型攝動2

從上面 6 幅圖中同樣可以看出，1、2、3、-1、-2、-3 弧度調轉模糊PID控制時，系統能夠較快跟蹤給定輸入，且在1.3 s時間內系統達到穩定。而采用PID控制和模糊控制時，系統嚴重震蕩，一段時間后還是無法穩定。

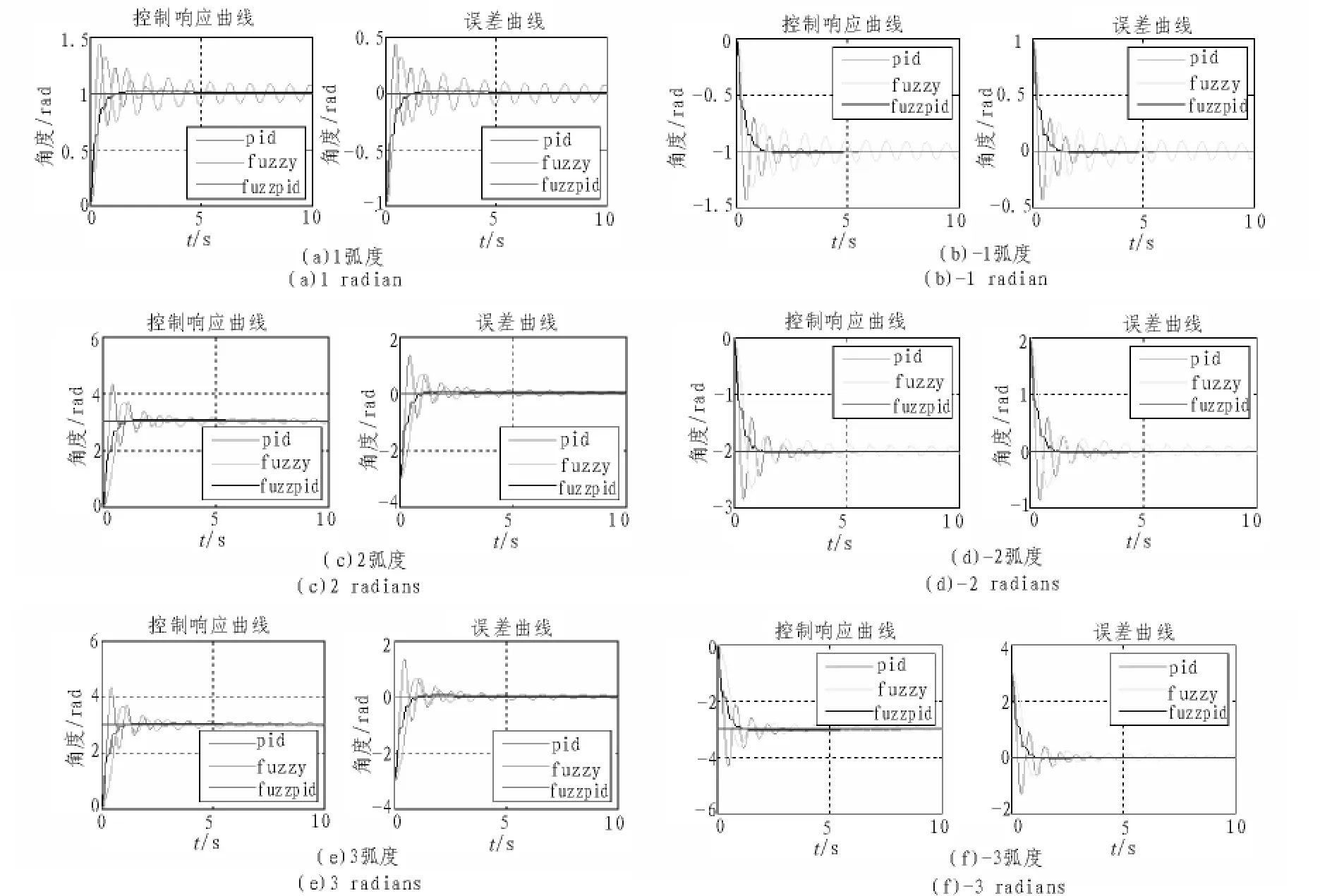
圖4 模型攝動1下不同弧度調轉控制響應曲線和誤差曲線Fig.4 Response curve and error curve under model perturbation 1 of different curvature turned control

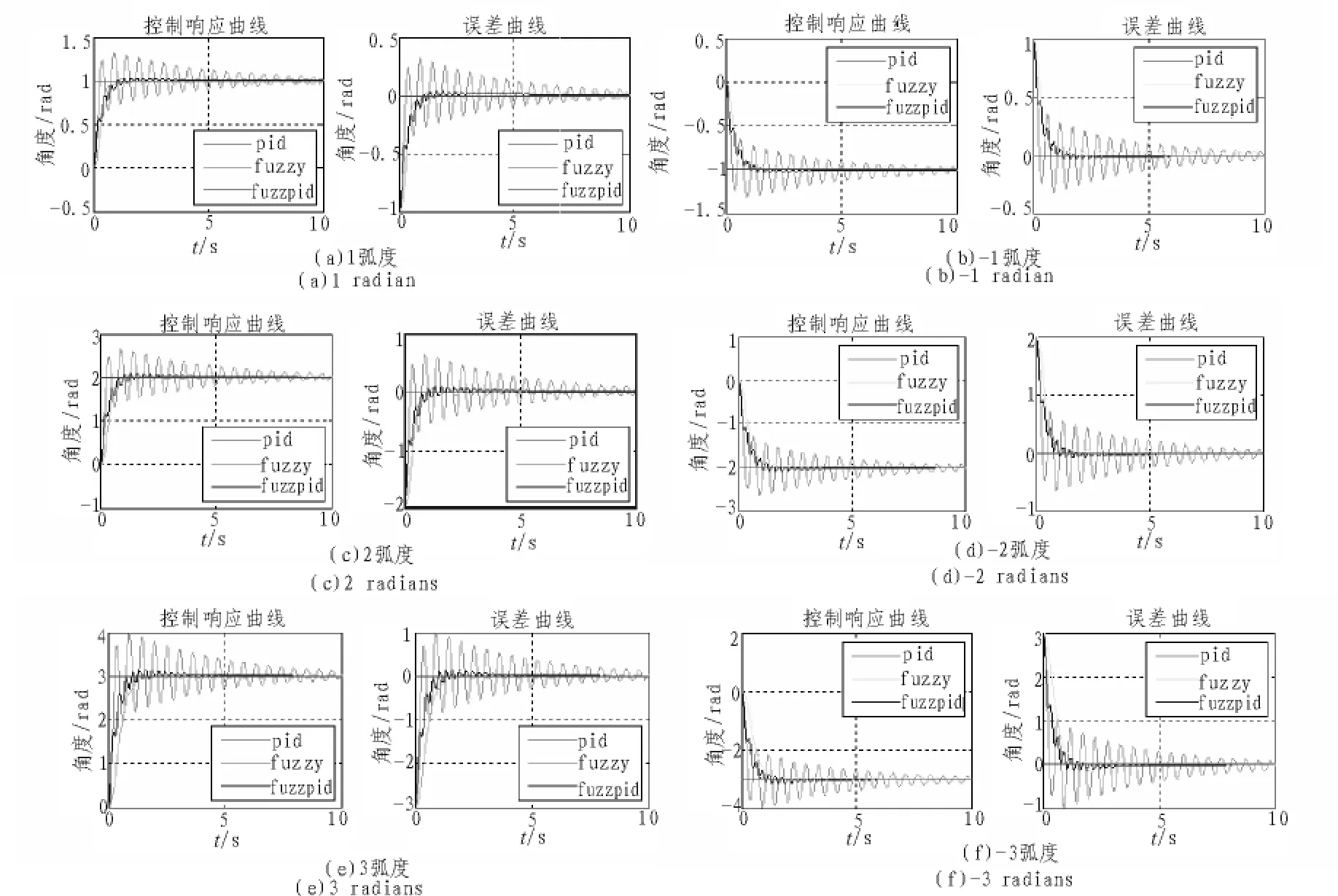
圖5 模型攝動2下不同弧度調轉控制響應曲線和誤差曲線Fig.5 Response curve and error curve under model perturbation 2 of different curvature turned control

3）外干擾

干擾源：控制輸出疊加零均值均方差為0.1的高斯白噪聲。

從上面 6 幅圖中可以看出，1、2、3、-1、-2、-3 弧度調轉模糊PID控制時，系統能夠較快跟蹤給定輸入，且在1.3 s時間內系統達到穩定。而采用PID控制和模糊控制時，系統嚴重震蕩，一段時間后還是無法穩定。

上述計算機仿果實驗結果表明，在滿足機載光電系統性能指標的要求下，運用模糊PID控制理論設計的控制器能夠在充分考慮模型不確定定性和外界干擾不確定的情況下，有效地保證機載光電跟蹤系統的控制精度。

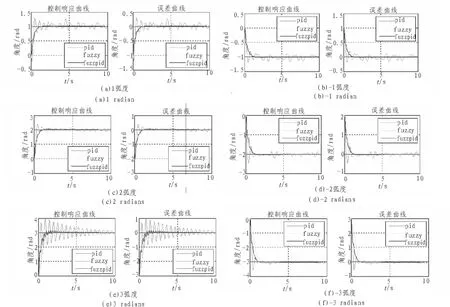
圖6 外干擾下不同弧度調轉控制響應曲線和誤差曲線Fig.6 Response curve and error curve under outside interference of different curvature turned control

4 結 論

文中主要介紹模糊控制光電跟蹤系統的穩定性和抗干擾性。首先建立了機載光電跟蹤系統的數學模型，然后利用相平面法分析模糊控制機載光電跟蹤系統的穩定性，接著通過引入模型參數攝動和增加外界干擾的方法研究了系統的抗干擾性能，最終得到了系統穩定的結論，為模糊自適應控制器的設計提供了理論依據。

[1]袁莉芳，胡佑德.采用多模控制技術在直流伺服系統[J].北京理工大學學報，2007，17（3）：337-339.

YUAN Li-fang，HU You-de.DC servo system using multicontrol technology [J]. Journalf Beijing Institute of Techonology，2007，17（3）：337-339.

[2]侯宏錄，周德云，王偉，等.模糊PID控制在光電跟蹤中的應用[J].光電工程，2006，33（5）：12-16.

HOU Hong-lu，ZHOU De-yun，WANG Wei，et al.Application of fuzzy-PID control in system of Photo-electric tracking[J].Opto-Electronic Engineering， 2006，33（5）：12-16.

[3]王嬋娟，王強.單神經元模糊PID控制在光電跟蹤系統中的應用[J].光電工程，2006，33（2）：33-34.

WANG Chan-juan，WANG Qiang.Single neuron fuzzy PID control application in photoelectric tracking system[J].Opto-Electronic Engineering，2006，33（2）：33-34.

[4]薛定宇，張曉華.控制系統計算機輔助設計MATLAB語言與應用[M].北京：清華大學出版社，2006.

[5]盧廣山.高精度機載光電跟蹤系統的自適應算法研究[J].西北工業大學學報，2002，20（4）：564-566.

LU Guang-shan.Adaptive fuzzy control of AEOTS（Airborne Electro-Optical Tracking System）[J].Journal of Northwestern Polytechnical University，2002，20（4）：564-566.

[6]PEI Xin-dong， WANG Qin-ruo， YU Tao.The application of fuzzy PID control in aerosol automatic confecting system[J].Proceedings of the 4th World Congress on Intelligent Control and Automation， 2002（2）：923-926.