SSCA算法改進及性能分析

鄭 鵬 ， 張 鑫 ， 劉 鋒 ，， 陶 然

（1.海軍航空工程學院 電子信息工程系，山東 煙臺 264001；2.北京理工大學 信息科學技術學院，北京 100081）

譜相關理論由Gardner W A等人深入研究并發展[1-2]，其優點主要表現在分辨率高、抗干擾能力強、雙頻率域信息豐富且易于提取等。在通信、雷達、遙測、水聲、電子對抗等領域中，由于某些人為的或無意的調制，而使大量信號呈現出循環平穩性，因此譜相關理論在信號檢測、參數估計、系統辨識、調制識別、故障診斷等現代信號處理諸多領域中得到了越來越深入的研究。循環譜估計是譜相關理論的主要研究對象，對循環譜的估計是研究循環平穩過程的重要前提，也是其應用基礎，循環譜估計方法中工程應用最廣的主要是基于FFT的時域平滑法中的FAM和SSCA、頻域平滑法中的FSM[3-4]。其中SSCA算法因其計算量最小，計算效率最高，因此在工程中得到了廣泛應用，其采用方法[5]都是文獻[3-4]中提到的經典算法，但是這種算法存在循環譜泄露的問題，而且會產生錯誤的循環特征[6-7]，其循環譜估計效果并不理想，本文在已有文獻基礎上提出了一種改進的SSCA算法，該算法能夠改善譜估計，便于實現檢測、參數估計、調制識別等后續信號處理。

1 循環譜基本理論

設x（t）為循環平穩信號，其均值和自相關函數呈現以T0為周期的周期性，即

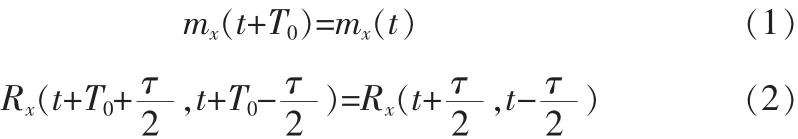
那么可以將（2）式展開成Fourier級數的形式，即

其中α為循環頻率，循環自相關函數Rαx（τ）是Fourier級數的系數，

Rαx（τ）的 Fourier變換 Sαx（ f）稱為循環譜密度，簡稱循環譜：

由上述分析可以看出，Rαx（τ）可以看成 x（t）的兩個復數頻移分量 u（t）和 v（t）的互相關

由式（5）可以看出，Sαx（f）=Sαuv（f）。由互譜分析可以得到

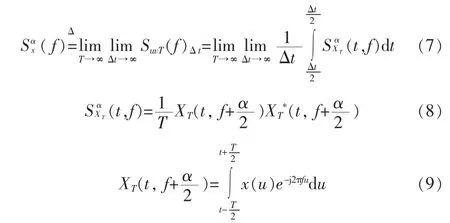
其中，式（7）是循環譜密度估計式，式（8）是循環周期圖，式（9）是接收數據的短時傅里葉變換。Δt是接收數據的長度，T是短時傅里葉變換的窗長，上式*表示復共軛。

循環周期圖不能直接作為譜相關函數的估計值，它的方差很大，而且隨著采集時間的增大并不趨為零，同時，它也不是無偏估計。為了減小估值誤差，減小譜泄露，得到循環譜可靠估計，對于有限時間長度的接收數據，必須對循環周期圖進行平滑處理。平滑分為時域平滑和頻域平滑兩種，其中時域平滑因具有較高的計算效率和較小的計算量而在工程中被廣泛采用。在這里采用時域平滑的循環周期圖來估計信號的循環譜密度。循環譜密度估計的時域平滑SSCA算法可以表示為

其中 XT（r，f）是復解調，又被稱為循環周期圖，a（n）為數據衰減窗，gc（n）為平滑窗，q=-P/2，…，P/2-1，L 為抽取因子，滿足L＜N′，當L=N′/4時效果最好。N為總的采樣數，LP=N。SSCA算法的實現原理圖如圖1所示。

圖1 SSCA算法實現Fig.1 Realization of SSCA

SSCA算法的頻率分辨率為Δf=fs/N′，循環頻率分辨率為Δα=1/Δt=fs/N。要得到循環譜可靠估計，使循環譜密度函數的估計與時間幾乎不相關，需滿足可靠性條件：

由上式可見要實現可靠估計，循環頻率分辨率Δα必須比頻率分辨率Δf高得多。

（1）從產業轉移角度分析，建筑業、工業與交通運輸、倉儲和郵政業在區域間的轉移趨勢明顯。東北、華北和華東地區表現為相對穩定的轉出，而中南、西南和西北地區表現為穩定的轉入，產業結構的空間調整同時也對能源強度的空間分布產生影響。

2 算法改進及數字實現

算法改進之處在于線性內插和數據加窗：

1）復解調實現的內插方法 由于信道化處理的采樣處理，復解調的采樣速率為fs/L。在SSCA算法的實現過程中要求復解調與未進行濾波處理的原始信號共軛進行相乘，而原始信號的采樣速率fs。為了完成乘法運算需要對復解調進行內插處理以使其采樣速率與原始信號共軛相匹配。傳統方法采用的是“保持”的處理方法，即將每一個復解調復制L次，但是這種方法會產生錯誤的循環特征。因此，本文采取了線性內插方法來代替“保持”的方法。

2）數據加窗 算法的第2個改進之處在于窗函數的選擇。對窗函數的選擇應滿足以下要求：a（n）應具有大的衰減，gc（n）應具有小的帶寬。在Gardner的經典文獻中提到兩者分別采用漢明窗和矩形窗，這種方法被廣泛采用。實際上這種選擇并不十分合適，對循環譜泄露和虛假循環特征的產生的抑制效果并不是很好。基于窗函數的選擇要求，本文采取了適應性更強的凱澤窗，通過調整窗函數的參數來達到最好別的效果。

改進算法的實現原理圖如圖2所示，數字實現過程如下：

圖2 改進的SSCA算法實現Fig.2 Realization of innovatory SSCA

1）n時刻N′的點數據加窗，然后進行N′點FFT；

2）折疊運算。求出一個周期的頻譜，得到信號的復解調表達式，即 fk=k（fs/N′），k=-N′/2，…，N′/2-1；

3）求出 n 時刻復解調的相關，即 XT（n， fk）x*n，得到 N′個數據；

4）采用線性內插對采樣后的復解調進行賦值，重復1，2，3直到 n=N，得到 N×N′矩陣；

5）對N×N′矩陣中的每一列求N點FFT，得到頻率和循環頻率分別為

的N個數據。

通過上面步驟，可以看出SSCA算法主要有3個階段：

第1階段：利用N′點FFT計算數據的復解調。

第2階段：計算復解調與信號的共軛相關。

第3階段：計算N點FFT，得到循環譜估計值。

需要指出的是SSCA算法由于利用原始信號代替復解調信號的復共軛，采用了1個復解調濾波器，它的輸出信噪比相對于FAM算法有所減小，但換來了較小的計算量。

3 仿真實驗及結果分析

若噪聲為加性平穩噪聲，那么MPSK信號的模型表示為：

其中：xl（t）為 x（t）的復包絡；f0為信號載頻；θk為調制相位信息，θk∈{2π（k-1）/M}，k=1，…，M；q（t）為成型脈沖；Tc為碼元寬度，其倒數fc為碼元速率。

MPSK信號循環譜的一般形式[8-9]如下，當M=2時，即BPSK信號的循環譜為：其中

可以看出，對所有MPSK信號，在α=n/Tc處均取得較大非零值，而在其它地方取值為零或接近于零。BPSK信號的循環譜除具有上述特征外，在f=0，α=2f0n/Tc處也取得較大非零值。本文采用BPSK、QPSK信號作為仿真對象，噪聲為高斯白噪聲。仿真中參數設置如下：采樣頻率fs=8 192 Hz，載頻f0=2 048 Hz，碼片速率為fc=512 Hz，信號初始時間和初始相位均為0。

圖3是算法改進前后BPSK信號循環譜密度。圖4是取f=0其中切面循環譜包絡。圖5是算法改進前后QPSK信號的循環譜密度。圖6是取f=fc其中切面的循環譜包絡。由圖可以看出算法改進前信號的循環譜在錯誤的循環頻率處出現了峰值，循環譜泄露現象仍舊比較明顯，而改進算法則對上述兩種現象抑制效果明顯，這對于信號循環特征的提取時十分有利的，這說明改進算法對循環譜估計效果要好于原算法。

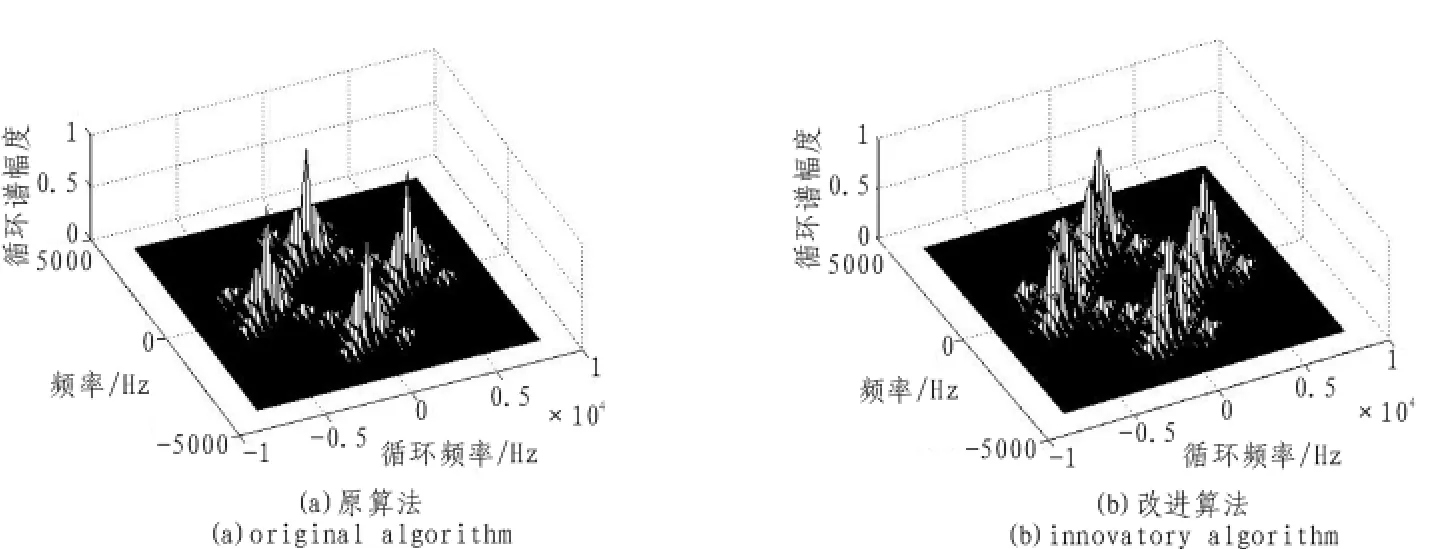
圖3 BPSK信號的循環譜密度Fig.3 Cyclic spectrum of BPSK signal

圖4 BPSK信號f=0處循環譜包絡Fig.4 The amplitude of BPSK signal’s cyclic spectrum

4 結 論

隨著對信號處理研究的深入，譜相關理論的應用會越來越廣。本文針對SSCA算法存在譜泄露以及產生錯誤的循環頻率信息等問題，提出了一種改進算法，這種算法實現簡單，能夠有效地改善循環譜估計，這對于信號檢測、參數估計、調制識別等后續信號處理是十分有益的。

[1]Gardner W A.Statistical spectral analysis：a non-probabilistic theory[M].NJ：Prentice-Hall， Englewood Cliffs，1988.

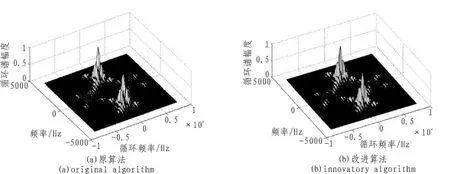
圖5 Cyclic spectrum of QPSK signal Fig.5 QPSK信號的循環譜密度

圖6 QPSK信號f=0處循環譜包絡Fig.6 The amplitude of QPSK signal’s cyclic spectrum

[2]Gardner W A.Exploitation of spectral redundancy in cyclostationary signals[J].IEEE SP MAG，1991，（04）：14-36.

[3]Roberts R S，Brown W A，Loomis H H， et al.Computionally efficient algorithms for cyclic spectral analysis[J].IEEE Signal Processing， 1991，8（2）：38-49.

[4]Brown W A，Loomis H，Jr.Digital implementations of spectral correlation analyzers[J].IEEE Trans.Signal Processing，1993，4（2）： 703-720.

[5]高玉龍，張中兆.SSCA算法改進及實現[J].哈爾濱工業大學學報，2008，40（9）：1374-1377.

GAO Yu-long，ZHANG Zhong-zhao.Modification and realization ofSSCA algorithm[J].JournalofHarbin Institute of Technology，2008，40（9）：374-1377.

[6]Gillman A M.Non co-operative detection of LPI/LPD signals via cyclic spectral analysis[D].ADA 361720/XAB，1999.

[7]Eric April.On the implementation of the strip spectral correlation algorithm forcyclic spectrum estimation[M].Ottawa：Defence Research Establishment，1995.