泥沙參數選擇方法及在懸沙濃度研究中的應用
董 佳,張寧川
(大連理工大學海岸和近海工程國家重點實驗室,大連116024)
目前,在港口和海岸工程工可研階段,論證工程對泥沙運動及海床演變影響多采用數值模擬方法[1-3]。該方法中需要確定諸多影響泥沙運移的基本參數,如泥沙沉降速度、泥沙擴散系數、控制侵蝕速度的比例值、軟底床的侵蝕系數、硬底床的侵蝕指數、床面糙率、河床淤積物的干密度、床層間的泥沙轉換率等。上述參數選擇恰當與否將直接影響數值計算的可靠性。通常情況,研究者通過實測資料驗證或經驗獲取得,然而當實測資料缺乏或經驗不足時,往往難以得到符合實際的計算結果。
對于泥沙沉降速度可通過物理模型試驗或較為成熟的經驗公式計算得到較為可靠的數值;對于以潮流為主要環境動力的淤泥質海床而言,經過數值計算表明,泥沙擴散系數,控制侵蝕速度的比例值,軟底床的侵蝕系數,硬底床的侵蝕指數等對懸沙濃度的影響較小。因而以潮流為主要動力的淤泥質海域懸沙濃度計算中,床面糙率、河床淤積物的干密度、床層間的泥沙轉換率3個參數的最佳取值需要進行詳細探討。
首先建立二維水動力模型,在通過實測資料驗證的基礎上,進行懸沙濃度計算,定量地討論了每個參數的選擇對懸沙濃度的影響程度。在床面糙率、河床淤積物的干密度、床層間的泥沙轉換率可變范圍內,分別調整各個參數的取值,以計算得到的懸沙濃度變化與實測資料吻合為目標,搜尋得到上述3個參數的最優取值。在此基礎上,對洋山港全水域中各特征點的懸沙濃度進行了模擬并和實測值吻合較好,驗證了所選擇參數的可靠性。
1 水流泥沙數學模型
1.1 控制方程
水流泥沙數學模型控制方程包括潮流控制方程和懸沙濃度控制方程。
對于潮流控制方程,采用包含二階紊動項的平面二維非恒定流體運動方程
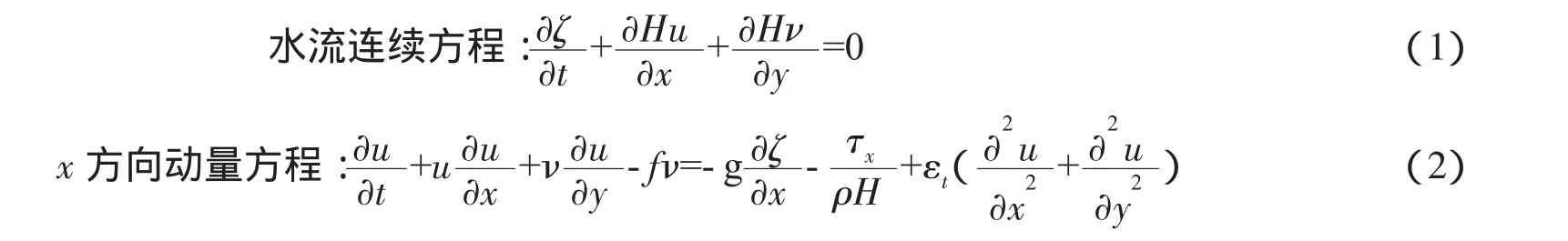

式中:S為懸沙濃度;Sm為泥沙的沉降和再懸浮濃度;Cb為底層泥沙濃度;τb為瞬時床底剪切應力;τcd為淤積臨界剪切應力;τce為侵蝕臨界剪切應力;ε為泥沙水平擴散系數;α為軟底床的侵蝕系數;n為硬底床的侵蝕指數;E為控制侵蝕速度的比例因子。
1.2 定解條件
(1)初始條件:在計算的初始時刻給出潮位、懸沙濃度等初始值,其選取范圍較為寬松,因為初始條件的誤差可以在正確的邊界條件控制下很快消失。
(2)潮流模型開邊界條件:在海域開邊界,海面水位的邊界條件由邊界處主要分潮的調和常數計算可得

式中:Em為該點相對于平均海平面的水位;ai、wi、φi分別是第i格分潮的振幅、頻率和遲角。
(3)潮流模型固體側邊界條件:在研究區域的固體側邊界處,一般假定垂直于固體海岸的法向速度為零,即。
(4)懸沙濃度計算模型開邊界條件:在入流時段S為給定值,在出流時段由下式計算得

(5)懸沙濃度計算模型固體邊界條件:一般假定固邊界處,法向泥沙通量為零,即。
1.3 數值計算方法與網格生成方法
數值計算采用中心有限體積法。考慮到非結構網格具有節點隨意編號、網格隨意加密以提高精度、可以對復雜的固岸邊界和水下地形進行比較精確的模擬、少量的節點數可得到滿意的精度等優點,故在數值計算中網格采用非結構網格。
1.4 水動力模型驗證
以洋山港工程水域為水動力模型驗證對象。洋山深水港位于上海市南匯嘴東南海域的崎嶇列島海域,該工程近十幾年積累了豐富且可靠性較高水動力、泥沙現場同步觀測資料。模型范圍為東經121.8°~122.3°,北緯30.3°~30.8°,該范圍計算網格共剖分為35 394個。
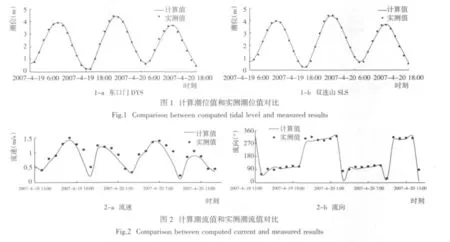
水動力模型驗證包括計算水域潮位、流速及流向驗證等內容。圖1給出了潮位計算值與實測值的比較示例,圖1結果表明,不同位置潮位實測值和計算值吻合良好。圖2給出了流速、流向計算值與實測值的比較示例,圖2結果表明,不同位置流速及流向的實測值和計算值的吻合程度很高。模擬計算結果較好地再現了洋山港區非正規半日潮、水流流動往復性較強的特點。
2 泥沙參數取值及對懸沙濃度的影響
2.1 懸沙濃度計算的主要影響參數篩選
如前所述,影響泥沙運動的參數包括泥沙沉降速度、泥沙擴散系數、控制侵蝕速度的比例值、軟底床的侵蝕系數、硬底床的侵蝕指數、床面糙率、河床淤積物的干密度、床層間的泥沙轉換率。
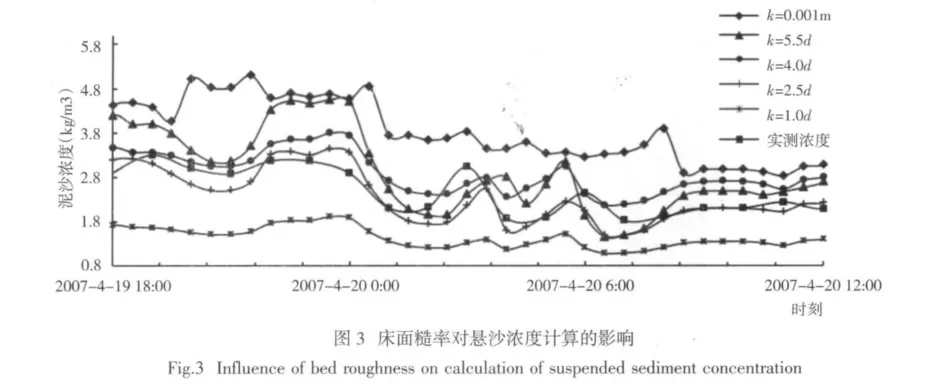
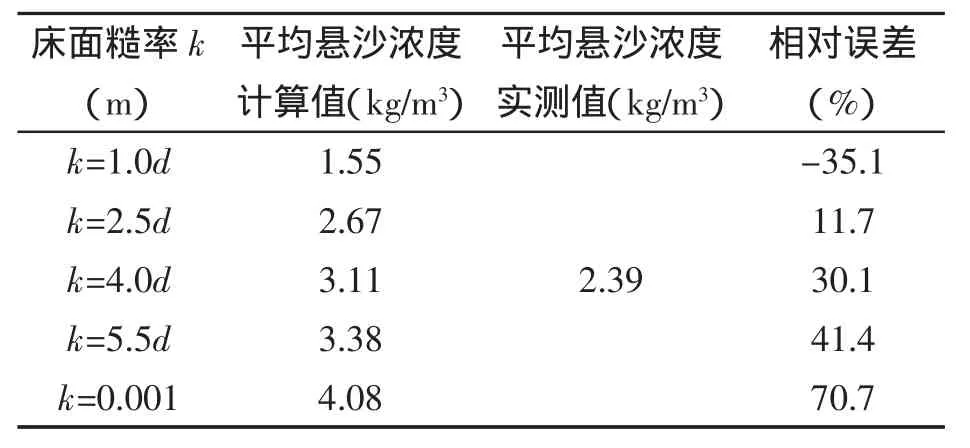
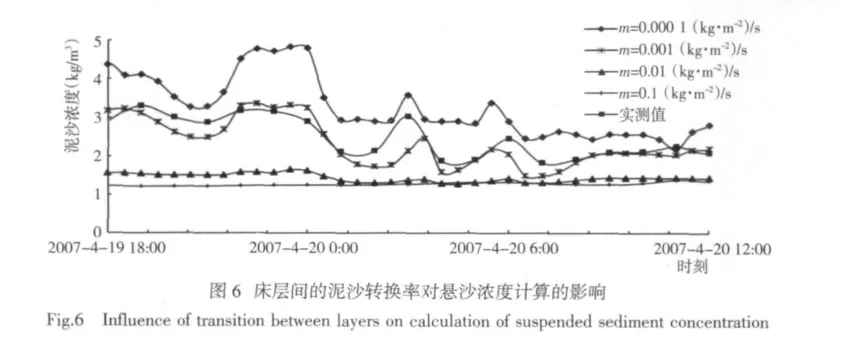
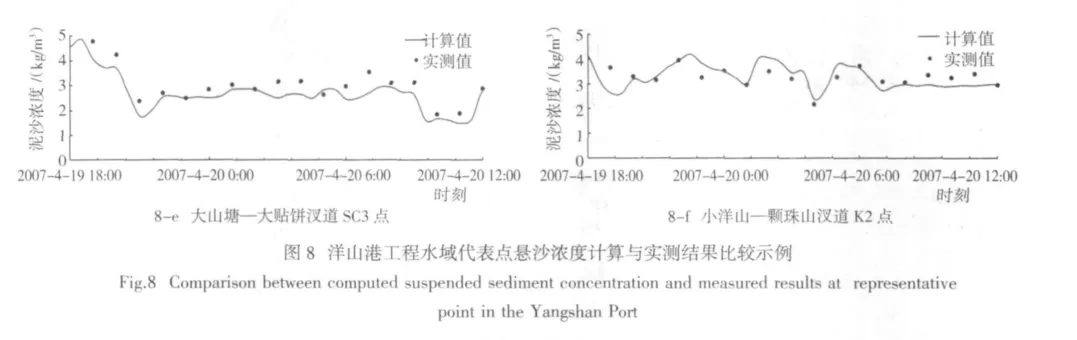
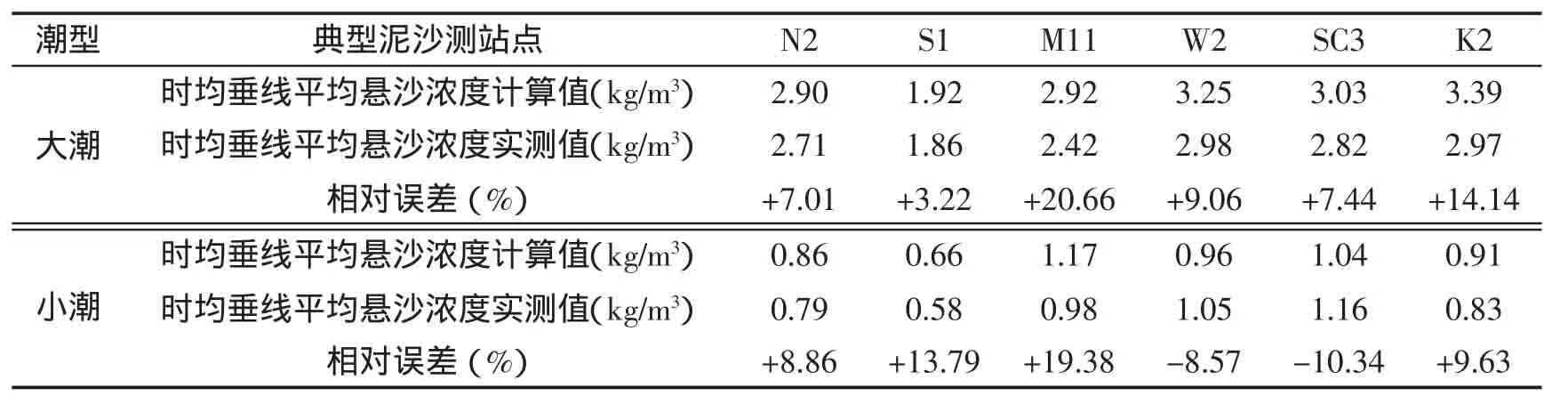
對泥沙沉降速度,理論上與泥沙粒度有關。對于泥沙粒徑d<0.01 mm的泥沙,將發生絮凝現象,絮凝沉速在0.000 3~0.000 6 m/s,可直接取絮凝沉速為0.000 4 m/s;而泥沙粒徑在0.03 表1 泥沙沉降速度Tab.1 Velocity of sediment 對于二維模型中泥沙水平擴散系數ε,一般是基于渦粘系數類比公式計算而得,即ε=λεt(εt為渦粘系數),渦粘系數比例因子在0.5~1.5。 在泥沙的沉降速度已確定的條件下,分別計算了λ為0.5、1.0、1.5時的懸沙濃度值,結果幾乎沒有什么變化,表明ε對懸沙濃度計算影響很小,數值計算時可取渦粘系數比例因子λ為1.0。 對于控制侵蝕速度的比例值E,硬泥層一般取0.000 1(kg·m-2)/s,軟泥層可0.000 005~0.000 02(kg·m-2)/s取值,分別取軟底床的為0.000 005(kg·m-2)/s、0.000 01(kg·m-2)/s、0.000 015(kg·m-2)/s、0.000 02(kg·m-2)/s 4 組值進行懸沙濃度的計算,結果表明懸沙濃度變化很小,即表明E對懸沙濃度計算的影響不大,可直接取值0.000 02(kg·m-2)/s。 對于硬底床的侵蝕指數n,一般取10;對于軟底床的侵蝕系數α通常在4~20變化,對于淤積偏重的地區可選擇下限值4,侵蝕偏重的地區取20,而對于沖淤相當的可在中間挑選一個值即可。 綜上所述,泥沙沉降速度ω、泥沙擴散系數ε、控制侵蝕速度的比例值E、軟底床的侵蝕系數α、硬底床的侵蝕指數n,在懸沙濃度的數值計算中分別按照上述方法取值,對結果的影響不大。由此篩選出對懸沙濃度計算影響最大的3個參數分別為:床面糙率、河床淤積物的干密度以及床層間的泥沙轉換率。 下面分別討論床面糙率、河床淤積物的干密度、床層間的泥沙轉換率對懸沙濃度計算結果的影響。 床面糙率是描述海床對水流阻力的參數,可采用謝才系數、曼寧系數、尼古拉茲糙率等表示。當采用尼古拉茲糙率時,床面糙率依賴于床面形狀和底床泥沙顆粒的粒徑。進行含沙量計算時,可將計算范圍的局地床面形狀均值化,即床面糙率僅依賴底床泥沙顆粒的粒徑,其值可按n倍泥沙顆粒的粒徑計算,即k=nd。 在擴散系數ε等其他5個參數固定不變、且按照2.1節所述取值的條件下,分別選取床面糙率k=1.0 d、2.5 d、4.0 d、5.5 d,分析床面糙率k的取值變化對懸沙濃度的影響。 根據經驗,當d<0.5 mm時,有些學者直接取k=0.001 m。對于洋山港工程水域,底質平均中值粒為0.037 mm。因此,在討論床面糙率對懸沙濃度的影響時,也將k=0.001 m作為一種處理方法,與k=nd的處理方法進行比較。圖3給出了采用不同的床面糙率時懸沙濃度的計算結果。 由圖3可見,對于床面糙率,若直接取0.001 m,計算得到的懸沙濃度隨時間的變化過程與實測結果差別較大。若床面糙率按照粒徑的倍數來計算,當糙率取不同的粒徑倍數時,計算的懸沙濃度和實測濃度的誤差也將隨之變化(表2)。 將表2的不同粒徑倍數情況下所計算得到的平均懸沙濃度和實測的平均懸沙濃度進行對比,將粒徑倍數值與誤差關系繪出曲線(圖4)發現,當選取k≈2 d時,計算的平均懸沙濃度和實測濃度的誤差最小,即床面糙率的最佳取值應為k≈2 d。 表2 床面糙率對平均懸沙濃度值的影響匯總Tab.2 Influence of bed roughness on value of suspended sediment concentration 河床淤積物的干密度是一個重要的泥沙參數,對于沖淤體積和重量的換算、泥沙起動、河床沖刷及水流挾沙能力等均有相當重要的影響[6],干密度是不隨時間變化的。河床的最上層為最弱層,主要是浮泥或新淤積的泥沙,稱之為軟泥;其下面層的密度及強度都不斷遞增,稱之為硬泥。 河床淤積物的干容量與孔隙率成反比,孔隙率與泥沙粒徑成反比,河床淤積物的干容重隨著時間的變化很小,根據大量的實驗得出:軟泥的干密度[7]會在100~400 kg/m3浮動,具體的數值是取決于各自的環境,和新淤積泥沙的濕容重也有密不可分的關系,而硬泥則是由底質粒徑按照公式γd=1 750×d0.183[8]計算,其中粒徑的單位為mm。 港區的海床分為兩層:上層為軟底床,即泥沙最新輸運落淤的床層,分別計算了干密度為150 kg/m3、250 kg/m3、400 kg/m3這3種不同的密度量級(圖5)。區域中新落淤的泥沙干密度取250 kg/m3時計算的泥沙濃度和實測值擬合較好,其他的誤差在10%~60%不等;下層為硬底床,按照底層粒徑和公式γd=1 750×d0.183計算干密度。 在模擬計算時,通常將海床分為可動層和固結層兩層,層間的泥沙在動力作用下的泥沙交換量的多少采用泥沙轉換率描述。該參數對于研究泥沙運動機理、考慮床沙和運動泥沙的關系、計算懸沙濃度及海床沖淤強度等均為最重要影響參數之一。其取值范圍一般在0.1~0.001(kg·m-2)/s,該范圍上、下限量值上相差100倍,各個取值對懸沙濃度計算結果的影響是顯而易見的。 在此,與分析床面糙率k對懸沙濃度影響一樣,在探討泥沙轉換率對懸沙濃度影響時,也將擴散系數ε等其他 5 個參數固定不變(按照 2.1 節所述取值),分別選取 m 為 0.000 1(kg·m-2)/s、0.001(kg·m-2)/s、0.01(kg·m-2)/s、0.1(kg·m-2)/s,計算了 4 組不同的轉換率對應的懸沙濃度隨時間的變化過程,與實測結果的比較匯總于圖6。 由圖 6 可知,當 m 取值為 0.01(kg·m-2)/s和 0.1(kg·m-2)/s時,即固結率較高時,由于大部分懸沙落於到床面后固結,使得懸沙濃度大幅度降低。換言之,懸沙濃度模擬計算時,如果過高估計了泥沙轉換率,將使得計算懸沙濃度小于實際懸沙濃度。反之,計算懸沙濃度將大于實際懸沙濃度。計算表明,當泥沙轉換率為0.001(kg·m-2)/s時,模擬的泥沙濃度和實測的泥沙濃度值擬合最好。即最佳床層間的泥沙轉換率為0.001(kg·m-2)/s。 對于影響懸沙濃度計算的各個泥沙參數,采用前節泥沙參數的取值方法,分別取泥沙沉降速度:絮凝沉速ω=0.000 4 m/s,非絮凝沉速按表1取值;泥沙擴散系數:渦粘系數比例因子λ=1.0;控制侵蝕速度的比例值:硬泥層 E=0.000 1(kg·m-2)/s,軟泥層 E=0.000 02(kg·m-2)/s;硬底床的侵蝕指數:n=10;軟底床的侵蝕系數:對于港區南部(淤積)α=4,對于港區北部(沖刷)α=20;床面糙率:k=2 d;泥沙干密度:對軟底床γd=250 kg/m3;對硬底床γd=1 750×d0.183;床層間的泥沙轉換率:m=0.001(kg·m-2)/s。 選定上述泥沙參數后,對洋山港全水域各特征代表點的懸沙濃度分別進行數值計算,并與實測結果進行對比。選取的代表點位置分布在洋山港外南北附近、港區、汊道等典型水域,代表點的具體位置見圖7。圖8給出了各代表點垂線平均懸沙濃度計算和實測結果比較示例。 圖 8-a 為小洋山北部 N2 點(北緯°39′26.54″,東經 2°04′04.85″)大潮期間垂線平均含沙量時間變化過程實測結果和計算結果的比較示例;圖 8-b~圖 8-f依次為大洋山南部 S1 點(30°33′19.14″,122°04′00.86″)、三期碼頭中部 M11 點(30°36′39.82″,122°04′30.31″)、西口門中部 W2 點(30°37′32.10″,122°00′13.05″)、大山塘—大貼餅汊道 SC3 點(30°35′30.58″,122°02′25.58″)、以及小洋山一顆珠山汊道 K2 點(30°38′41.28″,122°02′23.38″)的大潮期間垂線平均含沙量時間變化過程計算結果和實測結果的比較示例。表3給出了上述各代表點大潮和小潮期間的時均垂線平均含沙量計算與實測值的比較。 表3 洋山港工程水域典型泥沙測點時均垂線平均懸沙濃度值的計算值與實測值比較Tab.3 Comparison between computed vertical suspended sediment concentration in the average time and measured results at representative point in the Yangshan Port 由圖8和表3的比較可知,在洋山港周圍水域,按照前述推薦的各參數取值,計算得到的含沙量濃度隨時間變化過程及在一個潮周期內的時均值與實測結果的吻合程度是令人滿意的。 基于經過實測資料驗證的二維水動力模型,在較準確模擬潮流動力的基礎上,對于影響懸沙濃度計算有關的8個參數通過數值計算的方法:首先篩選出影響最大的3個參數為床面糙率、河床淤積物的干密度、床層間的泥沙轉換率;然后在其各個參數取值的可變范圍內,分別調整各個參數的取值,計算對比得到上述3個參數的最優取值。最后,就洋山港實際工程進行了懸沙濃度模擬計算,驗證了所選擇參數的可靠性。 研究表明,對于以潮流為主要環境動力的淤泥質海床而言,泥沙沉降速度可通過物理模型試驗或較為成熟的經驗公式計算得到較為可靠的數值;泥沙擴散系數,控制侵蝕速度的比例值,軟底床的侵蝕系數,硬底床的侵蝕指數等對懸沙濃度的影響較小。對于床面糙率、軟底床淤積物的干密度、床層間的泥沙轉換率,最佳取值分別為 2 d、250 kg/m3、0.001(kg·m-2)/s。 [1]ZUO S H,ZHANG N C,LI B,et al.Numerical Simulations of Tidal Current&Sediment and Sea Bed Erosion and Deposition for Yangshan Deep-water Harbor of Shanghai[J].International Journal of Sediment Research,2009,24(3):287-298. [2]左書華,張寧川,張征.島群海域環境下泥沙運動及地形沖淤變化數值模擬研究[J].泥沙研究,2011(2):1-8.ZUO S H,ZHANG N C,ZHANG Z.Numerical modeling of sediment transport and seabed erosion and siltation in archipelago sea area[J].Journal of Sediment Research,2011(2):1-8. [3]李文丹,李孟國,龐啟秀.臺山核電站取排水工程潮流泥沙數值模擬研究[J].水道港口,2011,32(2):94-100.LI W D,LI M G,PANG Q X.The tide and sediment numerical simulation study of Taishan nuclear power plant project[J].Journal of Waterway and Harbor,2011,32(2):94-100. [4]XIN W J.Computational Techniques of 2D Tidal Flow in Estuaries and Bays[J].China Ocean Engineering,1995,9(4):395-404. [5]曹祖德,楊樹森,楊華.粉沙質海岸的界定及其泥沙運動特點[J].水運工程,2003,352(5):15-20.CAO Z D,YANG S S,YANG H.Definition of silt-sandy beach and its characteristics of sediment movement[J].Port&Waterway Engineering,2003,352(5):15-20. [6]潘慶燊.三峽工程泥沙問題研究[M].北京:中國水利水電出版社,1999. [7]韓其為,王玉成,向熙瓏.淤積物的初期干容重[J].泥沙研究,1981(1):1-6.HAN Q W,WANG Y C,XIANG X L.Initial specific weight of deposits[J].Journal of Sediment Research,1981(1):1-6. [8]羅肇森.潮汐通道口攔門沙航道的淤積計算[J].海洋工程,1992(3):10-18.LUO Z S.Prediction of sedimentation for the navigation channel of a tidal inlet with mouth bay[J].Ocean Engineering,1992(3):10-18.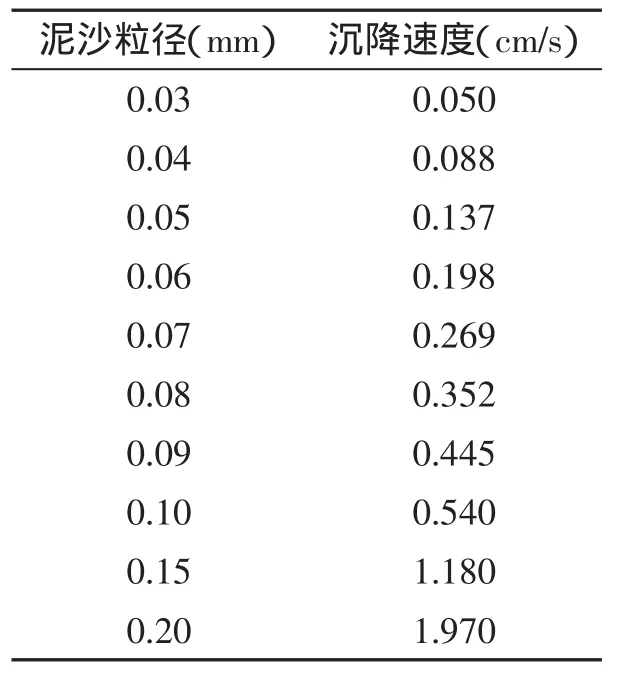
2.2 床面糙率k

2.3 河床淤積物的干密度

2.4 床層間的泥沙轉換率
3 懸沙濃度計算在洋山港實際工程中的驗證


4 結語

