一種新的T-S模型混合辨識算法

盧鴻謙，宋清南，黃顯林，高曉智 ，2

(1.哈爾濱工業大學控制理論與制導技術研究中心，150001哈爾濱，luhongqian@163.com;2.Aalto大學電氣工程系，00076 Espoo)

一種新的T-S模型混合辨識算法

盧鴻謙1，宋清南1，黃顯林1，高曉智1，2

(1.哈爾濱工業大學控制理論與制導技術研究中心，150001哈爾濱，luhongqian@163.com;2.Aalto大學電氣工程系，00076 Espoo)

提出一種新型混合辨識算法HIA，以解決傳統T－S模型辨識方法中所存在的不完全優化問題，如FCM與最小二乘法相結合的辨識方法就存在這樣的問題.HIA通過將FCM、和聲搜索算法以及最小二乘法相結合，并引入了誤差反饋機制，以實現對所有參數的整體優化，并避免陷入局部極小點.論文將HIA應用到陀螺穩定平臺的T－S模型辨識中，通過與傳統辨識方法比較MSE值可以看出，HIA能夠獲得更高的辨識精度.這表明，對于實際的非線性系統，HIA能夠有效解決傳統辨識方法的不完全優化問題.

T－S模型辨識;混合辨識算法;誤差反饋機制;陀螺穩定平臺

近年來，有關 T－S 模型［1］辨識方法的研究取得了很大的進展，其包括結構辨識與參數辨識2個方面.在結構辨識方法中，基于RC原則法、前向選擇法、后向選擇法等用于輸入變量的選擇;而輸入空間劃分方法則有網格劃分法、聚類方法［2］等;在參數辨識方法中，一般先通過網格劃分或模糊聚類等方法確定前件參數，而后采用線性優化方法如最小二乘法［3］、梯度下降法等對后件參數進行優化.這些方法只基于一組未優化的前件參數來優化后件參數，回避了非線性優化問題，辨識精度難以提高.而神經網絡、遺傳算法等各種隨機搜索算法的出現，使得前件及后件參數的整體優化得以實現.這些算法的思路主要有2種，一種是直接從整體的參數空間出發，對前件參數及后件參數進行整體優化，這種方法的效率不高，精度也無法得到保證;另外一種則是先采用傳統的辨識方法確定前件及后件參數，然后利用隨機搜索算法對模型規則數進行增減.而本文所設計混合辨識算法HIA則將和聲搜索(HS)算法［4］、模糊聚類(FCM)算法［5］與最小二乘法有機結合，對參數進行整體優化，并利用傳統辨識方法的優勢，避免非線性優化問題，使辨識精度以及辨識效率同時得到保證.文獻［6］從理論上對該算法進行了闡述及仿真，本文在此基礎上，通過陀螺穩定平臺的T－S模型辨識，來驗證HIA在解決傳統辨識算法缺陷上的有效性.

1 T－S模型辨識原理

T－S模型是一種描述復雜非線性過程的數學模型，其模糊規則庫由N條規則組成，其中第j條規則如下:

如果uk1∈Aj1，且uk2∈Aj2，…，ukm∈Ajm，那么，

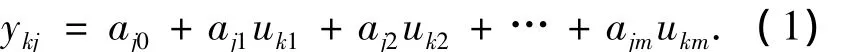
其中，Aji(i= 1， 2，…，m)為模糊集;uki(i= 1， 2，…，m)為m維輸入;ykj為第j條規則對應于第k個輸入的輸出．在此基礎上，應用“取小”或“乘積”以及“加權平均”操作解模糊化，可計算得到輸出值．

以MISO系統為例，考慮如式(2)所示指標函數［7］:

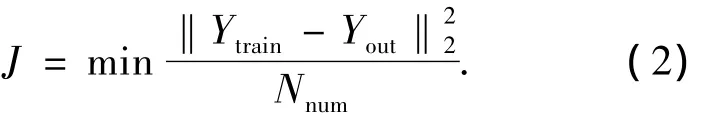
其中，Nnum為訓練數據對個數;Ytrain為訓練數據輸出向量;Yout為辨識輸出向量，其第k個分量yok由(3)描述:

式中m為輸入維數，采用取小操作解模糊化及高斯型隸屬函數劃分輸入空間．隸屬函數如式(4)所示:

其中:j= 1， 2，…，N;i= 1， 2，…，Nnum;cji為第j個聚類中心的第i維分量;σji為第j個聚類的聚類方差的第i維分量．

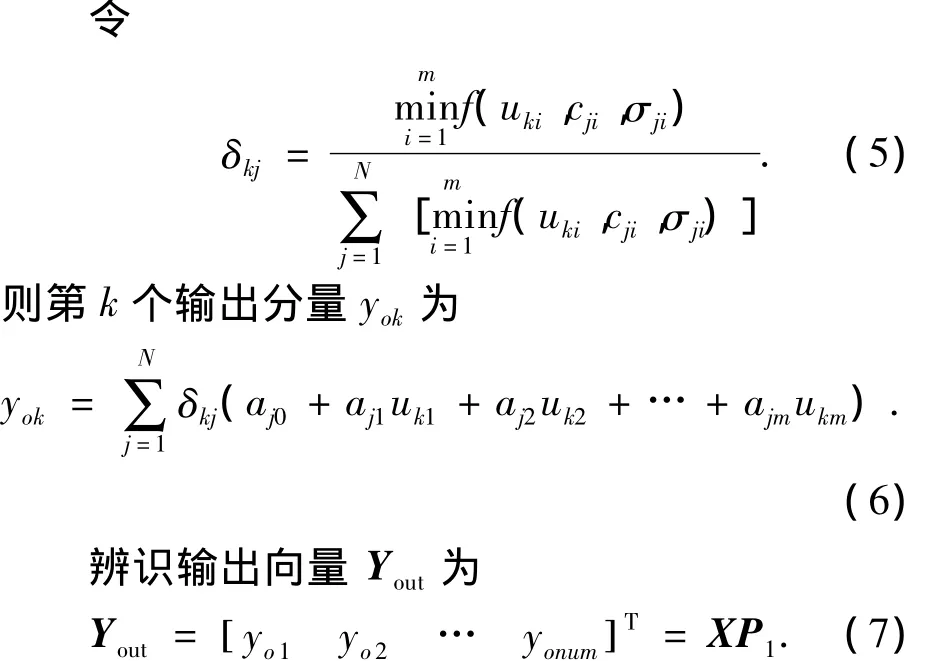
其中，矩陣X與參數向量P1的表達式如下:

構造參數向量Pc和Pσ，如下所示:

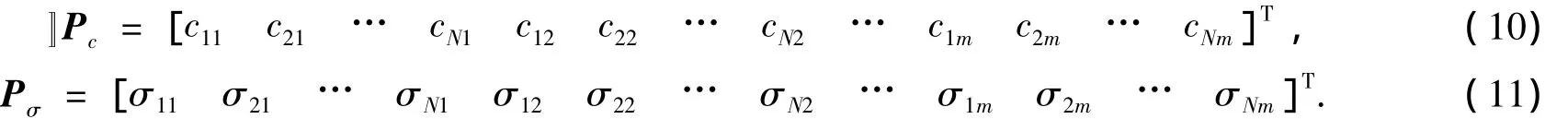
從式(7)可得，當Pc和Pσ未知時，對式(2)的優化是1個高維非線性函數優化問題．在傳統辨識方法中，一般先確定Pc和Pσ，并通過線性估計方法求得最優后件參數向量P1，這種做法的目的是為了避免高維非線性函數優化的問題，但它一般只能得到降維空間意義下的部分參數最優值．HIA的目標在于既能實現總體參數向量P的優化，同時又避免高維非線性函數優化的問題．

2 HIA辨識算法原理

2.1 HIA總體設計思想

HIA旨在解決傳統辨識算法中所存在的缺陷——不完全優化問題.從式(1)～(11)可知，TS模型辨識辨識最終可歸結為如下式所示的目標函數:

這是1個高維非線性優化問題．如果通過隨機搜索方法實現參數向量Pc及Pσ向著指定參數空間內的最優點前進，則對參數向量P1的優化就可通過最小二乘法實現，這樣就避免了高維非線性優化問題，使問題得以簡化，這即是將HS算法引入到T－S模型辨識過程的目的.也是HIA的理論基礎之所在.

具體而言，HIA將和聲搜索(HS)算法、模糊C均值聚類(FCM)法以及最小二乘法有機結合，三種子算法的功能如下:利用FCM算法實現模型前件參數空間的初始劃分，HS算法實現對前件參數空間即Pc及Pσ的尋優，而最小二乘法則在HS搜索算法的基礎上對后件參數空間進行優化.通過這樣的子算法組合，使得混合辨識算法達到既避免高維搜索問題，又能實現模型參數辨識全局優化的目的.由于T－S模型辨識的目標函數具有其獨特的性質，使得HIA方法能夠取得良好的辨識效果.下面分別介紹HIA中各子算法的原理.

2.2 HIA各子算法概述

和聲搜索算法模擬和聲創作過程尋找函數全局最優點.其尋優過程如下:

1)隨機生成HMS個解向量，并計算其適應度值，構建和聲解庫Harmony Memory;

2)生成新的解向量，以概率HMCR對和聲解庫中的解向量進行隨機組合;以概率PARGN對其分量以幅度BW調整;以概率1－HMCR隨機生成1個解向量;

3)計算其適應度值，更新和聲解庫，并返回步驟2)，直至達到最大的搜索次數IN．

算法中有幾個重要參數需通過反復嘗試來確定．如 HMS、HMCR、PARGN、IN 及 BW 等，圍繞這些參數的調節機制，有許多經改善后和聲搜索算法．本文HIA中，PARGN和BW采用如下式所示的變化規律［8］:

其中n為當前搜索次數．如此調節的目的是使搜索算法在搜索初期以較大概率及較大的范圍進行調整，減小算法陷入局部極小點的概率．HIA中和聲搜索空間的初始參考點由FCM算法給出.

采用FCM對前件空間進行劃分的好處是可根據實際輸入量的空間分布來進行前件空間的初始劃分，且可以避免規則爆炸問題.當廣義輸入變量維數不高，且其空間分布范圍已知時，可以用網格劃分方法來代替FCM的，只是此時后件的規則數要增加一些.FCM算法將數據點按式(12)所示目標函數歸類［9］.

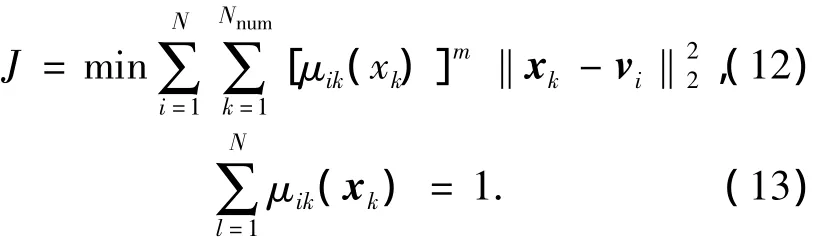
其中，m≥ 1，一般取m=2．當對Nnum個數據點進行N個劃分時，點xk以μik隸屬于第i個聚類中心vi，μik滿足如式(13)所示的約束條件．通過拉格朗日乘子法求解帶約束的函數優化問題，J值可通過迭代方法求得．迭代公式如下所示［10］．

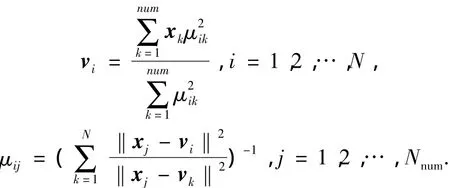
FCM聚類獲得初始前件參數后，初始后件參數以及該組解向量對應的適應度值可通過最小二乘法來獲得.遞推最小二乘法為

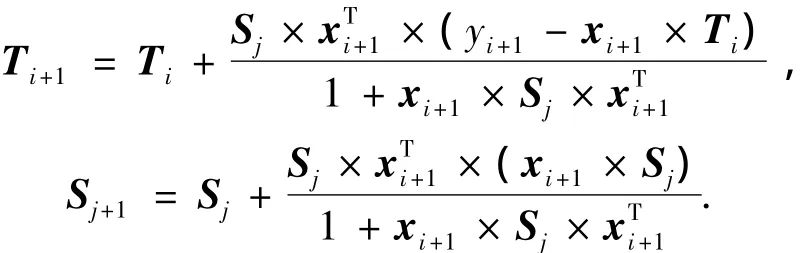
其中，Ti(i= 0， 1，…，Nnum－1)為式(9)所示的后件參數向量;Si為增益矩陣;xi+1為X的第i+1行;yi+1為訓練數據輸出Ytrain的第i+1個分量．遞推初始參數 T0= 0，S0=1010I，IN×(m+1)，N×(m+1)為單位陣．

2.3 HIA流程圖

HIA將前件參數與后件參數綜合優化，同時又利用傳統辨識方法的優點，在隨機搜索方法的基礎上引入最小二乘算法加以約束，不僅避免了高維搜索，搜索精度也有了可靠保證.其中，HS算法的引入是HIA之所以能實現高效的高維參數優化的關鍵.其模擬音樂家創作和聲的過程引導著參數向量Pc及Pσ向著指定參數空間內的最優點前進，從而給參數向量P1的優化創造了條件．HIA流程圖如圖1所示.

3 陀螺穩定平臺建模

待建模系統是光纖陀螺穩定平臺.目標是利用采集到的實際陀螺穩定平臺輸入輸出數據，辨識得T－S模型.

本文欲建立系統的外環框架轉動角速度與輸入電壓之間的關系.待辨識系統處于開環狀態，輸入端為計算機，輸出端為外環框架上固連的光纖陀螺.框架上帶有相應的光電編碼器，可以測出外環框架轉過的角度，但由于該光電編碼器的精度較低，通過其所測量角度信號進行差分得到框架轉動角速度的方法是不可取的，因為這種方法會造成噪聲的放大.而外環上所固連的光纖陀螺是可以直接測量到外環的轉動角速度的，所以本文在建立該系統的T－S模型時，將光纖陀螺做為1個測量角速度的傳感器來使用.

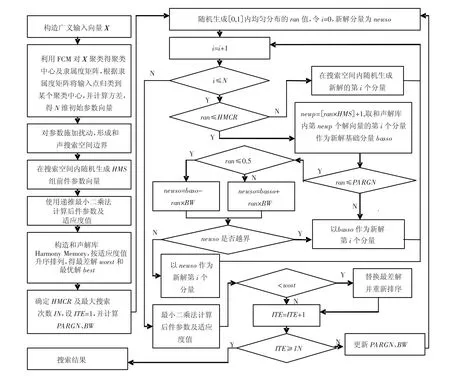
圖1 HIA算法流程

實際待辨識對象為1個陀螺穩定平臺，以其外環作為辨識對象，光纖陀螺輸出外環的轉動角速度.該系統內的非線性因素很多，如力矩電機的死區、飽和及遲滯特性;傳動齒輪之間的間隙，陀螺內部的各種非線性特性以及由于外環質量沿對稱軸分布不均所導致的慣量不平衡等干擾因素，使得對該系統進行合理準確的描述變成1個不容易實現的任務.對于這樣的非線性系統，如果采用1個線性系統如慣性環節或者階次更高的環節對其進行描述，所得到的辨識精度一般是無法滿足要求的.本文采用混合辨識算法HIA建立該陀螺穩定平臺的T－S模型，以實現對該系統更加準確合理的描述，并取得了很高的辨識精度.

陀螺穩定平臺處于半實物仿真平臺中，可通過MATLAB采集到帶噪聲的光纖陀螺轉速輸出數據.建模激勵信號采用高斯白噪聲，該信號由Simulink中的 Signal Builder生成，其頻率為10 Hz，方差為 1，均值為 0.信號采樣時間為15 ms，共采集4 000組I/O數據，歷時60 s.

利用光纖陀螺輸出轉速向量V及激勵信號向量U構造廣義輸入向量

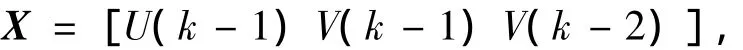
輸出向量為V(k)，如此選擇輸入向量的意義為，k時刻的框架轉速輸出與k－1時刻的激勵信號、轉速輸出及k－2時刻的轉速輸出有關，而與k時刻的激勵信號無關．由于框架存在慣性，k時刻的激勵信號只能影響下一時刻的轉速輸出．基于這樣的考慮，可構造3 998組廣義輸入輸出數據對，其中3 000組用于模型辨識，其余998組用于驗證模型泛化性．HS初始參數設置如表1所示.其中，IN為搜索次數;DIS表示在允許邊界內對前件參數施加±30%的擾動，擾動施加以后，聚類中心c不超過區域Ω;聚類方差σ在Ω的10% ～75%區域內;最大的搜索幅度BWmax不超過初始設定邊界的40%;最小搜索幅度BWmin不小于0.001．這些初始參數是多次實驗取得的經驗值.擾動及聚類方差范圍的限定，是為減小規則不完備現象出現的概率.而搜索幅度的限定則是為了減小由于搜索幅度過大使參數超出限定邊界的概率，以及由于搜索幅度過小而陷入局部極小點的概率.陀螺穩定平臺實驗數據表如表2所示(取5位有效數字).表中數據為均方誤差(MSE)值，其含義如式(2)所示.其中的傳統辨識算法由FCM及最小二乘法構成.

表1 和聲搜索初始參數

表2 陀螺穩定平臺實驗數據

表2實驗數據顯示，針對實際的陀螺穩定平臺，相比于傳統的辨識算法，HIA在提高辨識精度上具有明顯的效果.驗證了HIA對于實際系統具有提高辨識精度的能力.圖2～5分別給出了6個聚類數下的第1次實驗中，由HIA所得到的辨識曲線及辨識誤差曲線、泛化性驗證曲線及驗證誤差曲線.圖2中實線表示采樣輸出，點劃線表示辨識輸出;圖4中實線表示采樣輸出，點劃線表示已辨識T－S模型的預測輸出.

圖2 辨識曲線

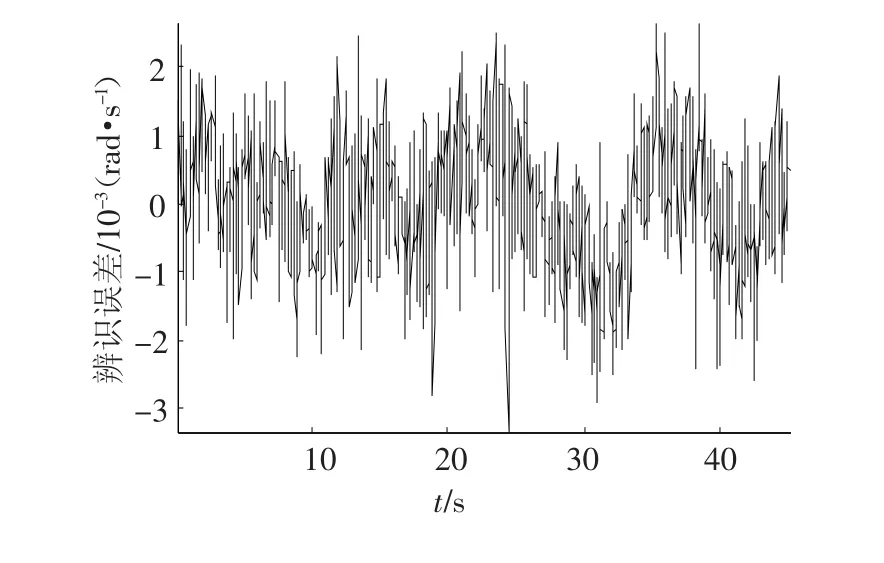
圖3 辨識誤差曲線

圖4 泛化性驗證曲線

圖5 驗證誤差曲線

4 結論

從陀螺穩定平臺T－S模型辨識的結果來看，對于實際的非線性系統，HIA能夠顯著提高T－S模型辨識精度.這也充分反映了傳統的將前件和后件參數分開辨識的方法是存在本質缺陷的，而HIA則很好的彌補了這種缺陷.HIA將隨機優化算法與確定性優化算法相結合，實現了對全局最優點的全維搜索，同時又避免了高維搜索問題，使參數的收斂速度加快，且使辨識精度得到了很大的提高.當然，由于HIA對廣義輸入向量的分布是有要求的，且其辨識過程需要一定的時間，所以HIA可重點應用于離線辨識或者慢時變系統模型辨識中，且其要求所選廣義輸入向量具有相對較為均勻的分布.另外，算法中的初始參數設置對最終的尋優結果有著很大的影響，如何合理的確定算法中的初始參數，使辨識模型的精確性、解釋性、完備性及泛化性都得到更好的保證，也將是本文下一步所要研究的內容之一.

［1］TAKAGI T，SUGENO M.Fuzzy identification of systems and its application to modeling and control［J］.IEEE Transaction on Systems，Man and Cybernetics， 1985，15(1):116－132.

［2］SUGENO M，YASUKAWA T.A fuzzy－logic－based approach to qualitative modeling［J］.IEEE Transaction on Fuzzy Systems， 1993，1(1):7 －31.

［3］趙志剛，呂恬生，王庚.基于 Takagi－Sugeno模糊模型的小型無人直升機系統辨識［J］.上海交通大學學報， 2008，42(4):856－860.

［4］KANG S L，ZONG W G.A new structural optimization method based on the harmony search algorithm ［J］.Computers ＆ Structures， 2004，82(9/10):781 －798.

［5］LáZARO J，ARIAS J，MARTíN J L，et al．Implementation of a modified Fuzzy C－Means clustering algorithm for real－time applications［J］.Microprocessors and Microsystems， 2005，29(8/9):375 －380.

［6］黃顯林，宋清南，班曉軍，等.一種基于和聲搜索算法的T－S模型辨識方法［C］//第二十九屆中國控制會議論文集.北京:中國自動化學會控制理論專業委員會，2010:1224－1229.

［7］PARK M，JI S W，KIM E.A new approach to the identification of a fuzzy model［J］.Fuzzy Sets and Systems， 1999，104:169－181.

［8］TAHERINEJAD N.Highly reliable harmony search algorithm［C］//European Conference on Circuit Theory and Design.Antalya:ECCTD，2009:818－822.

［9］HUNG Mingchuan，YANG Donlin.An efficient fuzzy C－means clustering algorithm［C］//IEEE International Conference on Data Mining.Piscataway:IEEE，2001:225－232.

［10］CHEN Musong，WANG Shinnwen.Fuzzy clustering analysis for optimizing fuzzy membership functions［J］.Fuzzy Sets and Systems， 1999，103:239 －254.

A novel hybrid T-S model identification algorithm

LU Hong－qian1，SONG Qing－nan1，HUANG Xian－lin1，GAO Xiao－zhi1，2

(1.Center for Control Theory and Guidance Technology，Harbin Institute of Technology，150001 Harbin，China，luhongqian@163.com;2.Dept.of Electrical Engineering，Aalto University，00076 Espoo，Finland)

To overcome the drawback of regular T－S model identification techniques，such as the FCM and least－squares method，a new Hybrid Identification Algorithm(HIA)is proposed in this paper.The HIA can simultaneously optimize all the model parameters and avoid being trapped into the local minima by merging the FCM，Harmony Search(HS)and the least－squares method together and using the error feedback mechanism.Our HIA is employed in the T－S modeling of the Gyro－stabilized platform.By comparing the MSE peformance，the HIA can indeed yield a superior MSE performance over the conventional identification methods.The identification results show that the HIA can effectively overcome the incomplete optimization problem of the conventional identification methods.

T－S model identification;hybrid identification algorithm;error feedback mechanism;Gyro－stabilized platform

TP18

A

0367－6234(2011)09－0001－06

2010－04－22.

國家自然科學基金資助項目(60874084)，芬蘭科學院基金資助項目(135225).

盧鴻謙(1975—)，男，講師;

黃顯林(1955—)，男，教授，博士生導師;

高曉智(1972—)，男，教授，博士生導師.

(編輯 張 宏)