IR-UWB近距離實孔徑成像系統分辨率

黃冬梅，張欽宇

(哈爾濱工業大學深圳研究生院，518055深圳，huangdongmei@126.com)

IR-UWB近距離實孔徑成像系統分辨率

黃冬梅，張欽宇

(哈爾濱工業大學深圳研究生院，518055深圳，huangdongmei@126.com)

為了解決傳統“窄帶、遠場”分辨率計算公式不再適用于超寬帶極窄脈沖(IR－UWB)近距離實孔徑成像系統的問題，提出了一種新的分辨率的計算方法.通過對IR－UWB近距離成像原理的分析，推導了單天線在距離向及橫向分辨率的解析表達式，結合圖像重建過程中信號疊加原理，提出了一種實孔徑均勻線陣分辨率的計算方法.通過對理想點目標成像結果的數值仿真，驗證了該分辨率計算方法的正確性.

分辨率;超寬帶極窄脈沖;實孔徑天線陣;近場;成像

近些年，超寬帶極窄脈沖(Impulse Radio Ultra－Wide Band，IR－UWB)實孔徑成像系統，如探底雷達、穿墻成像系統等備受關注［1－2］.其中分辨率的計算對成像系統設計、算法實施和實際成像過程非常重要.然而受到超寬帶、近距離、實孔徑的影響，系統工作于“窄帶、遠場”的假設條件不再成立，傳統分辨率計算公式［3－4］不再適用.此外，在典型的近場IR－UWB實孔徑成像系統中，為表示方便，通常采用類似于合成孔徑雷達中的直角坐標系表示，認為天線陣軸線延伸的方向為橫向，而與天線陣軸線垂直的方向為距離向，嚴格的講這與傳統的橫向、距離向的定義有區別.并且目標不再始終位于孔徑中心線方向，當目標不在天線陣中心線方向時，目標的圖像會出現一定程度的偏斜，此時通過傳統的角度分辨率來分析與天線陣孔徑平行的橫向分辨率亦不方便［5］.

文獻［6－7］基于非相干三角定位技術分別對超寬帶雷達系統的分辨率進行了定性和定量的分析，指出了“有限距離”下的距離分辨率是空間變化的，但是沒有給出有限距離下的方位向分辨率表達式，并且沒有考慮利用由多個陣元組成的天線陣進行探測成像時系統的分辨率.文獻［8－10］從波束形成的角度分析了IR－UWB陣列的遠場角分辨率，利用角分辨率分析方位分辨率，并給出了方位向分辨率的粗略計算公式.文獻［11－12］推導了“大方位積累角”沖激SAR的方位向分辨率估計公式，但是僅給出了天線瞄準線方向的分辨率計算公式，且基于目標距離相對于天線陣孔徑比較大的假設條件，公式并不能完全反映近場成像系統分辨率的空間變化特性.

目前對分辨率的研究多通過角分辨率來分析橫向分辨率，并且沒有充分考慮近場、實孔徑條件的影響.因此，本文基于理想的系統、點目標模型［13］對IR－UWB近距離實孔徑成像系統進行分析，提出了一種新的IR－UWB近場實孔徑成像系統分辨率的計算方法，并利用數值仿真驗證了該方法的正確性.對IR－UWB近距離成像系統的設計具有重要的指導意義.本文在討論分辨率時，以圖像中強度相同的2個目標點峰值之間的凹陷大于 －3 dB 的情況視為正確分辨［14－15］.

1 IR－UWB近距離實孔徑成像系統分辨率計算

不考慮信號傳播過程中的波形失真，假設探測環境為自由空間，天線為全向理想點天線，發射天線為單個天線，發射IR－UWB信號，接收天線為均勻線性陣列，陣列孔徑為L，陣元間距為d，陣元數量為N，發射天線位于接收天線的中心位置.以發射天線為原點，接收天線陣為x軸建立直角坐標系，則發射天線的坐標為xT=( 0，0);接收天線陣中各陣元的坐標為 xi=(xi，0)，i= 1， 2，…，N/2.通常限定探測區域為y＞0的半區.常用的成像方法為后向投影(BP)算法［ 2，16］.假設在探測區域(xp，yp)處有1 個理想的點目標 δ(xp，yp)，經過BP成像處理后，由單個天線接收到該點目標回波恢復出的圖像為具有一定寬度的一段橢圓，橢圓以發射天線和接收天線為焦點，接收信號的時間延遲對應的空間距離的一半為長軸.不同接收天線對應的“橢圓”相交于目標點的位置，在圖像空間疊加后產生1個峰值，便形成了改點目標的圖像.

1.1 單天線在x、y方向分辨率

設由天線xi=(xi，0)接收的點目標 xp=(xp，yp)的回波恢復的橢圓為eP，橢圓的焦點分別為發射天線xT和接收天線xi，長軸為

其中:τip為信號從發射天線傳播到點目標，再后向傳播到接收天線的雙程回波時延;dip為對應的雙程距離;RTp為點目標到發射天線的距離;Rip為點目標到接收天線的距離;v為電磁波在介質中的傳播速度.

若單個陣元對空間2個目標可以分辨，則要求接收的2個目標的回波信號在時間上可分辨.假如發射的IR－UWB信號的時間分辨率為Δτ=Tw，對應的雙程距離為Δdi=vTw.根據這個距離可以確定另外2個橢圓e1、e2，橢圓的焦點與eP相同，長軸距離分別為(dip－vTw)/ 2，(dip+vTw)/ 2，如圖1所示.在橢圓e1、e2上的目標回波與目標xp的回波在時間上剛好可以分辨，這2個橢圓共同決定了系統在xp點(圖1中P點)處各方向分辨率，稱這2個橢圓圍起的閉合區域(如圖中的陰影區)為不可分辨區.以橢圓的中心(xi/ 2，0)可以建立1個新的直角坐標系x'O'y'，根據坐標變換定理有

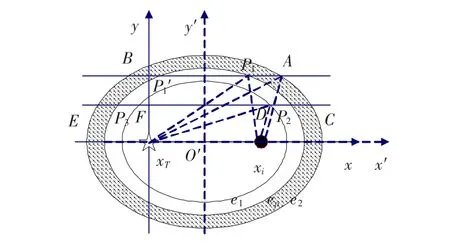
圖1 x方向分辯率

首先考慮x方向的分辨率，由于分辨率在正、負方向不一定相同，因此需分別考慮.過目標點做一與x軸平行的直線，如圖1所示，直線與橢圓e1，e2的交點即決定了目標點處x方向的分辨率.從圖1中可以看出，直線與橢圓e2一定存在2個交點，但是與橢圓e1可能相交，也可能不相交.根據直線與橢圓e1是否相交，將x方向分辨率的計算分為兩種情況:

1)直線與橢圓e1沒有交點，如點P1.此時，橢圓e1對x方向分辨率沒有貢獻.過目標點的直線與大橢圓e2相交于兩點A、B，這兩點分別決定了目標點處沿 +x及 －x方向的分辨率.

2)直線與橢圓e1有交點，如點P2.此時，直線有兩部分處在橢圓e1、e2確定的陰影區域中，利用天線陣中多個陣元的協作，可以很容易的去除與目標點相距較遠的直線段的影響，因此只考慮目標點所在的那部分直線段.直線分別與橢圓e2、e1相交于點C、D，這兩點分別確定了目標點沿 +x及 －x方向的分辨率.

當目標點的縱坐標yp＞b1時，屬于第一種情況.直線與橢圓e2相交于點A、B.將P的縱坐標代入式(1)，并令m= 2，消掉參考角度θ可以求得2點的橫坐標分別為其中x'p=xp－xi/2為目標點在新坐標系中的橫坐標.－x方向的分辨率為

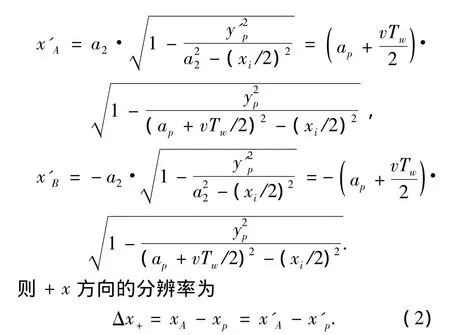
當yp≤b1時，屬于第二種情況.此時，直線段與橢圓e1、e2分別相交于兩點D、C或E、F，這與目標點的位置有關.當xp≥xi/2時，目標點位于圖1中P2位置，離目標點較近的兩個交點為C、D.將P的縱坐標代入式(1)，分別令m= 1， 2，消掉參考角度θ可得2點的橫坐標分別為

當xp＜xi/2時，目標點位于圖1中P3位置，離目標點較近的兩個交點為E、F，它們的橫坐標分別為

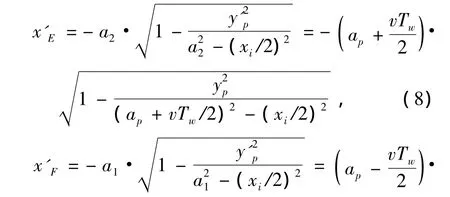
從式(2)～(11)可以看出，單個陣元的x方向分辨率分為 +x、－x方向，兩個方向的分辨率不一定相等，它們不僅與IR－UWB信號的時間分辨率Tw、傳播速度v有關，而且與目標位置xp和接收天線位置xi有關.

與x方向分辨率計算類似，過目標點做一與y軸平行的直線，根據直線與橢圓的交點可以確定單個陣元y方向分辨率.但需要注意成像系統中只對天線陣一側y＞0的探測區域感興趣，因此只考慮y＞0的半個橢圓與x軸形成的閉合區域，如圖2所示.根據直線與橢圓e1是否相交，y方向分辨率的計算同樣分為兩種情況.當目標點的橫坐標xp＞xi/2+a1或xp＜xi/2－a1時，直線與橢圓e1沒有交點，為第一種情況.當目標點的橫坐標xi/2－a1≤xp≤xi/2+a1時，直線與橢圓e1有交點，為第二種情況.具體的計算過程與x方向分辨率計算方法相同.y方向的分辨率同樣分為+y及－y方向，兩個方向的分辨率不一定相等，它們與IR－UWB信號的時間分辨率Tw、傳播速度v、目標位置xp和接收天線位置xi有關.

圖2 y方向分辯率

1.2 實孔徑均勻線陣近場分辨率

在成像系統中，為了獲得一定的信噪比，天線陣通常由多個陣元組成.由上述的分析可知，不同位置的陣元對同一目標的分辨率不同，因此，如何確定整個實孔徑天線陣實現的分辨率成為了一個難題.本節提出了一種新的分辨率計算方法.

受超寬帶波束形成中波束主瓣－3 dB寬度計算方法［8－9］的啟發，假設發射的 IR－UWB 信號為具有一定時間寬度的理想矩形脈沖，幅度為單位 1，不考慮幅度衰減，成像區域中有2個強度相同的點目標，由N個陣元組成的接收天線中各陣元接收到2個目標的回波信號，經過BP成像處理后分別在2個目標點的位置處疊加產生峰值，峰值幅度為N，而對于2個目標中間的區域，稱之為凹陷區域，當天線陣中陣元對2個目標可以分辨率時，該陣元接收的回波信號對凹陷沒有貢獻，而當陣元對2個目標不可分辨時，該天線接收的2個目標的回波信號對凹陷都有貢獻，即對凹陷處的貢獻的信號幅度為2.當有Nnr個陣元對兩目標無法分辨時，疊加后的圖像凹陷處的信號幅度為2Nnr.如果此時凹陷處能量剛為目標峰值能量的－3 dB，則兩個目標“剛好”可以分辨.實際上，在天線陣近場區域，單個陣元分辨率的變化范圍比較大，例如當天線陣孔徑長度為2 m時，xi=1的陣元對( 0，2)的 +x方向分辨率大約為xi=－1的陣元的3倍，此時若兩目標的距離剛好為xi=－1的陣元的可分辨距離，則xi=1的陣元接收的信號不僅對凹陷處有貢獻，還會對另一目標點處的信號產生影響，因此實際目標點峰值幅度將為N+Nnr.根據分辨率定義可得當2個目標剛好可以分辨時，Nnr與N的關系為

由于陣元數為整數，并且當2個目標可以分辨率時要求凹陷處的能量小于等于－3 dB，因此取

其中?·」表示向下取整.此時對兩目標可分辨的陣元數為Nr=N－Nnr.由此可見，當天線陣對2個目標可以分辨時，并不要求所有的陣元對2個目標都可以分辨，它允許一部分陣元(Nnr個)對2個目標無法分辨.組成天線陣的陣元數越多，允許對目標不可分辨的陣元數越多.

根據上述分析，可以得到實孔徑均勻線陣分辨率的計算方法為:

1)針對某個空間位置，計算天線陣中所有單個陣元在該點處的各方向分辨率;

2)對所有單個陣元在不同方向分辨率分別進行降序排列，選取第

個最大的分辨率值，該值即為天線陣在該點處對應方向上可實現的分辨率.

對于不同的陣元數N，根據式(12)計算的NΔ以及可分辨陣元數Nr如表1所示.從表1可以看出，當有N=3個陣元時，只要有2個陣元對目標可分辨，則天線陣對2個目標即可分辨，這與文獻［7］中的對角度分辨率的分析結果是一致的，并不需要所有的陣元對目標均可分辨.

表1 陣元數N、NΔ及可分辨陣元數Nr

由于單個陣元在x或y正、負方向的分辨率不一定相同，由此得到的天線陣在正、負方向的分辨率也不一定相同，空間中的2個點在x或y方向是否可以分辨，需要比較兩點之間的距離與兩點在相互方向的分辨率.此時兩目標是否可分辨的評定準則為:如果兩目標點之間的距離大于相互方向分辨率的最大值，則兩點在圖像中可以分開;否則，一般情況下兩點之間不可分.即:假設空間中有2 個點目標 P(xp，yp)、Q(xq，yq)，假設 yp=yq，xp＜xq，則兩點在相互方向的分辨率分別為Δpx+、Δqx－，若xq－ xp≥max(Δpx+，Δqx－)，則兩點可以分辨;否則認為兩點不可分辨.為了方便與傳統的分辨率相比，可以定義系統在空間各點的距離向(y方向)及橫向(x方向)的分辨率分別為

2 仿真及結果驗證

2.1 分辨率的空間分布

假設接收天線為沿x軸均勻分布的線性天線陣，孔徑L=2 m，陣元數N=14.發射IR－UWB信號的時域分辨率為Tw=1 ns，自由空間下信號的傳播速度為v=c=3×108m/s.利用本文所提出的方法計算［－ 3，3］×［ 0，3］空間內各點分辨率如圖3所示，部分空間點的分辨率如表2所示.

圖3 天線陣各方向分辯率的空間分布

表2 部分點的分辨率

從圖3中可以看出，受近場條件的影響，距離向(y方向)分辨率在天線陣的近場區域中不再恒定，而是空間變化的，傳統的距離向分辨率計算公式在近場區域中不再適用.在天線陣附近，y方向的分辨率比較差，隨著目標到天線陣的垂直距離yp的增加，距離向的分辨率逐漸減小，并趨近于經典的遠場距離向分辨率cTw/2=0.15 m.而Δy－在天線陣附近比較小，是由于系統的成像區域限制在y＞0的區域而引起的(此時y方向分辨率的計算對應第一種情況).此外，由于對稱的天線陣對中心線兩側的作用相同，y方向的分辨率以x=0的直線(天線陣的中心線)鏡像對稱.隨著空間點逐漸偏離天線陣中心線，y方向的分辨距離逐漸增加.此時y方向的分辨率能力減弱，這是由于利用實孔徑天線陣對偏離天線陣中心線方向的目標進行成像時出現偏斜而引起的.

橫向(x方向)分辨率的空間變化相對比較復雜.受實孔徑及近場條件的影響，Δx+、Δx－在天線陣附近區域比較小，趨近于cTw/2=0.15 m，隨著yp的增加而逐漸增加.此外，由于天線陣是對稱的，Δx+與Δx－的空間分布之間關于天線陣的中心線對稱，Δx+、Δx－在中心線附近區域比較大，而在偏離中心線比較遠的區域，天線陣的橫向分辨率比較小，并且隨著目標的逐漸偏離，x方向的分辨率逐漸變小，并趨向cTw/2=0.15 m.其中Δx+在中心線的左側區域比較大，隨著x的減小先增加，當x減小到一定值時，由于用于確定分辨率的橢圓(e1、e2)發生了變化，Δx+突然減小到一個比較小的值，并隨著x的減小而逐漸減小;而在中心線右側區域，Δx+隨著x的增加而逐漸減小.

根據式(13)計算的空間各點橫向及距離向分辨率如圖4所示.從圖4中可以看出，橫向分辨率與距離向分辨率的空間變化趨勢近似相反，因此在實際的系統設計過程中，對系統參數的選擇需要考慮橫向分辨率與距離向分辨率之間的折衷.

圖4 距離向及橫向分辯率

2.2 分辨率結果驗證

根據1.2節中兩目標是否可分辨的評定準則，比較表2中所列的空間點之間的距離及相互方向的分辨率，可以發現，( 0，1.5)、(0. 64，1.5)兩點之間的距離小于相互分辨率的最大值，因此在圖像中應該無法分辨.而( 0，1.5)、(0. 67，1.5)兩點之間的距離大于相互分辨率的最大值，因此兩點目標在圖像中應該可以分辨.本節將利用數值仿真對本文所提出的分辨率計算方法進行驗證.

假設發射IR－UWB信號為理想的矩形脈沖，脈沖持續時間(即時間分辨率)Tw=1 ns.利用圖3中對應的天線陣對自由空間中位于( 0，1.5)、(0. 64，1.5)的 2個點目標進行探測成像，以－3 dB閾值對圖像進行分割得到的二值圖像及y=1.5 m時圖像的剖面圖如圖5(a)所示.同樣對 ( 0，1.5)、(0. 67，1.5)兩個點目標的成像結果如圖5(b)所示.從圖5中可以看出，雖然( 0，1.5)、(0. 64，1.5)兩點之間凹陷處信號小于峰值的－3 dB，但由于幅值小于－3 dB的距離很短，在二值圖像中兩點的圖像連接到一起，無法區分;而( 0，1.5)、(0. 67，1.5)兩點之間凹陷明顯小于峰值的－3 dB，在二值圖像中彼此完全可以分辨.與表2的分析結果完全一致，因此本文提出的分辨率的計算方法是有效的.

圖5 發射矩形脈沖時的成像結果

實際中，通常發射的IR－UWB脈沖為高斯脈沖或高斯脈沖的導數.文獻［15］指出對2個相同強度的理想信號來說，要區分它們并能精確測量它們的位置，兩個信號的間距必須大于等于－3 dB寬度的 2倍.因此取 Tw=2T－3dB，其中T－3dB為信號 －3 dB時間寬度.假設發射的 IRUWB信號為歸一化的高斯脈沖，即

脈沖的時間分辨率為Tw=2T－3dB=1 ns，對應的脈沖形成因子為α=1.066 3 ns，成像系統的其它參數不變，則對( 0，1.5)、(0. 64，1.5)兩個點目標以及( 0，1.5)、(0. 67，1.5)兩個點目標成像的結果如圖6所示.從圖中可以看出，兩種情況下的目標均可以清晰分辨，原本不可分辨的( 0，1.5)、(0. 64，1.5)兩點目標也可以很好的分辨.

圖6 發射高斯脈沖時的成像結果

對比圖5、6可以看出，對于實際發射的IRUWB信號，系統的分辨率優于矩形脈沖時的系統分辨率，這與文獻［9］中的結論一致.實際上，當發射脈沖時間分辨率相同時，本文提出的方法計算的分辨率對應著最差的分辨率，對于實際發射的信號波形，系統的分辨率會有不同程度的改善.但由于信號波形對分辨率的影響是全局性的，分辨率的空間總體變化趨勢保持不變，因此本文提出的分辨率計算方法對系統的設計具有重要的指導意義.

3 結論

IR－UWB近距離實孔徑成像系統中，窄帶、遠場的分辨率計算公式已經不再適用.本文基于理想的系統、點目標模型及BP成像算法的條件，通過對IR－UWB近距離成像原理的分析，推導了單天線的距離向、橫向分辨率的解析表達式，結合圖像重建過程中信號疊加原理，提出了利用實孔徑均勻線陣探測成像時，系統分辨率一種計算方法.并利用數值仿真驗證了該分辨率計算方法的正確性.

1)本文所提出的方法計算的分辨率對應著系統最差的分辨率，對于實際發射的信號波形，系統的分辨率會有不同程度的改善，但總體變化趨勢不變.相對于窄帶、遠場條件，受超寬帶、近場及實孔徑的影響，距離向分辨率不再恒定，距離向及橫向分辨率的空間變化更加復雜，橫向分辨率與距離向分辨率的空間變化趨勢近似相反，因此在實際的系統設計中，需要考慮橫向與距離向分辨率之間的折衷.

2)本文提出的分辨率計算方法，不但適用于對點目標的成像，而且適用于對復雜目標的成像［13］.利用本文的思想還可以計算近距離非相干成像、定位系統的空間分辨率.對IR－UWB近距離成像系統的設計具有重要指導意義.下一步工作將進一步分析分辨率與系統參數的關系.

［1］YAROVOY A G，SAVELYEV T G，AUBRY P J，et al.UWB array－based sensor for near－field imaging［J］.IEEE Trans on Microwave Theory and Techniques， 2007，55(6):1288－1295.

［2］ CHEN Lei，SHAN Ouyang.Through－wall surveillance using ultra－wideband short pulse radar:numerical simulation ［C］//Industrial Electronics and Applications，2007.ICIEA 2007.Piscataway:IEEE，2007:1551－1554.

［3］JOHN P F.Synthetic aperture radar［M］.New York:Spirnger－Verlag，1988.

［4］ MERRILL S.Radar handbook［M］.New York:McGraw－Hill Publishing Co，1990.

［5］楊延光，周智敏，宋千.分裂孔徑發射陣列接收BP算法方位分辨率分析［J］.信號處理， 2008，24(5):752－756.

［6］陳潔，方廣有，李芳.超寬帶穿墻雷達非相干成像方法［J］.中國科學院研究生院學報， 2007，24(6):829－834.

［7］ AHMAD F，AMIN M G.Noncoherent approach to through－the－wall radar localization ［J］.IEEE transactions on Aerospace and Electronic Systems， 2006，42(4):1405－1419.

［8］HUSSAIN M G M.Principles of Space－time array processing for ultrawide－band impulse radar and radio communications［J］.IEEE Transaction on Vehicular Technology， 2002，51(3):393－403.

［9］RIES S，KAISER T.Ultra wideband impulse beamforming:it is a different world ［J］.Signal Processing， 2006，86:2198－2207.

［10］KAISER T，ZHENG F，DIMITROV E.An overview of ultra－wide－band－systems with MIMO ［J］.Proceedings of the IEEE， 2009，97(2):285－311.

［11］粟毅.沖激脈沖SAR成像理論與方法研究［D］.長沙:國防科技大學，2001.

［12］呂彤光，陸仲良，粟毅，等.沖激信號SAR成像的方位分辨率分析［J］.電子學報， 2000，28(6):40－43.

［13］匡綱要.UWB雷達目標建模和信號設計［D］.長沙:國防科技大學，1996.

［14］盛衛星.微波成像技術及應用［D］.南京:南京理工大學，2001.

［15］WEHNER D R.High－resolution radar［M］.Norwood，MA:Artech House，1994.

［16］DESAI M D，JENKINS K.Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar ［J］.IEEE Trans on Image Processing， 1992，1(4):505－517.

Resolution of IR-UWB near-field real-aperture imaging systems

HUANG Dong－mei，ZHANG Qin－yu

(Shenzhen Graduate School，Harbin Institute of Technology，518055 Shenzhen，China，huangdongmei@126.com)

To solve the problem that the traditional“narrow－band，far－field”resolution formulas are no longer suitable for Impulse Radio Ultra－Wide Band(IR－UWB)real aperture imaging systems，a new algorithm to compute the resolution was proposed.On analysis of IR－UWB near－field imaging principle，the formulation of resolution in down－and cross－range for single antenna was derived.Combined with signal superposition in the process of imaging，an algorithm to compute the resolution for real－aperture uniform linear array was presented.Numerical simulation results of ideal point targets imaging verified the correctness of the algorithm.

resolution;IR－UWB;real－aperture antenna arrays;near－field;imaging

TN985

A

0367－6234(2011)09－0067－07

2010－04－05.

國家自然科學基金資助項目(60702034).

黃冬梅(1982—)，女，博士研究生;

張欽宇(1972—)，男，教授，博士生導師.

(編輯 張 宏)