刷密封刷絲力學行為與密封性能

王之櫟 郭苗苗 李理科

(北京航空航天大學 機械工程及自動化學院，北京100191)

刷密封中刷絲的變形能消除或減小由轉(zhuǎn)子徑向跳動等引起的密封間隙，因此被應(yīng)用于發(fā)動機旋轉(zhuǎn)件間的動密封，相對迷宮密封，其泄漏率可下降至后者的1/2～1/5，使推力/油耗比上升.刷絲尖端在轉(zhuǎn)子表面滑動，刷絲的力學行為以及接觸過程中產(chǎn)生的摩擦等是影響密封性能的主要因素.文獻［1］對刷密封中轉(zhuǎn)子與密封刷接觸扭矩進行了實驗測試;文獻［2］建立了刷絲變形的力學模型以及針對刷密封的磨損建模分析;文獻［3］就刷絲間摩擦力分布對滯后的影響以及轉(zhuǎn)子與刷絲間接觸力進行了研究分析;文獻［4］建立了基于CFD多孔介質(zhì)刷密封模型，在此基礎(chǔ)上對刷絲軸向和周向兩個方向的變形進行了研究.本文將對刷密封壓場和流場作用下的刷絲力學系統(tǒng)建立有限元模型，進而分析刷絲力學行為對密封性能的影響.

1 刷密封模型及實驗裝置

刷密封由緊密排列的金屬刷絲和用于固定刷絲束的前板和背板組成，刷絲在周向平面內(nèi)與轉(zhuǎn)子徑向呈一定傾角軸對稱排列，如圖1a和圖1b所示.圖1c為設(shè)計有長前板結(jié)構(gòu)與背板低滯后結(jié)構(gòu)的密封形式［5－6］.刷絲區(qū)域前的長前板，可以減小高壓氣體對前排刷絲的擾動，保持了其徑向壓緊“blow down”狀態(tài)，密封能力得以維持.當刷絲被壓緊時，將導致刷絲束間摩擦增大，柔性降低，跟隨性下降，尤其當轉(zhuǎn)子偏心運轉(zhuǎn)或瞬時侵入刷絲束并回復初始狀態(tài)時，刷絲不能立即隨之恢復與軸的貼緊狀態(tài)，而發(fā)生“hang up”，稱為滯后效應(yīng).圖1c所示背板低滯后結(jié)構(gòu)可以有效減緩滯后效應(yīng)的發(fā)生.根據(jù)密封刷環(huán)的特性，創(chuàng)建刷密封實驗臺如圖2所示.

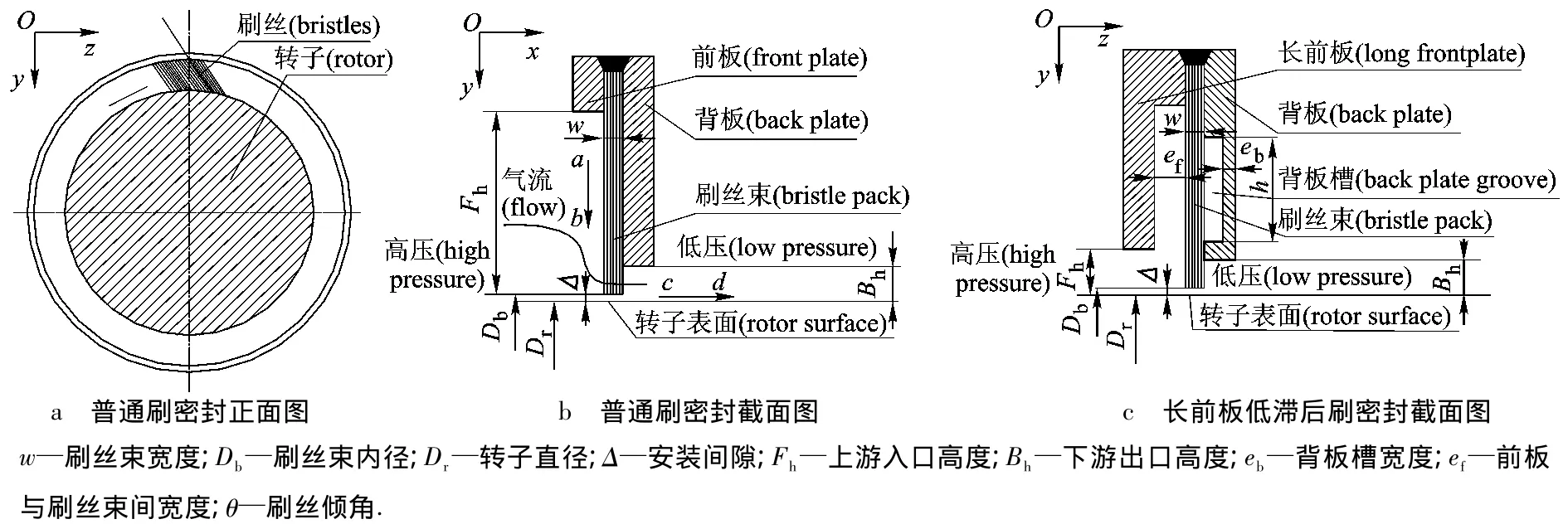
圖1 刷密封幾何結(jié)構(gòu)圖

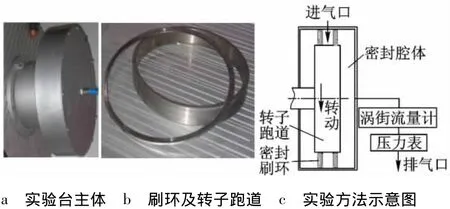
圖2 刷密封實驗臺

2 刷密封設(shè)計分析計算模型

2.1 流場計算模型與算法

刷密封壓力場的研究是研究刷絲力學行為的基礎(chǔ).由于密封具有軸對稱結(jié)構(gòu)，截取二維計算區(qū)域如圖3所示，采用自主開發(fā)的刷密封軟件Field CAL(以下簡稱Field CAL)借助多孔介質(zhì)模型，引入各向異性的阻抗力來表示刷絲區(qū)域?qū)α黧w的阻抗作用，將流體的控制方程組在流場區(qū)域離散，應(yīng)用“修正的解壓力耦合方程的半隱式算法”——SIMPLER算法迭代求解［7］.計算流場的控制方程組為

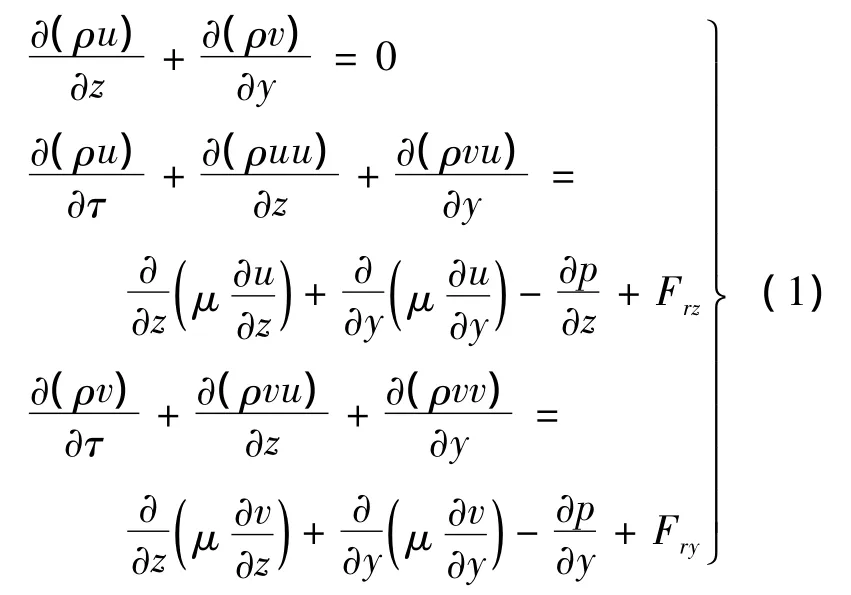
式(1)由質(zhì)量守恒方程和動量守恒方程構(gòu)成.其中，ρ為氣體密度;u，v分別為x軸和y軸方向氣流速度;τ為時間;μ為氣體粘度;p為氣體壓力;單位體積內(nèi)刷絲對流體的阻抗力［8］為

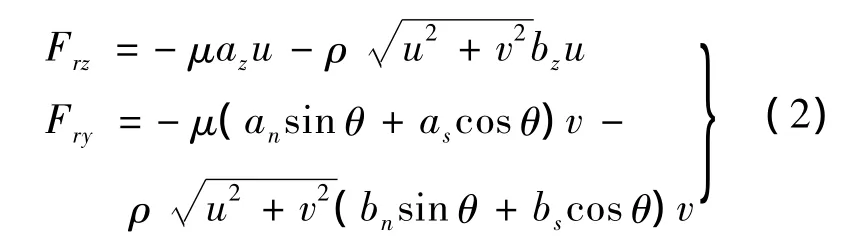
其中，az，an和 as分別為沿 z軸方向、x-y平面內(nèi)垂直刷絲方向和沿刷絲方向的粘性阻抗系數(shù);bz，bn，bs分別為相應(yīng)方向上的慣性阻抗系數(shù).無刷絲區(qū)域流場的阻抗系數(shù)為0.

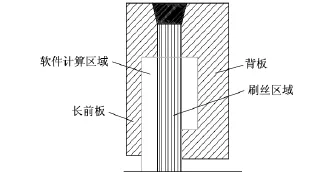
圖3 刷密封計算區(qū)域

計算密封區(qū)域壓力值后，根據(jù)刷絲在流場中的初始位置，可分別得到x-y平面和y-z平面內(nèi)單根刷絲各節(jié)點x向和y向壓差及流場對刷絲的作用力.

2.2 刷絲有限元模型

考慮壓力對刷絲作用、刷絲和轉(zhuǎn)子之間接觸力、刷絲之間以及刷絲與背板之間作用力，采用懸臂梁理論對系統(tǒng)進行有限元求解，計算出刷絲受力和變形及轉(zhuǎn)子所受摩擦扭矩.

2.2.1 刷絲受力分析

在周向-徑向平面內(nèi)以刷絲固定端為原點建立y軸、z軸;轉(zhuǎn)子軸線方向為x軸.刷絲與y軸呈一定傾角θ在圓周內(nèi)對稱安裝.x-y平面內(nèi)氣體從高壓側(cè)流向低壓側(cè).

x-y平面和y-z平面內(nèi)刷絲受力如圖4a、圖4b所示.為便于刷絲受力與變形分析，在圖4a中刷絲局部以其固定端為坐標原點、刷絲軸向為s軸、垂直刷絲軸向為t軸建立輔助直角坐標系.平面內(nèi)刷絲端部與轉(zhuǎn)子表面接觸力F=f(Ff，F(xiàn)n)，刷絲在流場中所受的氣體壓力Δqp由流場確定，刷絲之間存在相互作用力fi，圖4b中最后一排刷絲還受到背板作用力fb.

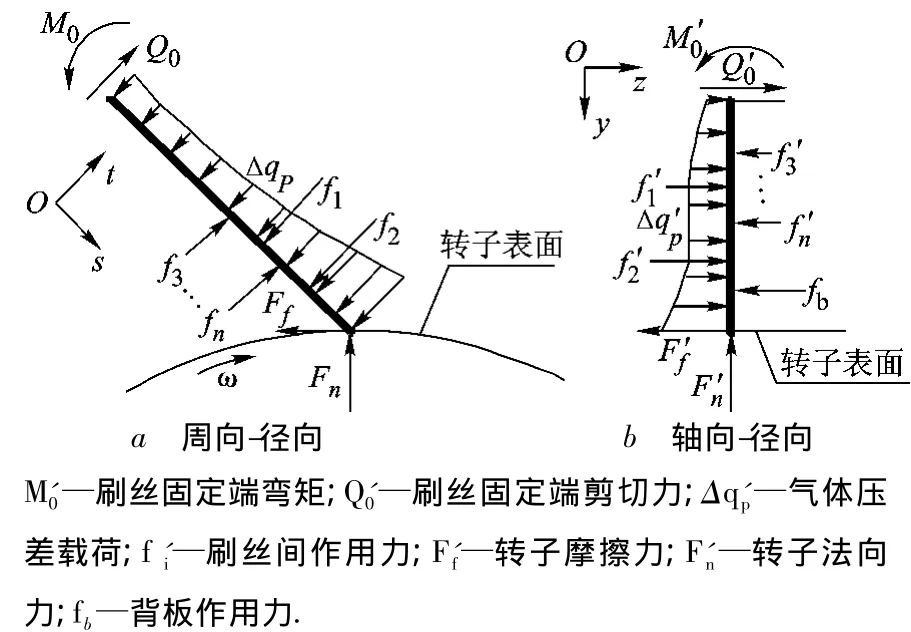
圖4 刷絲受力模型

2.2.2 刷絲有限元模型建立

根據(jù)刷絲受力和變形特點，將單根刷絲視為懸臂梁采用有限元法進行計算.

在圖4a中彎曲梁單元變形遵守伯努利-歐拉法則，有

其中，E為刷絲彈性模量;I為慣性矩;M為單元所受彎矩.

由懸臂梁彎曲理論可得未加載流場時由過盈安裝導致的刷絲端部法向力:

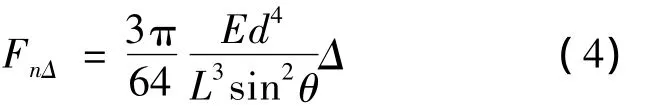
其中，d為刷絲直徑;L為刷絲自由長;Δ為過盈量;E為刷絲彈性模量.

在有限元模型中，每一根刷絲被分成k個小單元，因而在單元le內(nèi)，可將流場壓差視為均布載荷qe，得到流場中空氣動力產(chǎn)生的單元載荷矩陣:

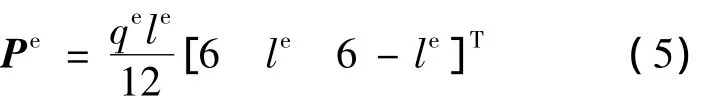
刷絲單元剛度矩陣:

綜合考慮刷絲與轉(zhuǎn)子接觸力和壓力，根據(jù)表征單元應(yīng)變和位移關(guān)系的幾何方程、應(yīng)力應(yīng)變關(guān)系對應(yīng)的物理方程可列出平衡方程，加載位移和力邊界條件，得到平衡方程的解，從而計算出節(jié)點受力和變形值.

刷絲變形位移邊界條件設(shè)定如下:

1)刷絲固定端節(jié)點橫向變形量.

2)刷絲端部節(jié)點橫向變形量.

由于刷絲變形為小變形，可認為刷絲端部平衡位置即為初始接觸位置，因此，刷絲與轉(zhuǎn)子間隙安裝條件下:

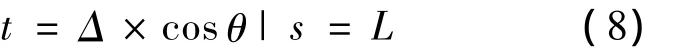
過盈安裝條件下:

t0為初裝時(未加載流場)刷絲端部變形量.

另外，在y-z平面內(nèi)計算刷絲變形時，位移邊界條件包括:刷絲固定端邊界;各排刷絲之間以及最后一排刷絲與背板之間存在最大允許位移.

3 計算結(jié)果及其分析

3.1 參數(shù)設(shè)置

刷密封設(shè)計分析軟件及實驗的刷密封結(jié)構(gòu)參數(shù)和主要工況參數(shù)設(shè)置如表1所示.

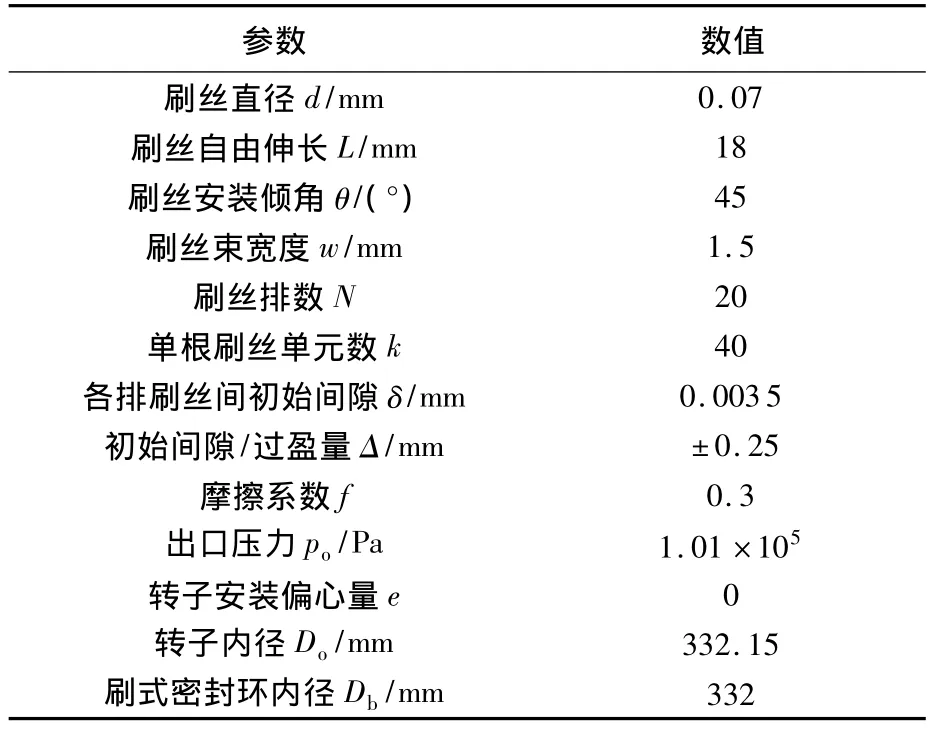
表1 刷密封主要計算參數(shù)

3.2 壓力場分布

刷密封中壓力場，y-z平面即軸向-徑向平面內(nèi)密封區(qū)域壓力分布見圖5，該區(qū)域內(nèi)y軸和z軸方向分別存在徑向和軸向壓力梯度，下游出口處壓力梯度最大.背板槽中產(chǎn)生均布的壓力，避免高壓下的刷絲束緊密貼緊背板而導致跟隨性下降.由于x-y平面壓力分布視為軸對稱，因而根據(jù)圖5可得壓比1.5時x-y平面內(nèi)壓力分布.

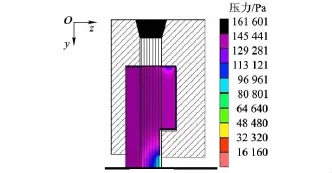
圖5 壓力場分布

3.3 刷絲變形

在得到壓力分布之后，就可以計算出壓力場中刷絲的變形情況.刷絲從高壓入口端到低壓出口端依次排列為第1排～第20排.

3.3.1 刷絲軸向-徑向變形

圖6為進出口壓比為1.5，安裝過盈量為0.075 mm的軸向-徑向變形圖.

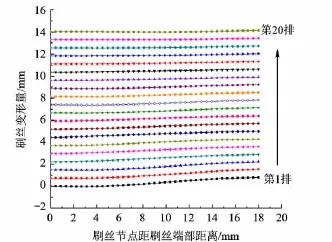
圖6 刷絲軸向-徑向變形

刷絲自由端在壓力梯度作用下變形較大，而最后一排受到背板的限制變形量相對較小.在軸向壓力的作用下，刷絲束整體向背板貼近.

3.3.2 刷絲周向-徑向的變形

安裝過盈量0.075 mm，進出口壓比1.5時的周向-徑向變形如圖7所示，由于初裝徑向彈力的作用下，刷絲束將沿徑向向外彎曲變形.在轉(zhuǎn)子旋轉(zhuǎn)時，刷絲受到轉(zhuǎn)子表面摩擦力Ff和法向彈力Fn與流體壓力共同作用，從而使刷絲端部貼近轉(zhuǎn)子，達到平衡狀態(tài).間隙安裝的周向-徑向刷絲變形如圖8所示，進出口壓比 1.5，安裝間隙為0.25 mm.

因壓場中靠近出口處的徑向壓降相對較大，后排刷絲變形大于前排，即較大的壓力降使得刷絲更貼近轉(zhuǎn)子以減小或閉合密封刷環(huán)初始安裝的間隙并減小泄漏量.

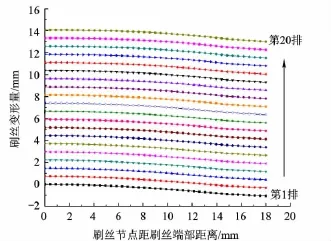
圖7 刷絲周向-徑向變形(過盈安裝)

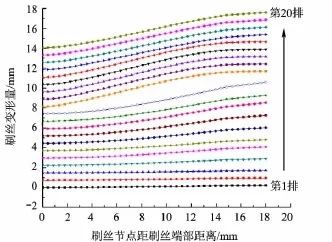
圖8 刷絲周向-徑向變形(間隙安裝)

比較圖7和圖8周向-徑向變形可知，間隙和過盈2種不同安裝形式下受刷絲與轉(zhuǎn)子間彈力與壓場徑向壓降共同作用下的刷絲變形達到平衡;受軸向流場的影響，間隙安裝時下游刷絲變形比上游的明顯偏大，上游可能形成縫隙;而過盈安裝時上下游各排刷絲變形接近，端部節(jié)點位移即為初裝位移量，此時刷絲端部均與轉(zhuǎn)子表面接觸.

3.4 性能分析

3.4.1 泄 漏 量

保持穩(wěn)定的低泄漏量是密封性能的重要評判標準之一.基于Field CAL的計算結(jié)果與實驗結(jié)果比較如圖9所示.

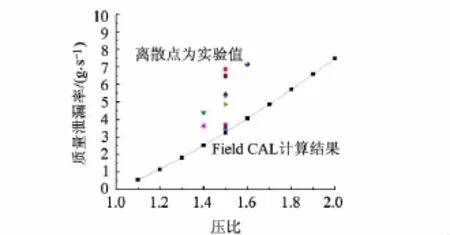
圖9 小壓比情況下的泄漏率對比

其中壓比范圍是1.1～2.0.相同壓比情況下的實驗值比程序值相對較大.Field CAL中使用阻抗力來代替真實刷絲對氣體的阻礙作用，阻抗系數(shù)取自文獻［4］.實際上密封刷中的刷絲束排列有的地方緊密有的地方稀疏，需綜合考慮阻抗系數(shù)的取值.

3.4.2 摩擦扭矩

摩擦扭矩是刷密封數(shù)值計算和實驗測量的關(guān)鍵參數(shù).基于流場中刷絲受力的計算，使用Field CAL可以計算出不同安裝狀態(tài)與不同工況下的摩擦扭矩.

圖10為Field CAL計算得出不同壓差，不同安裝過盈量下的刷絲端部與轉(zhuǎn)子之間摩擦扭矩值.摩擦扭矩隨著安裝過盈量的增大和壓差的增大而增大.表明壓力增大，壓力降使得刷絲更加緊密地貼近轉(zhuǎn)子，因而摩擦扭矩會隨之增大.

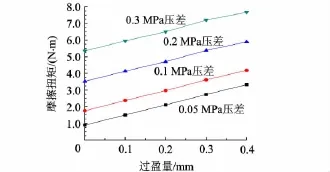
圖10 摩擦扭矩與過盈量關(guān)系曲線

圖11為實驗測試與Field CAL計算，沒有加壓力情況下不同轉(zhuǎn)速對應(yīng)的摩擦扭矩曲線對比，表明轉(zhuǎn)子低轉(zhuǎn)速變化時與摩擦扭矩關(guān)系不大.

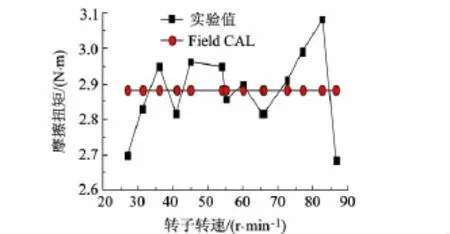
圖11 摩擦扭矩與轉(zhuǎn)子轉(zhuǎn)速關(guān)系曲線

4 結(jié)論

刷密封中流場分布和刷環(huán)與轉(zhuǎn)子安裝過盈量是影響刷絲系統(tǒng)力學響應(yīng)的關(guān)鍵因素.基于Field CAL計算的壓力場對刷絲受力與變形的計算，得到軸向-徑向和周向-徑向2個方向的刷絲變形量，并在此基礎(chǔ)上得到安裝過盈量和密封壓差與摩擦扭矩的關(guān)系.主要結(jié)論如下:

1)影響刷絲軸向-徑向平面內(nèi)受力和變形的主要因素是流場的作用，且由于靠近轉(zhuǎn)子壓力梯度較大，刷絲變形量較大;而背板的支撐作用使前排刷絲的變形量大于后排;

2)周向-徑向平面內(nèi)刷絲行為與安裝形式有關(guān).過盈安裝時，刷絲端部與轉(zhuǎn)子之間接觸力的作用使得刷絲彎曲變形;間隙安裝時，壓力梯度會使得刷絲貼近轉(zhuǎn)子使間隙閉合或減小;

3)作為刷密封實驗測量的主要參數(shù)之一，刷絲端部摩擦扭矩與安裝過盈量及密封兩側(cè)壓差均基本呈遞增關(guān)系，在刷密封設(shè)計中對于這些參量應(yīng)予控制，低轉(zhuǎn)速時，摩擦扭矩與轉(zhuǎn)子轉(zhuǎn)速關(guān)系不大;

4)Field CAL中阻抗系數(shù)的選取是能否準確模擬刷密封壓場與流場并計算其性能參數(shù)的關(guān)鍵因素之一.小壓比情況下的泄漏量的實驗測試值與Field CAL計算值的比較分析，為該工況下的阻抗系數(shù)選取和程序的修正提供了可靠的依據(jù).

References)

［1］Wood P E，Jones T V.A test facility for the measurement of torques at the shaft to seal interface in brush seals［J］.Journal of Engineering for Gas Turbines and Power，1999，121(1):160 －166

［2］Aksit M F，Tichy J A.Wear of brush seals:background and new modeling approach［J］.Tribol.Trans.，1998，41(3):368 － 374

［3］Zhao H，Stango R J.Role of distributed interbristle friction force on brush seal hysteresis［J］.ASME Journal of Tribology，2007，129:199－204

［4］Chew J W，Lapworth B L，Millener P J.Mathematical modeling of brush seals［J］.Int.J.Heat Fluid Flow，1995，16(6):493 －500

［5］Yahya Dogu，Aksit M F.Effects of geometry on brush seal pressure and flow fields—part I:front plate configurations［J］.Journal of Turbomachinery，2006，128:367 －378

［6］Yahya Dogu，Aksit M F.Effects of geometry on brush seal pressure and flow flieds—part II:backing plate configurations［J］.Journal of Turbomachinery，2006，128:379 －389

［7］王之櫟，梁小峰，宋飛，等.低滯后刷式密封數(shù)值分析［J］.北京航空航天大學學報，2008，34(9):1080－1083 Wang Zhili，Liang Xiaofeng，Song Fei，et al.Low hysteresis brush seal numerical situmulations［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(9):1080 － 1083(in Chinese)

［8］王之櫟，梁小峰，黃其武.刷式密封二維模型數(shù)值計算［J］.航空動力學報，2008，23(8):1461 －1465 Wang Zhili，Liang Xiaofeng，Huang Qiwu.Two-dimensional model mathematical stimulation of brush seals［J］.Journal of Aerospace Power，2008，23(8):1461 －145(in Chinese)