實現人臉圖像變形算法的研究

林 軍， 李新華

（安徽大學 計算智能與信號處理教育部重點實驗室，安徽 合肥 230039)

0 引言

數字圖像變形技術是在圖像中通過對控制點的位置改變而使整幅圖像產生理想變形[1]。常見的用網格扭曲、基于域圖像變形、非對稱經向基函數、基于小波變換等變形算法。圖像變形技術已在動慢、影視和醫學等領域都得到廣泛的應用[2]。

利用主動形狀模型特征點定位算法在一幅人臉圖像中提取 68個特征點，通過改變特征點位置對輸入人臉圖像進行剛性變形。

1 ASM人臉特征點提取

MPEG-4是世界上第一個基于對象(Object-based)的多媒體壓縮標準，人臉模型上定義了84個特征點,這84個特征點被分為若干組(如:臉頰、眼睛、嘴巴等)，如圖1所示。參考MPEG-4對二維人臉圖像定義了68個特征點，主要分布在外臉輪廓、眉毛、眼睛、鼻子、嘴巴上，這都是變形和動畫的主要部分。

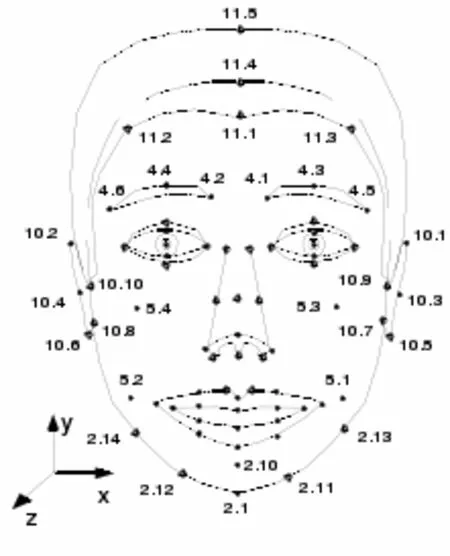
圖1 MPEG-4定義84個人臉特征點

ASM過程分2部分：①模型初始定位，也叫做形狀子空間模型；②搜索過程，搜索過程分 3步驟，分別為計算新位置、計算形狀和姿態參數更新[3]，特征點定位流程如圖2所示。

總體定位是指對輸入圖像的形狀進行歸一化處理，通過最小化目標函數得到特征點的最佳匹配向量。局部定位是指當面部圖像存在多個特征細節時，某些局部特征區域的特征點可能由于全局優化的作用而無法準確定位，因此經過全局模板搜索定位后，可以在全局定位的基礎上進行局部定位[4]。

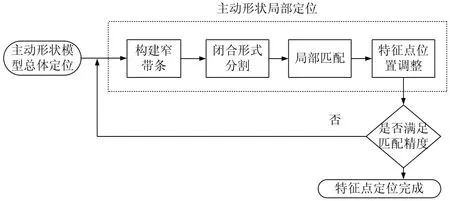
圖2 特征點定位實現

用ASM算法檢測到輸入人臉圖片68個特征點，如圖2所示。

圖2 ASM算法檢測68個特征點

2 人臉圖像剛性變形

移動最小二乘法是通過控制一些控制點或控制線來修改這些點的位置，根據變形函數來改變周圍像素點位置而使圖像產生變形效果，移動最小二乘法（MLS，Moving Least Squares,）理論模型[5]，存在變形函數f，使（1）式取最小值。

式中zi為權重，si為原圖控制點坐標。di為目標圖控制點坐標。變形函數f(p)可分線性換項和平移變換項：

將（2）代入(1),對的變量求導且等于零,求最小值：

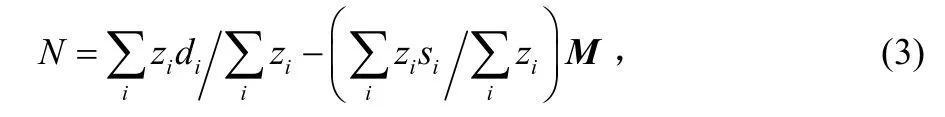
變形函數一般形式為：

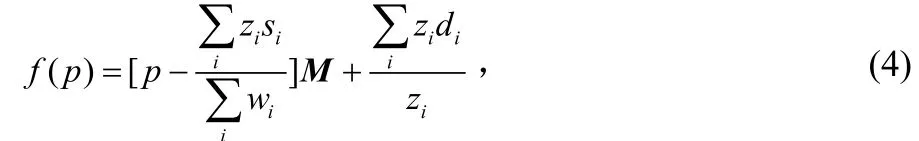
式(1)可為：

轉換矩陣M可以為仿射變換,相似變換和剛性變換,做剛性變換后，在保持原圖像角度關系上前面所用的相似變換的效果要優于仿射變換，但是某些局部位置的同比例縮放經常會產生不理想的效果。近來，許多科研人員表明對于真實的形狀而言，不但變形必須盡可能嚴格，而且變形的空間必須包括統一的縮放比例。傳統上圖像變形方面的研究者直接接近這個問題存在一定難度。對于真實感的形狀，在圖像變形過程中要進行變形時需要盡可能的保持剛性。限制M性質可以推倒出剛性變換函數[6]：

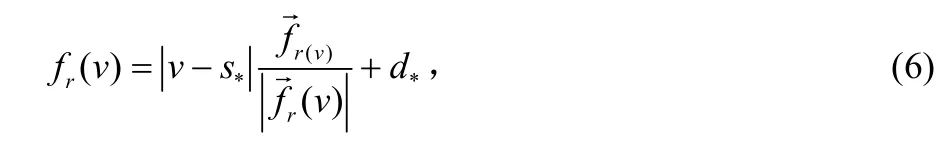
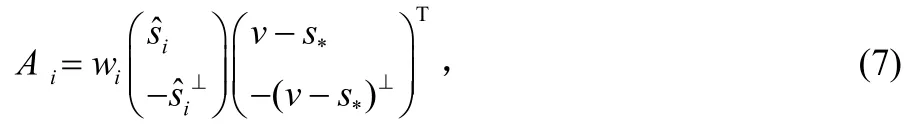
⊥ 為二維向量操作符(x,y)=(-y,x)⊥。

權函數也可以選擇4次樣條函數：

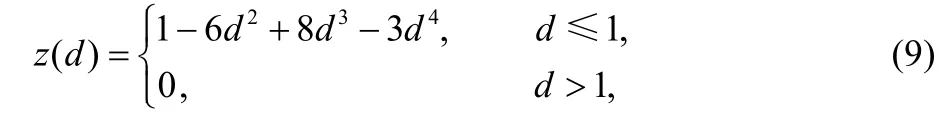
權函數選取還可以是Gauss函數、指數函數和三次樣條函數等。影響半徑決定影響區域大小，影響半徑越小，變形局部性就越好,影響半徑大，變形的局部性也越弱[7]。影響半徑R不能取任意小，否則可能導致變形函數不再一對一變形,圖像變形后會出現重疊奇異現象[8]。

3 實驗結果

在人臉局部變形中，本文設置了表情動作與面部重要特征點移動規則，分別有高興、驚訝、害怕等5種基本表情。

表1 表情動作對照表

人臉表情動作結合上節自動人臉特征提取68個特征點分布，列舉了高興表情變形，最左邊圖標出68個特征點，中間一幅為改變某些特征點位置后的圖像，最右邊為變形后圖像。

圖3 人臉圖像剛性變形

4 結語

經過實驗效果可以看出，主動形壯模型（ASM）算法進行特征點提取，用特征點作為控制點，運用改進的移動最小二乘法對圖像進行剛體變換，操作簡單，控制點容易操作，便于實現，圖像變形平滑，真實感強，理論和實踐證明此方法可行性強，值得考慮的是在以后研究中做到系統化和可視化。

[1]鮑虎軍. 計算機動畫的算法基礎[M]. 杭州: 浙江大學出版社,2000:23-34.

[2]王章野, 金小剛. 圖象變形綜述[R]. 浙江大學, 2004.

[3]DANA H, CHRISTOPHER M. Brown Computer Vision[M]. Prentice Hall, 1982:56-63.

[3]WOLBERG G. Digital Image Warping[M]. Los Alamitos:IEEE Computer Society Press, 1990:124-133.

[4]LAZARUS F, VERROUST A. Three-dimensional Metamorphosis:a Survey[J]. The Visual Computer, 1998, 14(09): 373-389.

[5]WENG Y L, WU Y C. 2D Shape Deformation Using Nonlinear Least Squares Optimization[J]. The Visual Computer, 2006, 22(09):653-660.

[6]SCHAEFER S, MCPHAL T. Image Deformation Using Moving Least Squares[J]. ACM Transactions on Graphics, 2006, 25(03):533-540.

[7]孫家廣. 計算機圖形學[M]. 北京: 清華大學出版社, 2005:31-44.